基于类内均方偏差的无监督领域自适应

李嘉豪，蔡瑞初

（广东工业大学计算机学院，广州510006）

0 引言

随着社会和科技的发展，人类的活动数据与日俱增。由于数据处理远不如数据生成高效，各个领域都亟需一种高效的学习方法来处理大量堆积的无标签数据。大量的研究工作表明，这种问题能够被无监督领域自适应算法[1]有效解决。这种算法能够把源领域的类别信息迁移到无标注的目标领域中，避免了繁重的标注工作。

目前，分布对齐思想被主流的无监督领域自适应算法所采用。一些算法假设目标领域总体分布是源领域总体分布的一个子集，并试图对样本重加权或挑选以抽取出一个符合目标领域特性的分布[2-4]。一些算法假设目标领域总体分布是源领域总体分布的一个低维映射，并试图挑选与领域弱相关的局部特征来对齐领域的低维总体分布[5-7]。这两种分布对齐方法可以混合使用。最简单的方法是使用两个投影矩阵分别加权源领域和目标领域的全体数据集，然后使用一定的策略约束投影矩阵和加权结果的相似性[8-9]。为了使投影矩阵能够对齐领域总体分布或条件分布，算法需要引入再生核希尔伯特空间，并执行核对齐准则[10-11]和分散准则[12-13]。

然而，浅层模型没有为算法提供一个充足的用于分布对齐的参数空间，算法在面对更为复杂的场景时无法挖掘出足够的高层分类知识。为此，不少研究工作使用深度学习来完成无监督领域自适应任务。部分工作会从神经网络中划分一个特征提取器，然后使用最大均值差异对齐不同领域的特征分布差异[14-15]。此外，一些研究工作表明，在基于多任务学习思想设计的神经网络上，对目标领域重构误差最小化或对领域判别误差最大化，能够帮助算法寻得领域一致的类别空间。两个领域的特征分布还可以通过对抗学习[20]的形式进行对齐。通过反转领域判别器到特征提取器的梯度，特征提取器能够去除源领域和目标领域中的领域专用信息[21-22]。此外，两个共享权重的生成对抗网络也能够对齐生成器的输出特征分布[23-24]。

不过，这些深度算法经常造成分布差异和分类误差互相抗衡的局面。该问题主要由总体分布对齐引起的，因为从对齐的总体分布中得到的知识未必就是有效的类别信息，从而无法保证类别信息的有效利用。为此，所提算法使用类内均方偏差（Intra-Class Mean Square Bias）准则对齐两个领域的类内分布。这种做法会通过模型预测所有领域样本的伪标签，然后对齐两个领域中带相同伪标签的数据分布。这种做法能够最大限度保留源领域的类别信息，并且有效减少源领域中某些专用类别信息的干扰。实验结果表明所提算法能够通过类内均方偏差准则有效对齐两个领域的类内分布，并得到了最佳的性能表现。

本文接下来引入一个风险上界，并以此概括无监督领域自适应算法的设计理念，然后从风险上界中引出基于类内均方偏差的无监督领域自适应算法。最后把所提算法与一系列对比算法进行比较，以验证本文所提算法的效果。

1 无监督领域自适应

领域自适应能够被一个风险上界所描述。在给定转换函数g 后，这个风险上界能够被拆分为两个部分。第一部分为目标领域的后验分布pT(Y|g(X))与源领域的后验分布pS(Y|g(X))之间的差异。第二部分为源领域的后验分布pS(Y|g(X))与经验模型的后验分布q(Y|g(X))之间的差异。这些分布差异可以定义为L1距离，即给定任意转换函数g 和领域D ∈{S,T}后，后验分布p(Y|g(X))和q(Y|g(X))之间的差异被定义为：

定理1 如果给定转换函数g 和源领域S 后，源领域的后验分布pS(Y|g(X))与经验模型的后验分布q(Y|g(X))之间的差异被量化为ϵS( )g,q,pS，那么同理可得，并且有不等式：

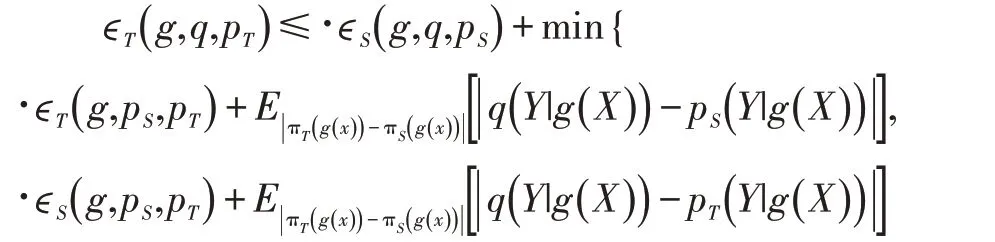
由定理1 知，若目标领域的后验分布pT(Y|g(X))与源领域的后验分布pS(Y|g(X))之间的差异Δ 足够小，那么对齐源领域的后验分布pS(Y|g(X))与经验模型的后验分布q(Y|g(X))才有意义，因为q(Y|g(X))能够逼近pT(Y|g(X))。不过，若使用有监督模型来拟合源领域的后验分布，那么q(Y|g(X))逼近pT(Y|g(X))的程度有限。因为Δ 无法得到优化。为此，无监督领域自适应任务会借助目标领域中的无标签样本最小化Δ，从而使q(Y|g(X))进一步逼近pT(Y|g(X))。根据Δ 的形式，对齐两个领域的总体分布πS(g(x))和πT(g(x))能够达到最小化Δ 的效果。于是，无监督领域自适应算法有两个任务：①使用任意的有监督模型来拟合源领域的后验分布；②使用一个评估函数量化并对齐两个领域的总体分布差异。

2 类内均方偏差准则

根据上一节的讨论，算法需要借助评估函数对齐领域总体分布πS(g(x))和πT(g(x))。一种有效的评估函数是均方偏差准则，即MSB（Mean Square Bias）。它的定义如下：

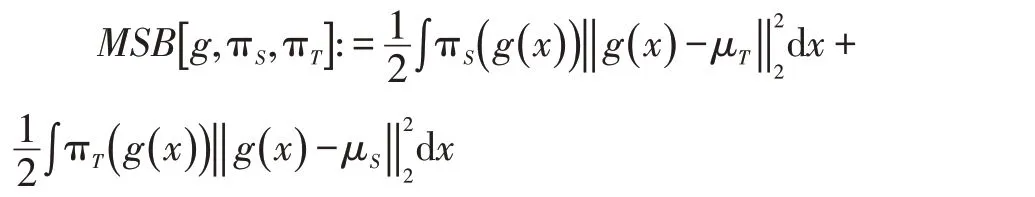
其中，μS和μT分别为g(x )在两个领域上的期望。为了在数据集上评估分布差异，均方偏差准则有经验评估：

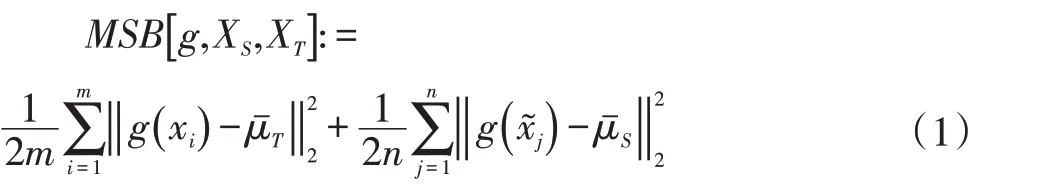
然而，定理1 表明，如果算法使用均方偏差准则对齐总体分布，那么模型可能无法避免分类信息的流失。由于模型与源领域的后验分布差异还影响到后验分布差异Δ，对齐领域总体分布有可能造成经验模型的后验分布无法逼近源领域的后验分布，从而增大后验分布差异Δ。为此，算法转而对齐两个领域的类内分布。根据式（1），针对类别c 的均方偏差可以定义为：

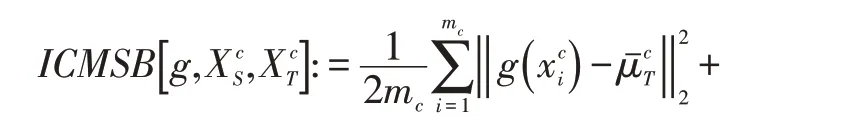
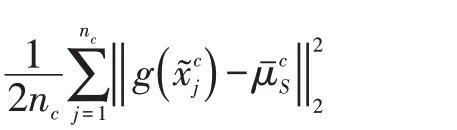
3 具体模型及算法

综合上述讨论，基于类内均方偏差的无监督领域自适应算法有以下目标函数

其中，损失函数L 采用均方误差或Softmax 函数等。超参λ 决定ICMSB 正则项的误差贡献程度。

根据式（2）的目标函数形式，算法有两个任务。第一个任务是对分类器f 和特征提取器g 进行优化，从而最小化源领域分类误差。第二个任务是对特征提取器g 使用ICMSB 进行优化，从而对齐类内分布。这里需要说明一点，为了减少内存占用，算法在每个迭代I最小化以下形式的ICMSB 正则项。

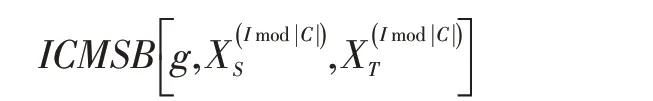
其中，集合C 代表两个领域的类别空间。

考虑到目标领域的类别空间在无监督场景下无法被访问，并且源领域和目标领域都存在领域专用的类别信息，因此输入到ICMSB 正则项的样本都带有伪标签。除此之外，考虑到未收敛模型的弱分类能力会造成某类伪标记样本不够充足，因此算法需要对伪标记样本进行过采样。整个过采样流程主要由阈值τ 和α控制。详细地说，当两个领域的同类伪标记样本个数都不低于τ 时，算法分别对采样α 次。否则，算法分别对原始数据XS和XT采样α 次。总之，无论哪种采样方式被算法执行，这套过采样流程都会额外产生两个样本集和。最后，为了保证模型收敛，所提算法计算以下梯度缩放率。

基于上述目标函数的形式，神经网络结构的设计如图1 所示。整个算法流程有四个步骤。第一步预测两个领域中所有样本的伪标记。第二步对伪标记样本执行过采样流程，并得到第三步评估类内分布差异和分类误差。第四步更新并学习分类器f 的参数θf和特征提取器g 的参数θg。这些参数的更新幅度由学习率η 控制。

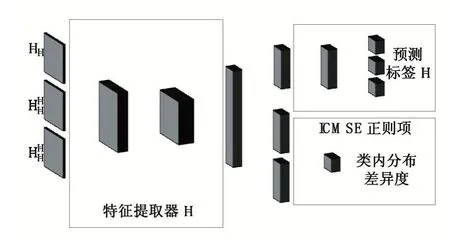
图1 神经网络结构

综上所述，基于类内最大均方偏差的无监督自适应算法有以下训练过程：

（1）对于当前迭代I：

（2）c ←I mod|C|

（4）mc←0，nc←0

（5）对于每个下标i=1,2,…,m，若xi带有伪标签c：

（7）对于每个下标j=1,2,…,n，若x˜j带有伪标签c：

（9）如果mc≥τ 并且nc≥τ：

（11）否则，分别从XS和XT中采样α 次，得到和

4 实验配置及结果

为了比较所提算法与主流算法，本文采用精度（Accuracy）指标来量化所有算法的性能表现。由于使用神经网络对目标函数进行建模，所提算法被部署到CAFFE[25]深度学习框架中。

考虑到对比实验的公平性，所有实验均使用OFFICE-31 图片数据集①下载地址为https://pan.baidu.com/s/1o8igXT4#list/path=%2F。OFFICE-31 包含三个领域，分别为AMAZON、DSLR 和WEBCAM。这些领域都包含31 种类别的图片。其中，AMAZON 包含2817 张图片，DSLR 包含498 张图片，WEBCAM 包含795 张图片。考虑到OFFICE-31 的数据形式，所有算法都在六种领域自适应场景中验证它们的有效性。这六种场景分别为‘A2W’、‘W2A’、‘A2D’、‘D2A’、‘W2D’和‘D2W’。其中，‘2’之前的字母代表源领域，剩余的字母代表目标领域。

为了更好地展示所提算法的优越性，实验选用了四个主流对比算法，分别为GRL[18]、DRCN[16]、DAN[15]和DDC[14]。其中，GRL 通过最大化领域预测错误率来寻找一致的类别空间，DRCN 借助自动编码器对齐隐层特征的类别空间。DAN 和DDC 均采用最大均值差异（Maximum Mean Discrepancy，MMD）对齐领域分布，其中前者使用单核MMD，后者使用多核MMD。

同时，所有算法的网络骨架均采用AlexNet[26]，见图2。对比算法中的正则项及超参数维持原论文公布的设计。所提算法的正则项采用ICMSB 的设计，并受四类超参数控制。第一类超参数是初始学习率η0及其退火策略，主要控制模型的迭代优化量。由于OFFICE-31 数据集充满背景噪声，为了不影响模型收敛，算法采用初始学习率较小的退火策略来调整学习率，即η0被设为0.001，并在每个迭代I 计算以下学习率η。

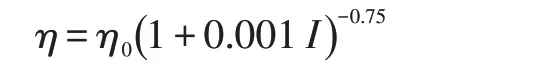
第二类超参数是迭代周期数，主要控制模型的更新次数。由于使用了较小的学习率，算法把迭代周期数设定为50000，即I 的取值不能超过50000。根据设定，算法使用随机梯度算法对模型中的所有参数更新50000 次。第三类超参数是正则项权重λ，主要影响正则项对整体目标函数的误差贡献。由于ICMSB 自带缩放功能，正则项权重λ 被设定为1.0。第四类超参数是阈值τ 和α，主要控制算法的过采样逻辑。在本文实验中，它们被设定为7 和64。亦即，当两个领域都有7 个同类伪标记样本时，算法对这些样本采样64 次。

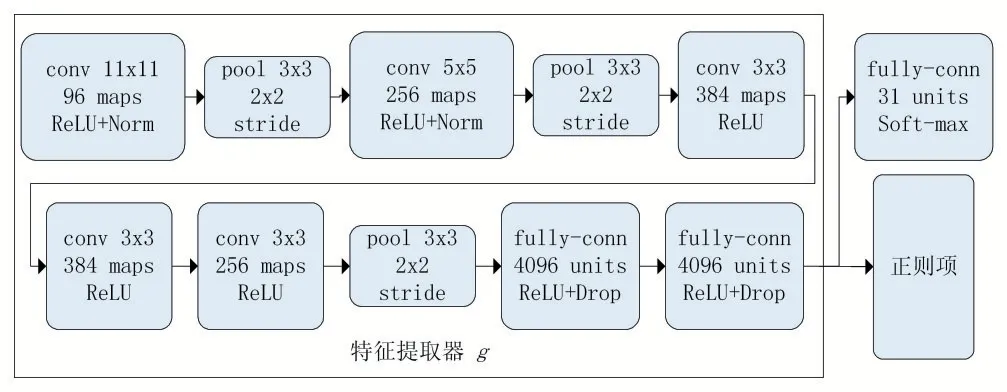
图2 具体网络结构

在OFFICE-31 数据集上，将所提算法与GRL、DRCN、DAN、DDC 相比较，并得到以下实验结果。

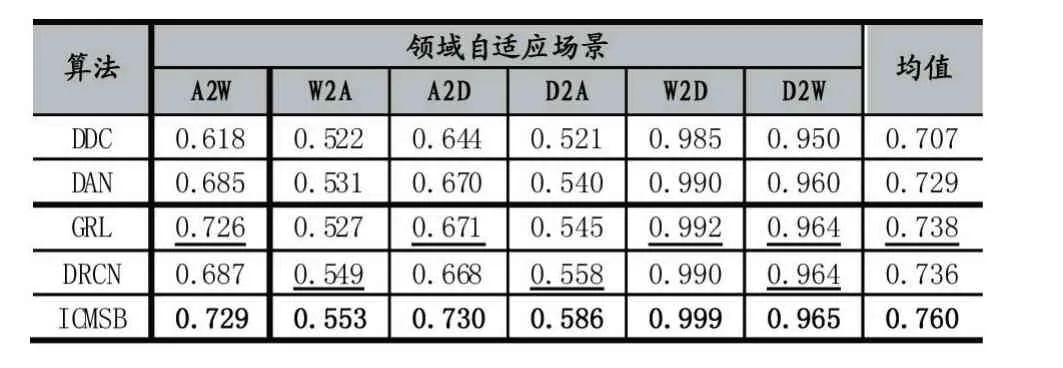
表1 OFFICE-31 上的算法精度比较

由表1 可知，在所有的领域自适应场景下，ICMSB的精度都高于主流算法。这是因为ICMSB 只对齐两个领域的类内分布，避免了传统算法的类别信息流失问题。由于其他算法在对齐总体分布时总是过多地流失类别信息，这些对比算法的实验精度都不及ICMSB。显然，对齐总体分布会削弱模型对目标领域的预测能力。

值得说明的是，所有算法在‘W2D’和‘D2W’自适应场景中都有良好的表现。这是因为DSLR 和WEBCAM 的原始数据分布是十分接近的。此外，GRL 和DRCN 分别在‘W2A’和‘A2W’场景中表现远远不及ICMSB，但GRL 和DRCN 分别在‘A2W’和‘W2A’场景中表现接近ICMSB。这表明对齐总体分布不一定流失太多的类别信息。此外，在所有自适应场景中，DAN 的精度都高于DDC。这表明多核MMD 能够有效保留源领域的类别信息。

5 结语

针对传统算法的类别信息流失问题，本文提出了一种基于类内均方偏差的无监督领域自适应算法。这个算法能够对齐不同领域的类内分布。得益于这种类内分布对齐的设计，算法有效保留源领域中具备迁移能力的类别信息，从而获得优于主流算法的性能表现。