声学多普勒测速仪标校技术研究

乔梓航，朱安珏，杨蕊



声学多普勒测速仪标校技术研究

乔梓航1,2，朱安珏1，杨蕊1,2

(1. 中国科学院声学研究所东海研究站，上海 201815；2. 中国科学院大学，北京 100049)

为了提高声学多普勒测速仪输出速度的准确度，安装过程中测速基阵与载体之间的偏差角不可忽略，安装偏差角包括航向偏角，横摇角及纵摇角三类。介绍了一种三维空间上的多普勒标定技术，通过高精度的GPS导航仪以及多普勒测速仪对海底测速，利用速度比值差校准航偏角。通过纵向剖面的几何关系，从航偏角出发进而获得纵摇角和横摇角的大小，完成了三维方向上多普勒测速仪的校准，使多普勒测速仪坐标系与载体坐标系能够进行精确转换，从而提高了声学多普勒测速仪输出速度的准确度。外场试验较好地证明了该方法的有效性，分析结论看出在二维平面上，造成误差的原因主要在于安装偏角的航向偏角，而在三维空间上，尤其垂向速度，误差主要由纵摇角和横摇角产生。该方法可以快速地对三维安装偏角进行校准，运算量小，并且在对海水测速后续研究中可以形成一套体系。

声学多普勒测速仪；安装误差校准；三维空间校准；速度比值法

0 引言

船载多普勒测速仪通过对多普勒频移信息进行解算进而得到对海水或者对海底的速度信息，进一步可以得到载体航速、航迹等信息。相比于全球定位系统(Global Positioning System, GPS)需要利用卫星定位，多普勒测速仪可以自主得到航迹航速，在进行水下探测时具有GPS所没有的优势。

测速仪的主要误差在于基阵安装时的安装偏角，无论人为如何精确地对准，包括前期的基阵设计和后期的基阵安装，测速基阵总会与载体艏向、横向和纵向间存在安装误差，该误差从空间上看是三维的误差，即与载体艏向误差、载体横向误差以及载体的纵向误差[1-3]。在安装时，我们希望GPS导航仪、姿态传感器和测速基阵的坐标系在空间上全部对齐，但是安装误差会以恒定偏移的形式添加到解算的载体速度上，从而使得画出的航迹路线与实际航迹偏离得越来越远。虽然安装误差角度较小，并且下文可以看到的横摇偏差和纵摇偏差对载体运动的影响远小于航偏误差，但是使用多普勒测速仪估计对水速度时，偏移误差就显得非常重要，0.1°的纵摇误差会让船体运动的0.5%变成垂直分力，0.1°的航偏角误差会让船体运动的0.5%变成侧向分力。偏差速度与船体运动速度相比较小，但是当研究对水速度时，由于水的运动速度通常比较小，而安装的误差保持不变，对水流测速的影响就会越来越大。本文将介绍如何利用多普勒测速仪的对底测量速度校准航偏角，通过和GPS的航迹比对，得到测速基阵安装的航偏角。再利用纵向剖面的几何关系，进一步校准横摇偏角和纵摇偏角。

1 三维空间校准

1.1 航偏角校准

首先对航偏角与横摇角和纵摇角做出说明：载体行驶时与大地坐标系下正北方向的夹角为航偏角；水平方向上，载体纵倾与水平面的夹角为纵摇角；载体横摇时与水平面的夹角为横摇角，此为普遍意义上的定义。而在研究多普勒测速仪时，航偏角、纵摇角和横摇角的定义如下：安装时多普勒测速仪与载体之间存在安装偏角，与载体艏向的夹角为航偏角，与载体纵向的夹角为纵摇角，与载体横向的夹角为横摇角。如果想使用船与大地的夹角，应说明由姿态仪获得的航偏角、纵摇角和横摇角[6]。而本文中说的航偏角纵摇角和横摇角泛指安装时测速仪与载体之间的偏角。测速基阵、载体和大地位置如图1所示。

图1 测速基阵、载体和大地之间的位置关系

从航偏角角度来看，从基阵坐标系到船体坐标系有：

图2 三种坐标的转换关系

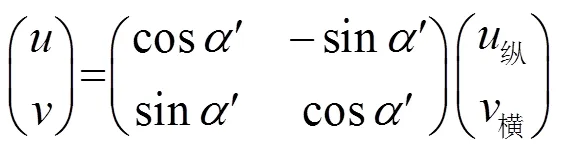
从船体坐标系到大地坐标系有

理想情况下我们希望GPS、姿态仪和测速基阵在同一点处，并且保持刚性连接，这样可以减少船航行时晃动的随机误差。考虑安装偏移的纵、横摇角度时，有：

其中，为纵摇安装偏角，为横摇安装偏角。文献[1]提出的最小二乘法用比较精确的方法计算航偏角，但求解时往往不满足旋转矩阵求解条件：

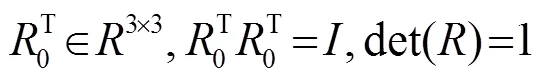
文献[2]令横摇角、纵摇角的值先为0，进而求解航偏角，然而实际横摇和纵摇角不为0，从而校准的航偏角存在先决条件上的误差，尽管在二维平面上，纵、横摇角度对航偏角的影响较小，但是没有三维校准还是无法补偿纵、横摇角度对航偏角的影响。而采用航速比值法可以快速地测得航偏角进而对横摇角和纵摇角进行校准，进一步的纵、横摇角度校准可以补偿其对航偏角的影响，并且计算量小、实现简便。多普勒测速仪的方向可以用其得到的对底横向和纵向的速度比值得到，以GPS的数据作为参照，可认为是准确数据，因此，由GPS得到的横向和纵向速度的比值与多普勒测速仪的横向和纵向速度比值的差值就是实际的安装偏角：

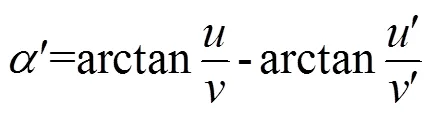
该方法可以有效地得到航偏角，因为将GPS看为准确的参考系统，所以该航偏角的主要误差取决于GPS的精度。因此船载需要高精度的GPS来尽可能地满足航偏角的校准要求。该方法只适用于可以对底进行测速的多普勒测速仪。

1.2 横摇角、纵摇角校准

设定多普勒测速仪的波束线与法线的夹角为，为一个确定值，4个波束的斜距为1，2，3，4，和分别为多普勒坐标系的横轴和纵轴。考虑波束1、2的所形成的剖面，设海底较为平缓，对底深度可以探测，纵向剖面示意图如图3所示。

图3 纵向剖面示意图

图3中，角12为多普勒测速仪坐标系与水平面的夹角[4-5]，易得：

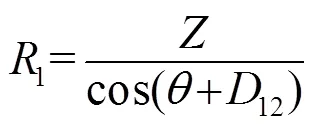
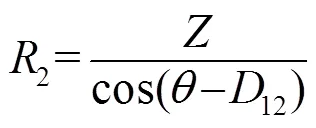
由式(6)、(7)可知：

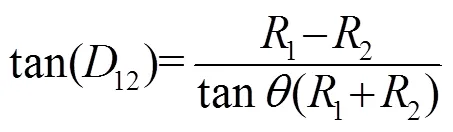
同理，考虑波束3/4形成的剖面，得到：

现在已经得到航偏角、横摇角和纵摇角的安装偏角、、，行船姿态角由船载姿态仪获得，设角度为、、，因此实际由多普勒测速仪测得速度为[8-9]

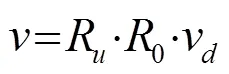
通过式(12)可以得到校准后的速度，由此将多普勒测速仪速度经过两次坐标变换，使测得速度从开始的多普勒坐标系转换到大地坐标系，实现了安装偏角的校准，提高了可使用速度的准确度。

2 试验验证分析

试验使用自研中心频率为75 kHz的多普勒测速仪，GPS采用Navcom的SF-3050，可以提供实时厘米级的定位精度，姿态仪采用的是Octans光纤陀螺仪，精度能保持在航向0.1°，纵向0.01°。于某试验场进行了试验，航速设定为4 kn，安装图示如图4所示，船体长13 m，宽度4 m，试验湖域的水深在46 m，上下浮动2 m，湖面平静未遇到较差水况，船体可以保持某一速度匀速行驶。接收到的GPS信息视为精确数据，由GPS可以画出行船轨迹。姿态仪固定于船上，提供船体的姿态信息。

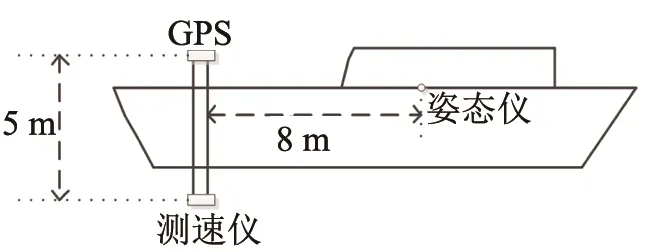
图4 安装位置示意图

图7为二维平面航迹平均速度法校准对比图。由图7可知，与传统的平均速度法相比，速度比值法在二维平面上得到了更好的校准效果，并且进一步可以提供三维方向的校准，而平均速度法仅仅局限于二维平面的校准，由于平均速度法需要直线平稳的航行条件，所以无法对弧线的航迹做出校准。

图5 三维空间直线航迹

图6 二维平面直线航迹

图7 速度比值法与平均速度法校准的二维平面航迹对比图

弧线航迹图如图8～9所示。

由图8～9的航迹图可以看出：即使前期人为的设计和安装尽量减小多普勒测速仪的安装偏差，仍然存在较大的误差，通过三维校准方法可以有效地减小安装偏差。主要存在安装偏差的是航偏角，航偏角校准后，二维平面上可以看出行船轨迹向GPS航迹发生最明显的偏移和靠拢，而横摇和纵摇安装偏角对多普勒测速仪解算的航迹在二维平面上的影响不如航偏角大，但在三维空间看，不进行纵摇和横摇角度的校准会使行船轨迹向下方延伸，并且随着行船距离的增加，误差也逐渐增大。

图8 三维空间弧线航迹

图9 二维平面弧线航迹

行船轨迹是弧线时，误差累积比直线航行大，在三维图可以看出轨迹螺旋向下，即从二维图来看，载体没有过多偏离航迹，但在三维空间上和实际情况严重不符，经过三维空间上的校准后，可以看出行船轨迹基本回到了一个稳定的平面。

从图10～15的误差图中可以更直观地看出校准前后的变化。

直线航行时，横向位移、纵向位移、垂向位移误差的误差图如图10～12所示。弧线航线时横向位移、纵向位移、垂向位移误差如图13～15所示。

从误差图可以看出：

(1) 人为安装确实存在安装误差，并且安装误差较大。安装偏角所造成的测速误差会使行船距离偏离实际航线越来越远。

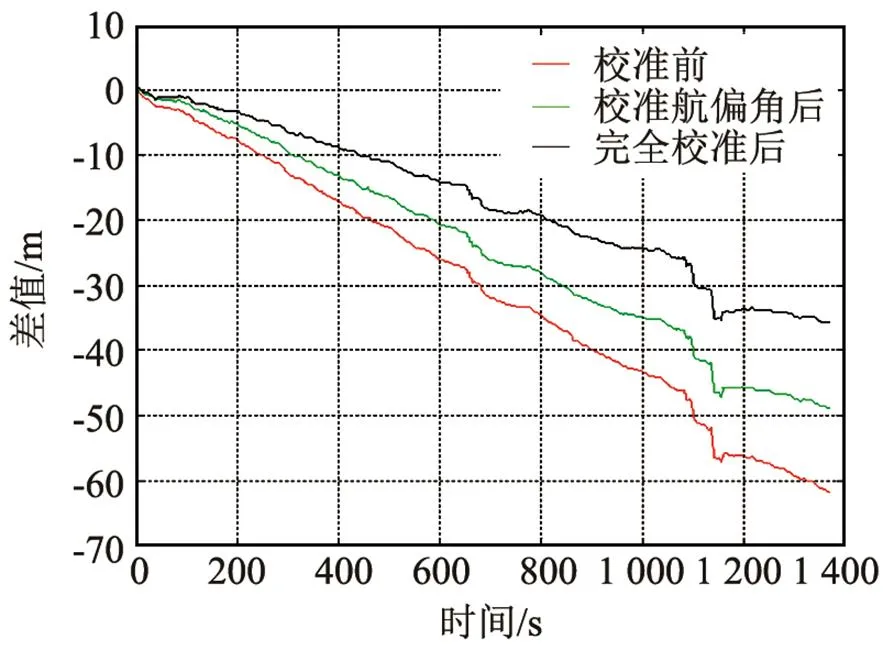
图10 直线航行的横向位移误差

图11 直线航行的纵向位移误差

图12 直线航行垂向位移误差

图13 弧线航行横向位移误差

图14 弧线航行纵向位移误差

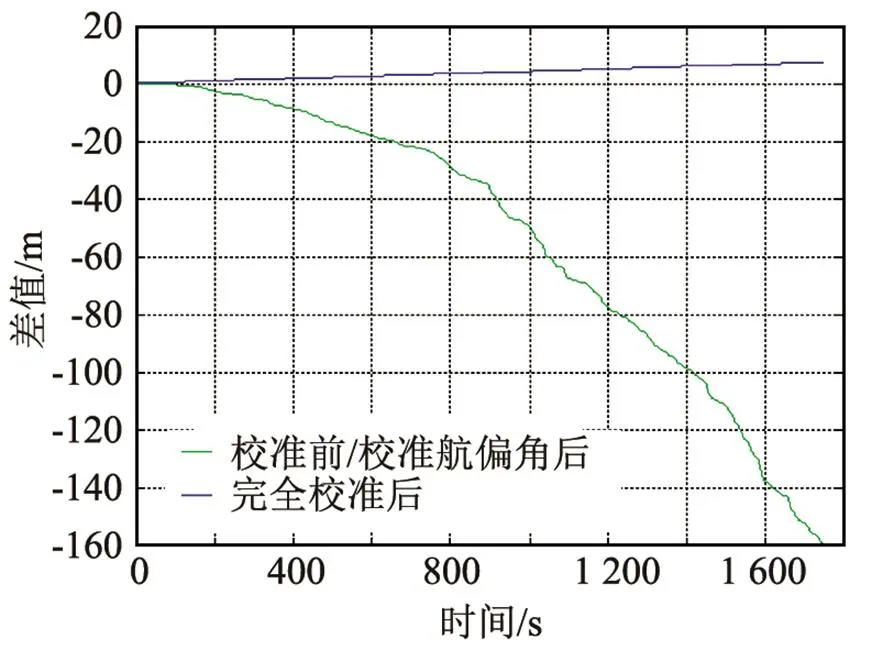
图15 弧线航行垂向位移误差

(2) 直线航行时误差增加比较稳定，弧线航行时，安装偏角造成的误差变化丰富，对测量速度影响较大。

(3) 安装航偏角对二维平面上误差的影响最大，横摇角和纵摇角在三维空间上看，对垂向位移误差影响最大，随着载体不断前行，偏离实际航线的距离累积变大，而经过校准的多普勒测速仪能够明显改善测速仪得到的速度精度，校准后得到的航行轨迹明显更贴近于实际航迹。

表1和表2展示了航偏角、纵摇和横摇偏角在校准前后对误差的影响情况。表1采用标准差形式将校准前后的值与GPS航迹比对，表2采用测线终点位置结果进行比对。

对比两种航迹，可以看出直线航行时的校准效果优于弧线航行，主要误差来源是多普勒测速仪获得的斜距误差，这是因为实际试验的湖底往往是不平整的，并且水深采用了试验区域的一个均值，但是仍然较好地实现了多普勒测速仪的校准，效果优于原始数据。结果比对可以看出，航偏角仍然是校准误差的主要来源，因此如果想优化校准效果，仍然需要从航偏角入手减小校准误差，这里采用了对底测速，校准结果依赖于GPS的精度，倘若可以采用对水测速，笔者认为无论从最终效果还是实际水面上的试验结果，都将优于对底测速校准，下一步工作将着重于多普勒测速仪对水测速的航偏角校准。

表1 校准前后两种航行标准位移误差的对比

表2 校准前后两种航行测线终点位置的对比

3 结论

本文采用了速度比值法来校准航偏角，在航偏角的估值基础上计算纵摇和横摇的角度，方法实现简便、运算量小。从试验结果来看，该方法很好地改善了三维安装偏角的安装误差，提高了测速仪的测速准确度，外场试验验证了该方法的有效性。

[1] 曹忠义, 郑翠娥, 张殿伦. 声学多普勒速度仪安装误差校准方法[J]. 哈尔滨工程大学学报, 2013, 4(34): 434-439.

CAO Zhongyi, ZHENG Cui’e, ZHANG Dianlun. A study on the calibration of installation error in acoustic transducer[J]. Journal of Harbin Engineering University, 2013, 4(34): 434-439.

[2] DOISY Y. Theoretical accuracy of doppler navigation sonars and acoustic doppler current profilers[J]. IEEE, 2004, 29(2): 430-441.

[3] POLLARD R, READ J. A method for calibration shipmounted acoustic Doppler profiler and the limitation of gyro compasses[J]. Journal of Atmospheric and Oceanic Technology, 1989, 6(6): 859-865.

[4] TERRENCE M. On in situ calibration of shipboard ADCPs[J]. Atmospheric and Oceanic Technology, 1989, 29(2): 169-172.

[5] TRUMP C L. Calculation of ADCP alignment offsets using single-beam velocity and depth data[J]. Journal of Atmospheric and Oceanic Technology, 1997, 14(5): 1252-1255.

[6] 胡华烜, 朱敏. 大倾角时的声学多普勒测速公式误差分析[J]. 海洋技术, 2008, 27(3): 39-42.

HU Huaxuan, ZHU Min. Error analysis of acoustic doppler velocity measurement formula at high angle[J]. Oceanography, 2008, 27(3): 39-42.

[7] TRUMP C L, 1986: Estimating absolute current velocities by merging shipboard Doppler current profiler data with LORAN-C data[C]//Proc. IEEE Third Working Conf. on Current Measurement, 177-183.

[8] 刘德铸, 郑翠娥, 张殿伦. 传感器安装误差在声学多普勒计程仪中的校准[J]. 传感器与微系统, 2009, 28(11): 71-73.

LIU Dezhu, ZHENG Cui’e, Zhang Dianlun. Calibration of sensor installation error in acoustic Doppler log[J]. Sensors and Microsystems, 2009, 28(11): 71-73.

[9] ROWE, F D, YOUNG J W. 1979: An ocean current profiler using Doppler sonar[C]//IEEE Proceedings Oceans, 1979, 292-297.

[10] 袁书明, 曹忠义. 基于航迹-航深信息的声学测速基阵校准技术研究[J]. 声学技术, 2017, 36(5): 431-436.

YUAN Shuming, CAO Zhongyi. Research on acoustic velocity array calibration technology based on track and navigation depth information[J]. Technical Acoustics, 2017, 36(5): 431-436.

Study on the calibration method of acoustic Doppler velocimeter

QIAO Zi-hang1,2, ZHU An-jue2, YANG Rui1,2

(1. Shanghai Acoustic Laboratory, Institute of Acoustics, Chinese Academy of Sciences, Shanghai 201815, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)

In order to improve the accuracy of acoustic Doppler velocimeter, the deviation angles between the velocity transducer and the carrier in the process of installation can not be ignored. The deviation angles include yaw angle, roll angle and pitch angle. A calibration method in three dimensional space is proposed in this paper. By using high-precision GPS navigator and Doppler velocimeter to measure bottom velocity, the yaw angle can be calibrated in terms of the velocity ratio. Then, by the geometric relationship of longitudinal profile, the magnitudes of pitch angle and roll angle are obtained from the yaw angle. Thus, the calibration of the 3D directional Doppler velocimeter is completed and the Doppler velocimetry coordinates and the carrier vector coordinates can be transformed accurately, which makes the accuracy of acoustic Doppler velocimeter improved. The effectiveness of this method is proved in field tests. The analysis results show that the main error of velocity measurement in two dimensional plane is caused by yaw angle, however, in three dimensional space, particularly for measuring vertical velocity, the error is mainly caused by roll angle and pitch angle.

acoustic Doppler velocimeter; calibration error calibration; three dimensional calibration;Speed ratio method

TB565+.2

A

1000-3630(2019)-03-0284-06

10.16300/j.cnki.1000-3630.2019.03.008

2018-04-26;

2018-06-28

国家自然科学基金资助项目(11574249、11074202)

乔梓航(1993－), 男, 山东烟台人, 硕士, 研究方向为声学多普勒测速仪校准技术。

朱安珏, E-mail: 13918199486@163.com