平面内三向轴压作用下新型毂形节点有限元分析

石城林

（中铁第四勘察设计院集团有限公司 湖北武汉 430063）

1 引言

节点是单层网壳结构的重要组成部分，节点的强度、刚度直接影响到单层网壳的受力性能。节点的破坏将引发与之相连件的破坏，进而致使结构失效。因此，合理的节点形式对单层网壳结构是至关重要的。当前我国网壳结构中最常用的节点形式有螺栓球节点和焊接空心球节点。这两种节点的研究已相对成熟，规范中亦给出相应的承载力计算公式。然而这两种节点运用在圆管截面中较多，矩形钢管节点的研究则相对较少。董石麟，郉丽［1-2］等对矩形钢管焊接空心球节点进行了试验研究和有限元分析，并根据薄壳理论提出了轴力、弯矩作用下矩形钢管焊接空心球承载力的实用计算方法；陈敏［3］等根据“杆件仅上下翼缘板及两根内力最大杆件的腹板与节点核心区焊接”的思路，提出了核心区采用两块端板和实心柱体两种构造形式的节点，通过10个典型节点足尺试验研究及有限元分析，验证了该节点的可靠性；王先铁［4］等提出一种新型毂形节点，通过与焊接空心球节点的对比试验，得出在节点直径及壁厚相同的条件下，新型毂形节点的极限承载能力比焊接空心球节点的极限承载力高，并提出了一定尺寸范围内的节点单向轴压极限承载力公式。

新型毂形节点具有良好的受力性能，但文献［4］中只对该节点在单一方向受力进行了研究，而在实际的网壳结构中，节点往往是受多向轴力的作用。本文根据网壳结构中节点常受到近似于平面内三向轴力作用的特点，运用大型有限元软件ABAQUS，理想弹塑性应力-应变关系和Von-Mises屈服准则，同时考虑几何非线性，建立了新型毂形节点有限元模型，对新型毂形节点在单向轴力和平面内三向轴力作用下进行对比分析。

2 有限元分析验证

文献［4］对新型毂形节点进行了试验研究。为保证本文有限元分析的准确性，首先对文献［4］中第一组试件进行了有限元模拟验证。根据文献［4］中的数据，毂形节点直径为350 mm，壁厚为20 mm；采用Q235B钢材，屈服强度为287.4 MPa，极限强度为312.5 MPa，伸长率为22.39%。与节点相连的杆件截面为□150×150×16×16，杆件长425 mm；采用Q34B钢，屈服强度为385.46 MPa，极限强度为496.87 MPa，伸长率为25.49%。根据文献［4］中试验结果，3组新型毂形节点单向轴压极限承载力平均值为3 950 kN。

节点的有限元模拟分析采用大型有限元软件ABAQUS进行，几何模型根据文献［4］中的试件数据建立。有限元模型采用四节点减缩积分格式的壳单元S4R，为满足精度要求，在壳单元厚度方向，采用9个积分点的Simpson积分。S4R单元允许沿厚度方向的剪切变形，随着壳厚度的变化，求解方法会自动服从厚壳理论或薄壳理论，当壳厚度很小时，剪切变形很小，并且考虑有限薄膜应变和大转动，适合大应变的分析。钢材根据试验数据，采用双折线随动强化模型。

采用ABAQUS有限元模拟，得到文献［4］中第一组新型毂形节点单向轴压极限承载力为4 215 kN，与试验结果相差约6.7%。考虑试验中试件加工时试验两端杆件可能存在偏心，以及试件加工时焊接残余应力的影响，有限元结果相比试验结果偏高是合理的。

根据有限元分析结果可知，随着荷载增大，节点端板及杆件端板逐渐发生塑性变形，节点端板尤为显著。最终节点达到极限承载力时，节点端板产生明显屈曲。破坏形态与文献［4］中试验破坏形态描述一致。

因此，本文采用有限元分析能够较好地模拟新型毂形节点受力状态。

3 三向轴压有限元模型

在大多数网壳中，与同一节点相连的杆件近似在一个平面内，而在这个平面内则成较相近的角度［5］。经有限元试算，当杆件在平面外有较小的夹角时，节点的极限承载力与杆件没有平面外角度时非常接近。因此，为便于分析，本文建立的模型杆件均在同一平面内，且相邻杆件间的夹角为60°。同时，建立截面尺寸、壁厚相同而仅有单一方向杆件的节点进行对比分析。模型如图1所示。

由于不同的钢材强化程度有所不同，在后续计算中假定钢材为理想弹塑性材料，取弹性模量为2.06×105N／mm2、屈服强度为 235 N／mm2、泊松比为0.3，屈服准则为Von Mises屈服准则。

虽然节点为平面内三向受力，但ABAQUS中模型为三维空间模型，故对杆端在Z向位移也加以约束。约束其中3根杆件的三个方向的线位移，对余下的3根杆件采用主动加载，并约束垂直于杆件方向的线位移。经试算，当对两侧杆施加小于中杆的力时，节点极限承载力介于单轴受压与平面三向等轴力受压之间。为减少不确定变量，本文仅研究平面三向等轴力的情况。边界条件如图2所示。

图1 试件简图（单位：mm）

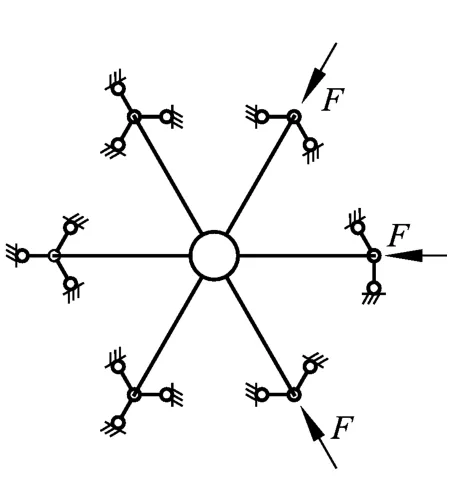
图2 边界条件

4 应力应变分析

当节点板板厚与杆件截面相差不多时，破坏形态表现为节点区破坏。以杆件壁厚为16 mm、节点壁厚为20 mm的节点为例进行说明。在平面三向轴力的作用下，当荷载较小时节点的应力分布较为均匀，塑性区最早出现在杆件夹角处应力集中的部位。随着荷载的增大，杆件近节点区一端也出现塑性区。荷载不断增大，塑性区不断扩展，节点端板逐渐出现平面外变形，最终节点发生破坏。节点破坏时，节点端板及杆件近节点区一段发生明显屈曲。破坏模式与单向轴压作用下类似，均为节点端板屈曲破坏。节点破坏时的等效塑性应变分布如图 3所示［6-8］。

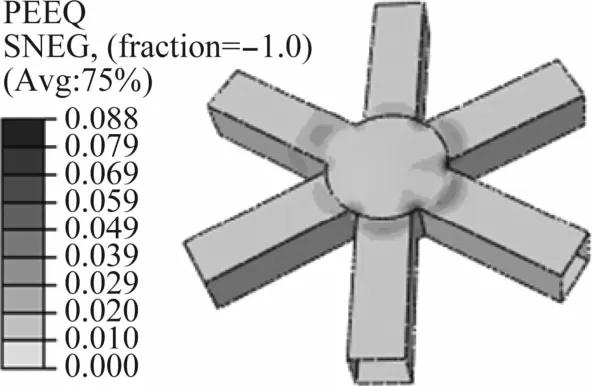
图3 节点等效塑性应变分布

当节点板板厚远大于杆件截面时，试件破坏时节点端板不再发生屈曲，破坏形态表现为杆端破坏［9-10］。

5 两种荷载模式作用下的对比

在单向轴力和平面内三向轴力两种情况下，新型毂形节点的破坏形态基本相同，破坏时节点端板均发生明显屈曲变形。不同的是当节点破坏时，单向轴力作用下节点径向变形较大，由圆形压成椭圆形；而在平面三向轴力情况下，作用在平面各方向上的力大小均匀，毂环在环向被约束，使得节点区沿径向变形较小。在三向轴力作用下节点的极限承载力比单向轴力作用下略小。究其原因，主要是由于节点端板在三向轴力作用下受到的压应力更大，节点端板更容易发生平面外屈曲破坏。经过大量试算，三向轴力作用下节点的极限承载力约为单向轴力作用下的0.85～0.95倍，该比值与杆件、节点区横截面尺寸及壁厚有关。

6 节点区壁厚对承载力的影响

当节点区壁厚越大，节点端板平面外刚度越大，节点端板的屈曲越不明显。随着节点区壁厚的增大，节点的破坏模式由节点端板屈曲破坏逐渐向杆件屈服模式过渡。

图4绘出了杆件壁厚为16 mm的不同节点区壁厚荷载位移曲线。从图4可以看出，随着节点区壁厚的增大，节点的刚度不断增大，节点的极限承载力逐渐提高。但当节点区壁厚与杆件壁厚之比大于1.5时，节点极限承载力几乎不再随节点区壁厚而提高，这时试件的破坏模式已为杆件屈曲破坏。同时，从图4也可以看出新型毂形节点具有较好的延性［11］。

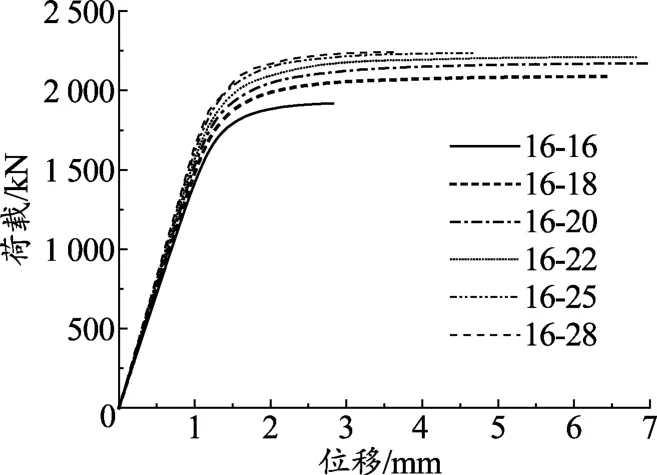
图4 不同节点区壁厚荷载-位移曲线对比

7 提高节点抗压承载力的建议措施

从前文分析可以得出，节点的破坏主要形态为节点端板屈曲破坏。从图4可以看出，增大节点板厚度，提高节点端板的抗屈曲能力可以有效提高节点的极限承载力。但当节点直径较大时，节点端板平面尺寸较大，靠加大节点板厚度提高节点承载力显然不经济，而且会使节点自重增加，增大结构负担。当节点端板平面尺寸较大时，可在节点区设置十字肋板，加强对节点端板的约束，延缓节点端板发生屈曲，提供节点的极限承载力［12］。

8 结束语

在合理选择单元类型、材料本构的基础上，建立了新型毂形节点有限元模型。考虑了几何非线性的影响，对新型毂形节点在平面三向等轴力作用下进行全过程受力分析，并与单轴受力的荷载模式下进行对比。主要得到以下结论:

（1）有限元分析能够较好模拟新型毂形节点的受力状态。

（2）新型毂形节点在单向轴力、平面内三向轴力作用下受力性能良好。

（3）在平面三向等轴力作用下节点的极限承载力比单向轴力作用下极限承载力小约5%～15%。

（4）当节点区壁厚与杆件壁厚之比小于1.5时，加大节点区壁厚可以显著提高节点极限承载力；当节点区壁厚与杆件壁厚之比大于1.5时，加大节点区壁厚对提高节点极限承载力作用不大。

（5）当节点区平面尺寸较大时，可在毂内加肋以减缓节点端板的屈曲，进而提高节点的极限承载力。