煤矿突发事件应急救援能力评价与定位研究

陈方旻，潘 兵

(淮南师范学院 经济与管理学院，安徽 淮南 232001)

煤矿安全事故频发一直制约着我国煤矿行业发展，困扰相关企业和政府部门。近年来，煤矿企业通过提升安全生产技术、强化安全风险意识、加强应急救援水平等措施，预防和治理安全突发事件，但整体水平与部分发达国家仍存在较大距离[1]。据全国安全工作会议公布数据显示，2016年我国共发生煤矿安全事故249起，死亡人数538人，5省份全年发生安全突发事故超过15起；2017年，我国煤矿共发生事故219起、死亡375人；2018年共发生事故224起、死亡333人，煤矿百万吨死亡率0.093[2]。先前研究表明，事前监测预备、事中应急处置、事后恢复总结，有利于降低煤矿突发事件的发生频率和损失程度[3]。由于煤矿应急救援水平对煤矿突发事件的发生概率，以及突发事件带来的损失有显著影响，因此，客观地构建应急救援能力评价体系，并精准化对其进行定位，是学术界和实践界一直追求破解的难题。

近年来，学者们分别从不同视角对煤矿应急救援能力展开研究。姜伟运用模糊综合评价方法对矿井火灾救援能力进行研究[4]。冯珍采用专家打分法计算煤矿突发事件应急救援评价体系指标的权值[5]。杨力运用熵权法对煤矿应急救援能力进行研究[6]。李新春运用ExtendSim仿真软件对煤矿突发事件应急救援展开分析，构建应急救援仿真模型[7]。汪刘凯运用因子分析、结构方程对煤矿安全救援影响因素展开分析，确定各关键要素间作用路径[8]。温廷新运用三角模糊数对煤矿应急处置流程展开分析，构建煤矿突发事件随机Petri网络[9]。

上述文献表明：关于煤矿突发事故应急救援能力的研究，主要采用专家打分法、调查访问、综合评价、因子分析、结构方程模型等方法，而煤矿突发事故应急救援能力影响因素众多，评价指标数据的模糊性、不确定性极高。因此，先前采用的评价方法虽然在一定程度上有利于降低煤矿突发事件的损失程度，但是其在评价指标权重上受主观性影响相对较强，评价结果的精准性、可视性、易理解性有待进一步提升。而信息熵(Information Entropy)根据提供信息的多寡有效刻画评价指标的重要度，可以有效分析、判断、处理各种不确定、不精确、不完备信息，降低对先验知识依赖程度和评价过程的主观性，因而有利于提升煤矿突发事件救援能力评价的客观性和精准性[10]。并且，本文创新性将服务管理中IPA定位方法(Importance-Performance Analysis)引入煤矿突发事件应急救援能力评价中，对每一评价指标的“重要性-表现性”得分进行定位，将评价结果可视化、清晰化展示，从而提升评价结果的易理解性。因此，本文运用信息熵确定煤矿突发事件应急救援能力评价指标的权值，采用IPA对评价对象重要度及其表现值进行定位分析，并选取相关煤矿展开实证性研究，从而证实该方法对煤矿突发事件应急救援评价的有效性。

一、理论基础

(一)信息熵理论

“熵”来源于热力学，最早于1856年用来表示热力变化的容量，形容物质系统中能量衰竭程度[11]。随着“熵”的进一步发展，N.Wiener和C.E.shannon(1948年)将“熵”引入信息论和通信科学中，并提出了信息熵的概念[12]。在信息科学与决策科学中，信息熵用来反映表示指标变异程度，指标熵值越小，权重越大，其提供的信息量就越大；反之，指标熵值越大，权重越小，其提供的信息量就越小。近年来，由于信息熵可以用来描述不确定性选择和随机事件等，有效解决了信息识别难题，因此在信息领域、光学领域、物理学领域、生物学领域以及管理科学领域获得了广泛应用[13]。根据信息熵的基本理论，本文将信息熵的计算步骤划分如下：

1)假设存在m个评价对象的n个指标，构建判断矩阵P

(1)

2)将数据标准化(离差标准化)

(2)

其中maxPij、minPij为第J个评价指标中最大值与最小值。

3)计算评价指标的熵值H

(3)

4)确定第i指标的熵权M

(4)

5)计算第j评价对象的综合得分zij

(5)

(二)IPA定位分析

二、信息熵-IPA评价与定位流程

根据信息熵理论和IPA定位法的优点，本文构建基于信息熵-IPA的煤矿突发事件应急救援能力评价与定位模型。将信息熵计算的各评价指标权重作为IPA分析的横坐标(重要性)，将信息熵计算的各评价指标的得分作为IPA分析的纵坐标(表现性)，具体计算流程见图1。

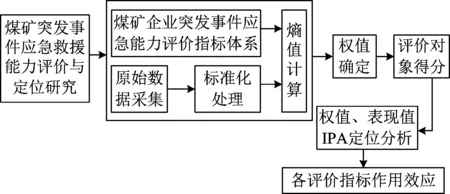
图1 煤矿突发事件应急能力评价与定位流程

三、实证研究

(一)实证对象简介及指标体系构建

本文选取义马煤业集团下属8家煤矿为实证对象，河南义马煤业集团股份有限公司位于在豫、晋、陕三省交界处，资源丰富，交通便利，经营范围主要涉及产焦煤、洗精煤、发电、造气、炼焦等多领域，公司整体实力位于中国500强中列[16]。本文依据本人前期关于煤矿突发事件安全管理的相关研究结果，参考《义马煤业预防安全事故规定》《义马煤业应急救援指导意见》等相关材料，最终构建事前检测、事中处置、事后恢复三维度的煤矿突发事件应急救援能力评价体系，具体评价指标见表1[6-9]，①。

(二)数据收集与清洗

本文采用河南省煤矿安全监察局2016年煤矿安全标准化考核结果作为原始数据。在数据清洗中，对于少量缺失数据运用均值填充进行修补。最终收集义马煤业突发事件应急救援能力的原始数据如表2所示。

表1 煤矿突发事件应急能力评价指标体系

表2 煤矿突发事件应急能力评价初始数据

(三)指标权值确定

为使该评价分析模型科学、简洁、可拓展，根据计算公式(1)—(5)运算原理，本文运用R语言对上述评价模型进行编程计算，执行相关代码，各评价指标权值(保留4位小数)运算结果如表3所示。

表3 煤矿突发事件应急能力评价指标权值

执行代码“summary(x$w)”，对上述评价指标进行简要分析，结果如表4所示。

表4 煤矿突发事件应急能力评价指标权值分析表

表4显示，对32个指标权值展开简要分析中，最小值为0.0200，最大值为0.0541，中位数为0.0292，均值为0.0313，第一四分位数为0.0247，第三四分位数为0.0347。

分别执行“> x$value”、“> x$order”，计算出各评价对象具体得分与排名，具体结果如表5所示。

表5 煤矿突发事件应急能力最终得分与排序

表5显示，在总体应急能力得分中n5分值最高为84分，n4、n8分值最低为70分，在总体应急能力排序中n5位列第一，n2、n3、n7并列第二，n1位于第六，n4、n8并列第七。

(四)指标IPA定位分析

根据熵权法对煤矿应急救援能力指标的权重计算结果和评价指标具体表现值，运用服务管理中IPA定位分析法，分别以重要性为纵坐标，表线性为横坐标，以均值(i,p)=(0.0313,74.89)构成交点坐标，对煤矿应急能力评价指标展开IPA定位分析，见图2。

图2 煤矿突发事件应急救援能力定位分析

根据图2对8所煤矿的应急救援能力评价指标IPA分析结果，得到8所煤矿应急救援能力评价指标作用区域，将其具体分析，结果如表6所示。

表6 煤矿突发事件应急救援能力评价指标定位区域

注：上表区域划分中，当i=0.0313时当作i<0.0313处理

四、结论与建议

本文运用信息熵、IPA定位分析等理论与方法，构建基于信息熵-IPA的煤矿突发事件应急救援能力评价与定位模型，识别不同评价指标在整体救援中的重要程度，判定不同煤矿应急救援能力水平，甄别不同指标在不同煤矿救援中作用效能，发现煤矿突发事件应急救援能力整体特征。主要结论、建议有：

1)根据熵权计算结果，煤矿突发事件应急救援能力影响因素中，消防抢险(m15)重要度最强为0.0567，其次是应急培训(m8)为0.0532，应急预案修订(m28)重要度最低为0.0194；因此，在煤矿安全管理实际工作中，可以参考上述各因素中权值，加强重要因素(如：技术支持、消防抢险等)的内涵建设，从而在应急救援中充分发挥效能。

2)根据义马煤业集团下属的8家煤矿评价结果，煤矿n5得分最高为84分，在整体排名中位于第一，在实际中n5煤矿连续多年来被评为“安全示范单位”，煤矿n4、n8得分最低为70，排名最后；因此，该评价结果有效证实了模型的科学性、客观性，在实际煤矿安全管理中，可考虑煤矿n4、n8学习n5的应急管理方法。

3)根据IPA定位分析结果发现，不同煤矿在改进区、观察区、维持区、优势区都分布不同影响因素，其整体应急水平取决于各评价因素间相互作用；因此，在煤矿实际应急管理中，应根据自身实际定位分析情况，优先加强改进区因素，密切监测观察区因素，扎实稳固维持区因素，持续稳定优势区因素。

4)根据IPA区域划分结果，不同煤矿在各区域分布因素数量各异(如：n5在优势区分布多改进区分布少，n8在改进区分布多优势区分布少)，安全评价得分越高优势区分布因素越多(如n5、n3)，安全评价得分越低该进区分布因素越多(如n4、n8)；在煤矿实际应急能力管理中，应急水平低的煤矿往往面临基础差、整改任务多双重压力，集团公司应该重点关注整体水平低的煤矿，多方面帮助低水平煤矿提升应急救援能力。

注释：

① 义马煤业集团公司安全管理规章制度[Z].义马煤业集团出版社，2016.