让儿童在问题情境中建构概念——以“倍的认识”为例

◇马 宇

【课前思考】

一 教学现状

提起“倍的认识”，很多教师的头脑中会出现如图1这样的图像：

图1

也会出现这样的句式： 把2 朵红花看作一份，黄花里有3 个2 朵，我们就说黄花的朵数是红花的3 倍。由此可见，在“倍”概念的学习中，教师过于关注概念表述的“精确”，而忽略了其实质和实际的背景。

二 理清概念网络

“倍”的产生源于比较，在小学阶段，如果以“倍”概念的构建作为一个观察点，往前看，我们可以看到一、二年级的“比多少”，因为“倍”和“比多少”的共同点都是说明两个量之间的关系，不同的是“比多少”重点关注多出的部分——儿童可以利用已知经验数出来，而“倍”关注的是多倍量整体——儿童需要先圈，再数出圈的个数；往后看，我们可以看到“分数”“比”，因为在生活中或儿童继续学习数学中，会发现两个数量的倍数关系不仅有整数还有分数；不仅同类量有倍数关系，非同类量也有倍数关系——比如, 速度＝距离÷时间。

三 借问题情境形成概念体系

由于建构“倍”概念，需要儿童实现从绝对数量的比较到相对数量比较的飞跃，具有一定的抽象性和概括性，而儿童的思维具有具体、形象的特点，为了解决这一矛盾，需要教师精心设计典型性、启发性和趣味性兼备的问题情境，以促使儿童经历一个主动建构、层层递进、内化深入的思维过程，在头脑中逐步形成关于“倍”的概念系统。

一 问题情境向前面延伸： 激活经验——让

【课堂实践】儿童获得概念意象

在课始，我们把学校的烘焙课程搬到了数学课堂，通过比较香甜的蛋糕和比萨的数量，既营造了温馨的学习环境，同时促进儿童主动将一年级学习过的“比多少”和本节课要学习的新概念“倍” 进行关联，并在此基础上让儿童初步理解“倍”。

【片段一】生成“倍”的认识

师：看，老师给大家带来了什么？

生：蛋糕。

师：还准备了一些比萨，比萨的块数比蛋糕多一些，可能是几块呢？

（根据学生的回答，课件出示图2）

图2

师：在这三幅图中，哪一幅中比萨多出的数量最与众不同?你是怎么想的？

生1：第二种，因为比萨比蛋糕多出来的是双数，其他多出来的是单数。

生2：第一种，因为多出来的比萨最少。

生3：第三种不同，因为比萨多出来的和蛋糕一样多。

（大多数同学都表示同意生3 的意见）

师：既然多数同学都觉得第三幅最特别，就请你用自己喜欢的方式来表达6 和3 之间这种特殊的关系吧。

（学生独立练习，然后展示） 层次一：3+3=6，6=3+3，6-3=3； 层次二： 二三得六，2 个3 是6，6 里面有2 个3；层次三：6 是3 的2 倍。

教师抓住层次三追问：2 在哪里？［指名学生到黑板上圈一圈（如图3）］

图3

师：谁有问题要问他？

生1：为什么要3 个圈在一起？

生2：因为蛋糕就是3 块。

师：你们知道他把几块看作1 份了吗？

生：把3 块看作1 份。

师：明明是3 块蛋糕，为什么要说成是1？

生2： 因为比萨都是和蛋糕比，所以要把3块蛋糕看作1 份。

师：把3 块蛋糕看作1 份，比萨就有这样的2 份，我们就说比萨的块数是蛋糕的2 倍。

师：通过刚才研究比萨和蛋糕“比多少”的情况，我们知道了其中还会出现1 份和几份的关系，这就是我们今天要认识的新朋友“倍”（板书课题）。

【片段二】巩固“倍”的认识

课件出示图4。

图4

师：比萨挺调皮的，看，现在比萨的块数是蛋糕的几倍？

生：2 倍，因为虽然比萨放乱了，但蛋糕还是3 块，比萨也应该把3 块当1 份，有这样的2 份。

师：“几倍” 说的是两个数量之间的关系，与位置无关。

二 问题情境往宽处打开：多元表征——让儿童掌握概念本质

布鲁纳认为，在人类的智慧生长期，有3 种表征系统在起作用，即动作表征、表象表征和符号表征。因此，帮助儿童掌握“倍”概念的本质，不仅是引导他们说出具体情境中两个量的倍数关系，而且需要设计一系列的变式，需要儿童通过观察、发现、归纳，灵活运用多种形式去表征，诸如摆学具、画图示、说关系、列算式等，才能建构起对“倍”的深刻认识。

【片段三】提升“倍”的认识

小组合作：画图表示比萨的块数是蛋糕的3 倍。

师： 大家能想象出这幅图是什么样的吗？小组同学先商量一下，再把想法表示出来。

1.小组活动，教师巡视。

2.交流展示。

组1：我们有两种方法，一种是把蛋糕去掉1块，这样6 里面有3 个2，比萨是蛋糕的3 倍；另外一种是蛋糕不动，再添上3 块比萨，比萨也是蛋糕的3 倍。（图略）

组2：我们的方法是这样的。（如图5）

图5

组3：他们组画的太麻烦了，我们可以画一个图表示。（如图6）

图6

组4：我们同意第三组的想法，不管蛋糕有几块，只要比萨有3 份蛋糕那么多，比萨的块数就是蛋糕的3 倍。

师：你们真了不起！请认真观察这几幅图，它们有什么相同点？

师：一般情况下，我们往往以较小的数为标准，把它看作1 份，较大的数正好有这样的几份，我们就说较大的数是较小的数的几倍。

【片段四】深化“倍”的认识

师：现在我们把神奇的圈圈请上大屏幕（如图7），红色部分是绿色部分的几倍？

图7

师：观察图8，绿带子的长是红带子的几倍？

图8

生：绿带子的长是红带子的5 倍，因为形状虽然变了，但还是把绿带子看作1 份，红带子有这样的5 份。

师：观察图9，现在绿带子的长是红带子的几倍？

图9

生：还是5 倍，虽然红带子换了位置，但还是把它看作1 份，绿带子有5 份那么长。

师：观察图10 的变化，让带子细一些、再细一些，你们有什么发现？

图10

生：带子越来越细，最后变成了线段。

师：在这条线段上，你能找到哪些倍数关系？

生1：5 倍，把前面的一小段看作1 份，后面的线段就有5 份，后面线段的长是前面线段的5 倍。

生2：6 倍，我也把前面的一小段看作1 份，整条线段的长就有这样的6 份，所以整条线段的长是前面线段的6 倍。

生3：3 倍。

学生上台介绍，教师出示课件，如图11。

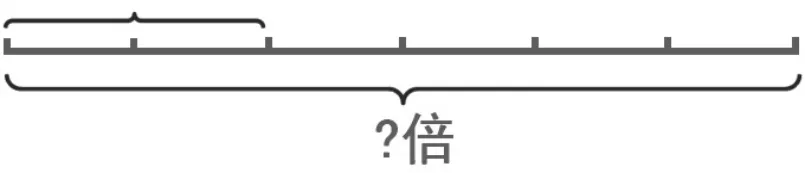
图11

师：如果给大家足够多的时间，相信你们能找到更多的倍数关系。（如图12）

图12

师：请看最后一条线段，后面线段的长是前面线段的几倍？你是怎么想的？

生：1 倍，因为前面和后面线段的长都是3份，所以可以说后面线段的长是前面线段的1倍，也可以说前面线段的长是后面线段的1 倍。

师：同学们分析得真好！在讲几倍时，我们经常以较小数为标准，但当标准由较小数变成较大数时，我们又该怎样来表达它们之间的关系呢？这个问题有挑战性，让我们再回到甜蜜的烘焙乐园。

三 问题情境朝后面整合：深度思维——让儿童形成概念体系

孤立的数学概念是不存在的，为了营造儿童生成概念体系的外部环境，我们就要立足于数学知识的逻辑结构，让儿童看清知识本质、理顺知识关系。由于“倍”隶属于“两数之间的关系比较”，与“比”一起架构起两数“倍比关系”的表示方式，因此本节课中儿童对“倍”的认识,不能仅仅停留在“几份”或“几个几”上面，还要让学生感悟到“倍”与“比”之间的关系，即通过“凸显‘标准’学习‘倍’”“变换‘标准’引‘分数’”的学习途径，让儿童通过深度思维沟通“倍”“比”的联系，逐步形成有关“比率”的概念系统。

【片段五】完善“倍”的认识

1.逆向思考，沟通倍与分数。

师：刚才我们以蛋糕为标准，说比萨的块数是蛋糕的2 倍。 如果现在以数量多的比萨为标准，蛋糕的块数是比萨的几倍呢？（课件出示图13）

图13

生1：2 倍。

生2：1 倍。

生3：1 倍也不到。

师：如果以比萨的块数为标准，蛋糕的块数正好是它的一半，我们就说蛋糕的块数是比萨的半倍，半倍在数学上可以用一个数“”来表示，这是一个分数，读作：二分之一。

师：还是以比萨为标准，去掉1 块蛋糕，蛋糕的块数是比萨的几分之一？

2.延续情境，初步认识“比”。

师：大家知道吗，到了六年级，我们刚刚分析的蛋糕和比萨的数量关系还可以写成1∶2，读作：一比二。这个比又表示什么意思呢？和“倍”有什么关系呢？我们以后再学习。