S掺杂调节SnTiO3带隙的第一性原理研究

魏丽静，郭建新

(1.华北电力大学科技学院，保定 071051；2.河北大学物理科学与技术学院，保定 071002)

1 引 言

随着社会的不断进步，人们对能源的需求日益增多，但传统的化石能源具有高污染和不可再生性，探索清洁能源成为科研工作者的一个重要课题。太阳能是众多的可选清洁能源中最具发展潜力的能源之一[1]。众所周知，可见光占太阳总辐射的约50%，要想有效地利用太阳能，就要充分吸收可见光。根据光电效应原理，只有光子的能量大于半导体的带隙宽度，光子才能激发材料价带的电子跨过禁带到达导带，从而在材料内部产生电子-空穴对。因此，为了能够高效的进行光吸收和能量转换，光伏材料的带隙范围要在1.1～2 eV之间，最佳的带隙宽度在1.4 eV左右。另外，为了使产生的电子-空穴对向相反方向移动来产生光电流，最典型的做法就是引入p-n结，产生内建电场来分离电子-空穴对，阻止它们发生复合。目前，应用最广泛的晶硅太阳能电池就是基于p-n结原理而工作的，但令人遗憾的是Shockley-Queisser(SQ)效率极限理论提出，这种基于p-n结光伏效应的太阳能电池的转换效率理论上不会高于33.7%[2]，这使得这类太阳能电池的发展和应用受到了极大的限制。

最近，铁电材料的反常光伏效应引起了人们的关注，它来源于铁电材料的自发极化状态[3-5]。自发极化的存在可以将存在于体材料中的电子-空穴对分离而产生光生电流，这是一种体材料的效应，因此称为体光伏效应。这种体光伏效应给我们提供了不同于传统p-n结太阳能电池的一种新的光电转换方式。但铁电光伏材料的致命弱点是极小的光生电流，这主要是由于绝大多数铁电材料的带隙都大于3 eV，对于可见光的吸收非常有限。因此，降低铁电材料的带隙宽度是发展铁电光伏材料的重要一步。BiFeO3是铁电材料中带隙较窄的材料之一，带隙为2.7 eV[6]，但相比于最佳带隙1.4 eV仍然很大。通过结构转变[7]和过渡金属原子掺杂[8-9]都可以有效的降低铁电光伏材料的能带带隙。例如，实验上利用Cr的掺杂可以将BiFeO3的带隙降低到1.43 eV[8]，转换效率达到8.1%，这给铁电光伏的发展带来了曙光。除了通过阳离子替换掺杂来降低带隙外，阴离子B，C，N，F，Cl，Br和I的掺杂也是一种可行的方法[10-11]。其中，S与O同族，二者具有相同的化合价态，S用来替换O不会造成原有体系的电荷平衡而产生缺陷。有研究人员使用第一性原理方法研究了S掺杂到PbTiO3中对带隙的影响，发现S的加入可以有效的降低PbTiO3的带隙(带隙降低约1.3 eV)，为PbTiO3应用于铁电光伏提供了一种途径[12]，但众所周知，PbTiO3是一种环境不友好的材料。Sn与Pb同族，具有与Pb类似的电子结构属性。SnTiO3也是一种新型的潜在的室温铁电材料，具有比PbTiO3窄的带隙宽度(2.6 eV)[13]。如果将S掺入到SnTiO3中，这必将对SnTiO3的带隙和极化强度产生影响。本文通过在SnTiO3中掺入不同含量的S，研究其晶体结构和能带结构的变化，探寻S对SnTiO3带隙调节的微观机制。

2 计算方法和理论模型

本文所有计算均采用第一性原理计算软件VASP程序包[14]完成。采用投影缀加波(PAW)方法来描述电子相互作用势[15]，广义梯度近似(GGA)的Perdew-Burke-Ernzerhof (PBE)来处理交换关联泛函[16]。计算模型采用平面波基矢来展开波函数，且平面波的截断能设置为500 eV，所有原子和晶胞弛豫的收敛精度为10-5eV，且原子受力设定小于0.2 eV/nm。众所周知，LDA方法会严重低估材料的带隙，因此本文中的带隙计算均采用更能接近实验值的杂化泛函HSE06[17]进行计算。SnTiO3为典型的四方钙钛矿结构(空间群为P4mm)[13](图1a)，有两种不同位置的O，计算得到S替换竖直方向O (Site1)的能量要低于平行方向的O (Site2) 0.72 eV，因此本文只对Site1位置的O进行替换。根据S的掺杂含量不同(图1b、c、d)，SnTiO3-xSx(x=0, 0.33, 0.5, 1)晶胞分别采用1×1×1单胞以及1×1×2和1×1×3的超胞结构，且分别使用12×12×12、12×12×6和12×12×4大小的Monkhorst-Pack[18]方案自动生成的k点网格进行计算。本文采用Bader电荷软件包[19]来分析SnTiO3和SnTiO2S的成键信息。

3 结果与讨论

3.1 S掺杂SnTiO3的体系结构

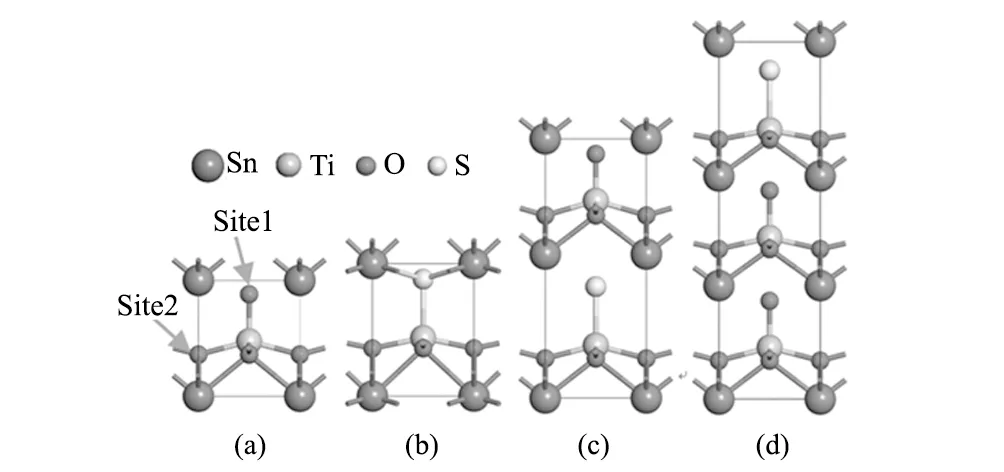
图1 不同S掺杂浓度的SnTiO3-xSx结构示意图 (a)x=0;(b)x=1;(c)x=0.5;(d)x=0.33。Site1和Site2为O的垂直和平行掺杂位置 Fig.1 Sketch map of SnTiO3-xSx with different S doping content (a)x=0;(b)x=1;(c)x=0.5;(d)x=0.33. Site1 and Site2 represent the vertical doping site and the parallel doping site of O atom, respectively

计算得到SnTiO3的晶格常数为a=0.380 nm，c/a的值为1.17，与之前的计算结果(a=0.385 nm，c/a=1.13)[20]相吻合。SnTiO3与PbTiO3相比[12]，具有更大的c/a值，有利于获得大的极化强度。如表1所示，当S掺入到SnTiO3后，SnTiO3-xSx(x=0, 0.33, 0.5, 1)仍然保持P4mm空间群，与SnTiO3一样具有四方结构。SnTiO3-xSx的晶格常数a与SnTiO3相比几乎不变，但晶格常数c发生明显的增大。当x=1时，c/a的值由SnTiO3的1.17增加到1.45(表1)。从图1可以看出，晶格常数c方向的变化主要来源于S所在八面体晶格的拉伸。例如，在x=0.5时，S所在八面体的c=0.541 nm，而没有S的Ti-O八面体的c=0.451 nm。可以看出，S掺入后主要改变S所在八面体的结构。c/a值的显著增大的现象在S掺杂PbTiO3上也被观察到[12]。在实验上，S替代O后能够引起金属氧化物的c/a值增大[21-22]，形成-S-M-O-M-S-的链状模式，这与我们的结果是一致的。S的掺入会引起SnTiO3原有阴阳离子的成键键长变化。由表2可以看出，Sn-ONV(图1a中Site1位置的O)键长和在c方向垂直距离随掺杂S的增加变化不明显，但要比没有掺杂时(即SnTiO3)减小0.007 nm。Sn-S的键长在x=0.33和0.5时保持不变，在x=1时键长减少0.003 nm，c方向垂直距离减少0.005 nm。Ti-ONP键长在x=0.33和0.5时几乎保持不变，垂直距离也相差较小，但x=1时，Ti-ONP的垂直距离变化相对比较明显，比SnTiO3时的Ti-ONP减少0.011 nm。Ti-ONV和Ti-S键长几乎保持不变。综上所述，当x=0.33和0.5时，只有Sn-ONV在c方向垂直距离要比未掺杂时有一些减少外，其它阴阳离子的键长变化都不是很明显，这说明当S掺杂量不大的时候对离子成键影响比较小。但当x=1时，Sn-S和Ti-ONP在c垂直距离都变化较明显，这说明较大的S掺杂对其离子成键有明显的影响，这也许是SnTiO2S具有金属性的原因。

表1 不同S掺杂浓度SnTiO3-xSx (x=0, 0.33, 0.5, 1)结构参数、能带和极化强度。c/a 比值为平均每个Ti-O/S八面体对应的数值Table 1 Calculated structure properties, bandgap and polarization of SnTiO3-xSx (x=0, 0.33, 0.5, 1). The c/a ratios are normalized according to the number of octahedral in the unit cell

表2 不同S掺杂浓度SnTiO3-xSx(x=0, 0.33, 0.5, 1)的键长及其垂直距离z的差值(NV表示最近邻垂直的位置，NP为最近邻平行的位置)Table 2 Bond lengths and z-displacements for SnTiO3-xSx (x=0, 0.33, 0.5, 1). NV and NP represent the nearest neighbor in vertical direction (along x or y axis) and the nearest neighbor in parallel direction(along z axis) to Ti position /nm

图2 能带图 (a)SnTiO3;(b)SnTiO2.5S0.5 Fig.2 Band structure (a)SnTiO3;(b)SnTiO2.5S0.5

3.2 S掺杂SnTiO3体系的电子结构特性

如表1所示，SnTiO3带隙的理论计算值为1.87 eV，比其它研究人员使用LDA方法的计算值0.967 eV[23]要大，这是因为LDA方法会低估能带计算值。但该计算值要比同样使用HSE方法的计算值2.175 eV[13]要小，这是因为作者使用的赝势与本文不同，而且该计算值基于Si基片上的SnTiO3薄膜晶格参数(a=0.384 nm，c/a=1.06)所得结果。由表1可知，当掺入S时，SnTiO3的带隙明显变小，达到1.01 eV，且掺入S的含量对带隙的影响不大，这种现象与PbTiO3掺S的结果是一致的[12]。值得注意的是，当S掺杂量达到x=1时，SnTiO2S为金属性，失去半导体性质。如图2所示，纯的SnTiO3和SnTiO2.5S0.5都是间接带隙。相比SnTiO3， SnTiO2.5S0.5的导带底向下移动，而价带顶位置基本保持不变。由态密度可以看出(图3)，SnTiO3的导带底主要是由Ti 3pxy轨道提供，而其价带顶主要是由Sn 5s和O 2p(x,y,z)轨道共同提供。S掺杂后的SnTiO2.5S0.5导带底由Ti 3(dxy+dyz+dxz)轨道提供，此时的价带顶依然是S 5s轨道起到主要作用，但S的3px轨道也做出了一定的贡献，而O的轨道贡献减弱。此时，Ti 3d轨道的非占据态能量降低， SnTiO2.5S0.5导带底向低能级移动，能带带隙减少。从图3b中也可以看出，S与Ti和Sn在-1 eV和-4 eV有较强的杂化，这说明S与Ti和Sn充分成键。

Bader电荷分析表明，S的掺入使阳离子或者阴离子的电荷总数变小。不含S的晶胞单元离子电荷总数变化小，含S的晶胞单元离子电荷总数变化比较大，这是由于S的电负性要比O小，导致近邻S的离子展现的离子性要比远离S的离子做展现的离子性弱，离子之间的成键变弱。由于Sn被两个晶胞单元所共用，我们将离S近的Sn归入含S的晶胞单元，离S远的归入不含S的晶胞单元。如表3所示，不含S晶胞单元的每个离子的电荷变化都比较小，甚至不变；而含S晶胞单元的每个离子的电荷变化都比较大。SnTiO2.5S0.5比SnTiO3整体电离度的减少导致了其能带带隙变低[12]。

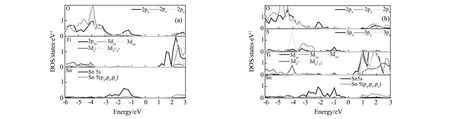
图3 态密度图 (a)SnTiO3;(b)SnTiO2.5S0.5 Fig.3 Density of states (a)SnTiO3;(b)SnTiO2.5S0.5

通过berry相方法[24]，计算得到了S掺杂前后的SnTiO3极化强度值(表1)。可以看出，计算得到纯SnTiO3的极化强度为1.15 C/m2，与其它理论值(1.28 C/m2)[20]符合的很好。随着S掺杂的增加，极化强度仍保持较大数值，且有明显增加。对于铁电光伏材料，较大的极化强度对于改善其光学性质具有非常重要的意义。

表3 SnTiO3-xSx (x=0, 0.5)的Bader 电荷。(SnTiO2.5S0.5)O和(SnTiO2.5S0.5)S 分别表示不含S和含S的Ti八面体所在晶胞单元。Oa/b和Oc分别表示不含S的八面体中与Ti平行和垂直的OTable 3 Bader charge analysis results for SnTiO3-xSx (SnTiO2.5S0.5)O和(SnTiO2.5S0.5)S represent the cell without and with S, respectively. Oa/b and Oc represent the parallel O and the vertical O to Ti octahedral without S

4 结 论

(1)当S掺入SnTiO3时，S更趋向于取代Site1位置的O，形成稳定的结构，S的掺入导致SnTiO3沿c轴拉伸，c/a比值变大。

(2)能带分析表明，掺入少量S可以使SnTiO3的带隙由纯SnTiO3的1.87 eV减小到1.01 eV，且当S掺杂量为x=0.33和0.5时带隙一样，均为间接带隙。态密度分析表明，S的掺入导致SnTiO2.5S0.5中的Fe 3d轨道非占据态能量降低，对导带底贡献增强，S与Ti和Sn成键对价带顶产生影响。Bader电荷分析表明，SnTiO2.5S0.5带隙比SnTiO3小是由于S的电负性要小于O的电负性，造成SnTiO2.5S0.5的整体电离度相对于SnTiO3变弱。

(3)Berry相计算极化强度显示，S的掺入使SnTiO3的极化强度变大，大的极化强度对SnTiO3作为铁电光伏材料具有积极意义。