基于子集一致性检测的诊断解极小性判定方法

田乃予 欧阳丹彤 刘 梦 张立明

(吉林大学计算机科学与技术学院 长春 130012) (符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012)

基于模型诊断(model-based diagnosis， MBD)是人工智能(artificial intelligence, AI)领域中一个十分活跃的研究分支，对整个AI领域的研究起着重要推动作用[1].其是为克服第1代诊断专家系统的严重缺陷而提出的智能推理方法，广泛应用于通信、网络、交通、电子设备、航天等诸多领域.

一方面，AI领域的其他分支(如知识表示、机器学习、约束求解等)中许多研究成果可以在MBD问题中得到应用，促进了MBD的发展.例如MBD问题与数据挖掘中的频繁项集挖掘和子句模式挖掘[2-3]中解的部分特征具有一定的相似性，许多方法策略可以互相应用，相互促进发展.另一方面，MBD的研究暴露了许多AI技术中存在的问题，激发了研究者的研究热情.例如可以利用MBD改进软件测试[4].

20世纪60年代，源自航天、军工等高可靠性工程的迫切需要，在AI领域逐渐形成了诊断推理这一研究热点.诊断一直是人工智能的一个挑战，在过去的20年中，研究主要集中于基于模型的诊断，通过利用模型代表物理系统的结构和行为来进行诊断.该方法通过建立真实系统对应的模型，利用系统输入得到系统的预期行为，然后以预期行为与观测行为的差异作为诊断算法的输入，进而计算能够解释这种差异的诊断解.

1987年首个MBD方法HS-tree (hitting-set-tree)方法由Reiter[5]提出.其结合Dekleer[6]提出的冲突集概念，通过求解电路所有极小冲突集的极小碰集得到整个电路的所有极小诊断解.虽然该方法保证了解的正确性，但却存在因剪枝而丢失正确解的可能.1989年Greiner等人[7]对此方法进行改进，提出了HS-DAG(hitting-set directed acyclicgraph)方法.之后国内外学者对间接求诊断方法，即基于冲突的诊断方法进行了大量研究，由于极小碰集求解是基于冲突的诊断方法的关键步骤，因此许多研究都集中于极小碰集算法.姜云飞等人[8]提出BHS-tree(binary-hitting-set-tree)方法，该方法基于HS-tree方法，利用枚举树结构求解极小碰集，即极小诊断解，解决了HS-tree算法剪枝丢解的情况，并且可以增量求解；赵相福等人[9]提出基于集合势的CHS-tree(cardinality-based hitting-set-tree)方法，每次选择当前集合簇中势最小的集合扩展，并结合集合簇中元素出现的频率，将大问题分解成子问题，进而得到不包含该扩展集合中各元素的集合簇的所有极小碰集；欧阳丹彤等人[10]提出基于动态极大度的极小碰集求解方法，提出未扩展元素度和结点度的概念，尽早生成集合簇的碰集，减少枚举树生成结点的个数，提高了求解效率.Jannach等人[11]通过并行化枚举树的结构计算碰集，更好地利用计算资源而不会丢失任何诊断解.

间接求解的诊断方法由于求解过程分为求极小冲突集和求极小碰集2个步骤，求解效率受到2部分所使用算法的共同制约.随着对MBD 问题研究的深入与计算机硬件的发展，许多学者对直接求解 MBD 的方法进行了研究[12].其中，基于SAT(satisfiability)的诊断方法吸引了大量研究者的关注.

SAT问题是首批被证明的NP-完全问题[13]，具有重要的理论和实用价值，长久以来吸引着国内外学者的关注，其求解过程的研究一直是人工智能领域的核心难题之一.近些年来对SAT问题的研究取得了很大的进步，很多已有算法得到了有效地优化改进，同时许多创新方法不断被提出.将MBD 问题转化为 SAT 问题进行求解，能够克服诊断问题复杂性不断增加的难题，因而得到众多学者的广泛关注[14].

Smith等人[15]首次提出了基于SAT求解的多故障诊断与定位算法，为之后基于SAT的模型诊断研究提供了基础.Metodi等人[16]提出把复杂的MBD预处理问题和SAT编译技术结合在一起的编译方法，进而达到简化合取范式(conjunctive normal form, CNF)的目的.之后，Metodi等人[17]提出基于求极小势诊断的新编译方法，该方法进一步对CNF进行了简化.Koitz等人[18]提出将故障信息转化为用于溯因模型诊断中的Horn子句，利用一个映射函数自动化建模过程.一些直接求解诊断方法和求极小碰集问题相似，都是元素对应超图中集合遍历问题.而由于超图数据结构复杂，在求解时多采用集合枚举树(set-enumerations-tree, SE-tree)[19]形式化方法遍历超图中的集合.赵相福等学者提出了基于枚举树的CSSE-tree(conflict-set based on set-enumerations-tree)[20]方法，将被诊断系统的模型和观测结果用CNF描述并利用 SAT求解器求取诊断解.欧阳丹彤等人[21]基于问题的结构特征，对CSSE-tree方法进行改进，有效地实现了对诊断的无解空间进行剪枝，并对部分集合枚举树从底层结点到根结点进行反向搜索，构建了LLBRS-tree(last-level based on reverse search-tree)方法.该方法减少了SAT求解次数，缩减了求解问题规模，是一种求解效率较高的方法.刘梦等人[22]在LLBRS-tree方法的基础上，使用电路分解并利用非故障输出子电路组件间组合形成的结点肯定不是诊断解的特性，缩减了问题规模，提出结合问题特征的分解式方法GD(grouped diagnosis)方法.刘伯文等人[23]提出电路分块诊断方法ACDIAG(abstract circuit diagnosis)方法，通过对电路分块缩减了电路规模，并利用LLBRS-tree方法对分块后的电路求解得到极小块诊断解；结合抽象电路的结构特征，利用诊断解拓展方法对极小块诊断解扩展得到原电路全部极小诊断解.

为保证最终得到诊断解是极小的，诊断解的极小性检测是求解基于模型诊断问题的关键步骤.之前的研究多集中于碰集极小性的研究，刘思光等人[24]提出基于元素独立覆盖度检测的碰集极小性判定方法ICC(independent coverage checking)方法并通过深入分析增量求解过程中非极小碰集的产生原因，给出ICC方法的增量判定形式IICC(incre-mental independent-coverage-checking)方法，提高了碰集求解的效率.王荣全等人[25]提出将碰集求解问题转换成SAT问题进行迭代求解，并给出结合元素覆盖集合度的极小化策略的高效极小碰集求解方法.碰集的极小化策略可应用于基于冲突的诊断方法.但目前研究多集中于更为高效的直接求解诊断方法.本文在对LLBRS-tree, GD, ACDIAG这3种方法充分研究的基础上，发现其使用的诊断解极小性检测方法存在的不足：原有极小性检测方法随着求解过程中得到的诊断解数量增多，检测难度逐渐提高，耗时也随之增大.若能对此进行优化，减小诊断解极小性检测过程的耗时，将对现有算法效率有所提高.针对此问题，本文提出一种基于子集一致性检测的诊断解极小性判定方法.该方法无需同已得到的诊断解进行比较，通过对得到的诊断解自身进行检测来判断其真子集中是否含有诊断解，进而进行极小性判定，避免了传统诊断解极小性检测方法的不足.该方法避免了求解过程中诊断解集合增大对效率的影响，进而提高了诊断算法的整体求解效率.

1 预备知识

本节将介绍基于模型诊断和SAT问题的相关概念及定义，同时给出使用SAT方法求解模型诊断问题过程中将问题对应的电路模型转化成CNF文件的方法.

1.1 基于模型的诊断

下面给出基于模型的诊断问题的相关定义.

定义1.诊断系统[5]. 一个MBD系统定义为一个三元组SD,COMPS,OBS，其中：

1)SD(system description)为系统描述，是一阶谓词公式的集合；

2)COMPS(system components)为系统的组成部件集合，是1个有限的常量集；

3)OBS(system observation)为观测集，是一阶谓词公式的有限集.

定义2.诊断问题[5].基于一个待诊断系统SD,COMPS,OBS，产生一个诊断问题，当SD∪{AB(c)|c∈COMPS}∪OBS不一致时.

定义3.诊断[5]. 基于一个MBD系统SD,COMPS,OBS，Δ⊆COMPS是一个诊断，当SD∪{AB(c)|c∈Δ}∪{AB(c)|c∈COMPS-Δ}∪OBS一致时.

定义4.极小诊断[5]. 基于一个MBD系统SD,COMPS,OBS，Δ⊆COMPS是一个极小诊断当且仅当不存在子集Δ′⊂Δ是一个诊断.

在系统的SD,COMPS,OBS所组成的观测行为与预期行为发生冲突之时诊断问题产生.基于模型诊断问题的目的是找到可以解释这种差异的诊断解.

1.2 SAT问题

SAT问题，一直以来都是理论计算机科学和人工智能领域的著名问题.给定一个布尔公式，求解SAT问题的目的是，确定是否存在一组变量赋值使得公式真值为真，若存在，需要返回一组满足条件的变量赋值.SAT问题在模型检验、逻辑电路优化等应用方面有着非常重要的作用.着眼于SAT问题的理论意义和实际应用价值，其相关研究已成为国内外热点之一.下面给出SAT问题的相关定义.

定义5.文字[16]. 给定n个布尔变量l1,l2,…,ln,0≤i≤n，其中li或li的否定称为文字.

定义6.子句[16]. 称文字用析取符号连接而成的公式为子句.

定义7.合取范式[16]. 将子句用合取符号连接而成的公式称为合取范式.

定义8.可满足不可满足[16]. 对某一CNF公式，如果存在使其公式计算值为真的变量赋值，则称该CNF公式是可满足的；反之，如果不存在这样的赋值，则称该CNF公式是不可满足的.

例1.给出CNF范式：

C={1:(a),2:(a),3:(a∨b),4:(b)},

C是不可满足的，因为子句1和子句2无法同时为真，同样也找不到一组赋值使子句1,3,4同时为真.

1.3 集成电路转化为CNF

3=1∧2,

3⟺1∧2,

(3→1∧2)(1∧2→3),

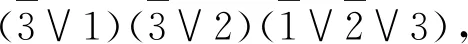
最终化简后的结果即是:

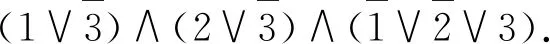
Fig. 1 Symbol of AND gate图1 与门符号

将系统的相应描述以CNF 文件的形式表示.主要包含电路逻辑和电路观测2部分.

CNF文件的格式为：CNF文件中每行为1个对应系统相关描述的子句，最后以0结尾.

以图2中国际标准测试电路ISCAS-85中的c17电路为例，电路逻辑对应的相关CNF 文件如图3所示.

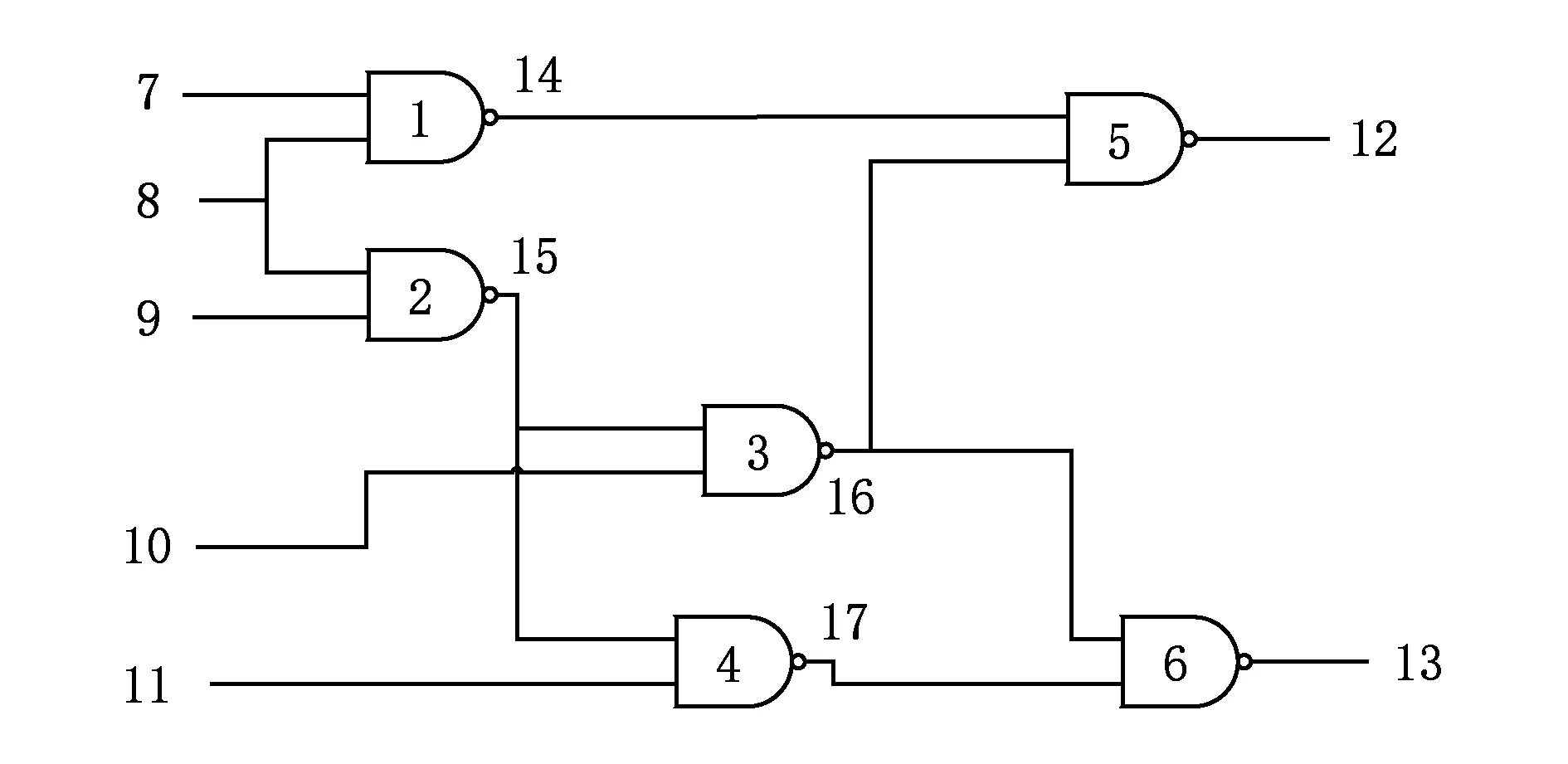
Fig. 2 Logic circuit of c17图2 c17逻辑电路

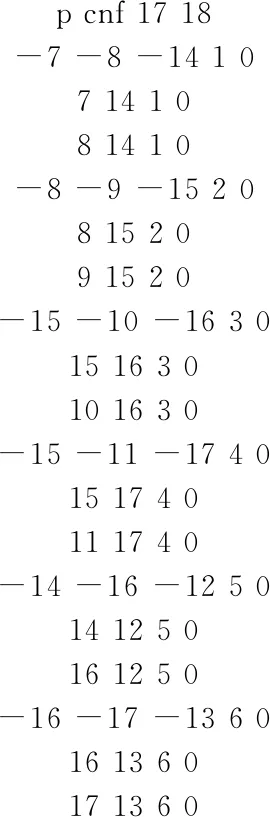
p cnf 17 18-7 -8 -14 1 07 14 1 08 14 1 0-8 -9 -15 2 08 15 2 09 15 2 0-15 -10 -16 3 015 16 3 010 16 3 0-15 -11 -17 4 015 17 4 011 17 4 0-14 -16 -12 5 014 12 5 016 12 5 0-16 -17 -13 6 016 13 6 017 13 6 0

Fig. 3 CNF file of c17
图3 c17逻辑电路对应的CNF 文件

图3中第1行p cnf 17 18表示该电路系统转化为CNF 文件格式后有17个变量、18条子句，p cnf为关键字.

将系统描述SD和系统观测OBS转换为CNF文件后，就可以作为SAT求解器的输入对待诊断系统进行求解.

2 MBD相关算法

本节将介绍基于模型诊断的相关算法，主要介绍LLBRS-tree方法以及基于该方法的优化：分解式GD方法和电路分块ACDIAG方法.这些方法都是目前效率较高的诊断求解方法，同时，它们都采用了相同的诊断解极小性检测方法.

2.1 基于SE-tree调用SAT的诊断方法

基于SE-tree调用SAT的诊断方法是将集合枚举树应用于MBD问题上，这种树模型可以以一种有结构的方式枚举出给定集合的幂集.

该方法对待诊断系统组件集COMPS对应的SE-tree进行遍历，同时对所遍历到的结点是否为诊断解进行判定，当遍历完成时，便可得到待诊断系统的所有诊断解.结点判定的基本思想是假设结点中的元件为故障并将其余元件都置为正常，将结点对应的单元子句加入到之前由系统描述SD和系统观测OBS转换而来的CNF文件中，作为SAT求解器的输入，进行一致性检测.若可满足，则该结点是一个诊断解，将此诊断解保存.

2.2 LLBRS-tree方法

LLBRS-tree方法对诊断的无解空间进行剪枝,并对部分集合枚举树从底层结点到根结点进行反向搜索.该方法减少了SAT求解次数，缩减了求解问题规模，是一种求解效率较高的方法.下面给出相关定义.

定义9.有解剪枝[21].在遍历某一待诊断系统组件集对应的集合枚举树时，对于树中的某一结点，其父结点或祖先结点如果是可满足的，即是诊断解.那么该结点一定不是极小诊断解，可以跳过对枚举树中此类结点的判断，称这一操作为有解剪枝.

定义10.无解剪枝[21].遍历一棵集合枚举树，对于树中的某一结点，其子结点或者子孙结点如果是不可满足的，即不是诊断解，那么该结点一定不是诊断解，跳过对枚举树中此类结点的判断过程，这叫做无解剪枝.

定义11.反向搜索[21].针对一棵集合枚举树，当已知枚举树的层数时，称从枚举树的最后一层向枚举树的根结点搜索的过程为树的反向搜索.

LLBRS-Tree方法主要是基于定义9～11，对集合枚举树以反向搜索的过程遍历，同时调用SAT求解器对树上的结点是否为诊断解进行判定：

1) 如果结点可满足，则对结点进行极小性检测，并根据检测结果对诊断解集进行相应操作.根据定义9，可以将该结点未访问的子孙结点减掉，即有解剪枝.第2步将判断该结点的父结点.

2) 如果结点不可满足.根据定义10，可以将该结点的父结点减掉，即无解剪枝.下一步判断该结点右边的结点.

LLBRS-tree方法利用有解剪枝和无解剪枝的策略，减小求解问题规模从而提高诊断求解效率.

2.3 GD方法

GD方法通过对电路进行分解并利用非故障输出子电路组件间组合形成的结点肯定不是诊断解的特性，缩减诊断问题规模，从而提高求解效率.

定义12.输出组件集[22]. 设某个待诊断系统可表示为SD,COMPS,OBS，称O⊆COMPS为输出组件集，当对于所有组件c∈O，其输出为该待诊断系统的输出.

定义13.故障输出组件集[22]. 设某个待诊断系统可表示为SD,COMPS,OBS，称ABCompS⊆O是故障输出组件集，当组件c∈ABCompS的输出是该待诊断系统的故障输出.

定义14.可达通路[22]. 诊断问题中，组件c1到组件c2有可达通路表示组件c1到电路输出的路径上经过组件c2，此时path(c1,c2)为真.

定义15.故障输出子电路组件集[22]. 设某个待诊断系统可表示为SD,COMPS,OBS，其中故障输出组件集ABSubCircuitCompS⊆COMPS是一个故障输出子电路组件集,当{c|c∈ABCompS∨path(c,c0)}，其中，c0∈ABCompS.即子电路中组件c是ABCompS中组件或者到ABCompS中某一组件有可达通路.

GD方法根据输出观测与预期的差异，将输出分为故障输出与非故障输出.以此为条件对电路进行分解，分为故障输出子电路和非故障输出子电路.

对于非故障输出子电路组件，由于非故障输出子电路组件集中的任意元素组成的集合不可能是诊断解，因此GD方法将非故障子电路集中的组件放在待枚举元素的后半部分，并将其对应的子树剪掉.而故障输出子电路组件则使用枚举树并利用LLBRS-tree算法进行求解.

GD方法结合问题特征和电路逻辑电路组件进行分解，缩减问题规模，进而减少求解过程中调用SAT求解器的次数，提高诊断求解效率.

2.4 ACDIAG方法

ACDIAG方法是对电路进行抽象分块来缩减电路规模的高效诊断算法.

定义16.起始元件[23]. 对于一个待诊断系统，称满足3个条件之一的元件为起始元件：

1) 元件为系统输出元件；

2) 元件的输出是2个或2个以上元件的输入；

3) 元件是多输入元件，即元件输入端个数大于2.

结合电路结构特征，给出对电路的分块规则[23]：

1) 找出电路中所有起始元件a1,a2,…,ak即将电路划分为k块；

2) 对每个起始元件ai(1≤i≤k)进行拓展，若元件b的输出作为元件ai的输入，并且元件b不是起始元件，则将元件b扩展到ai所代表的分块中.

以此分块规则得到的抽象电路，每个子电路块有且仅有一个输出，并且由该输出元件代表.

ACDIAG方法利用LLBRS-tree方法对分块后的抽象电路求得极小诊断解，称作极小块诊断解.再利用诊断解拓展方法，对极小块诊断解进行拓展，从而得到原电路的全部极小诊断解.

ACDIAG方法前期通过缩减电路规模减少了利用LLBRS-tree方法求取诊断解的时间，再利用拓展方法得到全部解，实验表明其拓展所需时间远小于极小块解求解时间，因此大大提高了求解效率.

3 诊断解极小性判定过程

3.1 原有诊断解极小性判定过程

判定诊断解的极小性是MBD相关算法中至关重要的一步.根据定义4可知，Δ是一个极小诊断当且仅当不存在子集Δ′⊂Δ是一个诊断，即不存在Δ的任何真子集也是待诊断MBD系统的一个基于一致性诊断.极小性判定过程必须基于此定义.下面给出LLBRS-tree方法极小性判定过程的具体方法，GD方法和ACDIAG方法是基于LLBRS-tree方法的，其极小性判定过程也应用了相同的方法.

算法1.诊断解极小性检测算法.

函数:MinialDiag_Checking(Diag,DigRes)

输入:诊断解Diag、极小诊断解集合DigRes={Diag1，Diag2，…，Diagn};

输出:极小诊断解集合DigRes.

Begin

① for (i=1;i≤n;i++)

② ifDiag⊂Diagi

③DigRes.Remove(Diagi);

④ end if

⑤ else ifDiagi⊆Diag

⑥ return;

⑦ end if

⑧ end for

⑨DigRes←DigRes∪{Diag};

End

在这一过程中，被检测为诊断解的组件集作为输入，若在已有诊断解集中发现新得到诊断解的真超集，则说明该超集必不为待诊断系统的极小诊断解将其从极小诊断集中删去(行③);若发现新得到诊断解的子集，则新得到诊断解必不是极小诊断，将该解丢弃，结束比较过程(行⑥);若比较过程结束时都未发现新得到诊断解的真子集，则将该诊断解暂时加入极小诊断解集中(行⑨).

当对集合枚举树的遍历结束时，即诊断求解算法终止时，极小诊断解集中保留的诊断解即是待诊断系统的全部极小诊断解.需要注意的是，在算法运行的过程中，极小诊断解集中保留的诊断解并不一定是极小的，即可能保留了大量冗余解.

这种方法存在的主要问题是，极小诊断解集的规模会随着诊断求解算法的进行而不断变大，新得到诊断解的极小性判定时间也会随之增加.因为每当得到一个新的诊断解，都需要将它与极小诊断解集中部分甚至全部诊断解进行比较.由于此方法的耗时往往与诊断解集的大小正相关，当问题后期诊断解集规模较大时，使用此极小性判定方法逐一比较会带来较多的时间开销，影响求解效率.而下面提出的基于子集一致性检测的诊断解极小性判定方法则避免了此问题.

3.2 基于子集一致性检测的诊断解极小性判定方法

本文提出的基于子集一致性检测的诊断解极小性判定方法完全遵循定义4，即如果一个诊断解的所有真子集都不是诊断解，那么这个诊断解就是关于MBD系统的一个极小诊断解.为避免3.1节所给出的传统诊断解极小性判定过程存在的不足，基于子集一致性检测的诊断解极小性判定方法在求得诊断解之后仅针对诊断解自身进行检测，即检测其真子集中是否含有诊断解，按照此方法加入诊断解集合中的诊断解全部是极小的，避免了比较的过程.

对已求得诊断解的所有真子集进行判断，可以检查其真子集中是否含有诊断解，但如果对每个子集进行检测，则调用SAT求解器次数过多，会消耗较多的时间，而我们可以利用SAT求解器判定某一状态下系统逻辑和观测行为的一致性来达到同样的目的.下面首先给出算法2来介绍如何利用SAT求解器来判断一个组件集合是否是待诊断系统的诊断解.

算法2.诊断解判断算法.

函数:Is_Sol(ps[])

输入:待判定组件集ps、系统描述文件SD.cnf、系统观测文件OBS.cnf；

输出:bool类型值(如果组件集ps是系统的诊断解，则返回1;否则返回0).

①SD.cnf.add(clause∈OBS.cnf);

②SD.cnf.add(ps中每个组件对应的反常单元子句);

③SD.cnf.add(COMPS-ps中每个组件对应的正常单元子句);

④isSAT←SATsolver(SD.cnf);

⑤ ifisSAT=SAT

⑥ return 1;

⑦ else

⑧ return 0;

⑨ end if

算法2首先将系统观测文件OBS.cnf中的子句加入到表示系统描述的SD.cnf文件中(行①).对于待判定的组件集合ps中的组件，将其对应的反常单元子句即用正文字描述，加入到SD.cnf文件中(行②)，以此假设这些组件均是故障组件.对于系统组件集中除去待判定组件集的剩余元素，使用负文字描述，即将COMPS-ps中每个组件对应的正常单元子句加入到SD.cnf文件中(行③)，以此假设这些组件均是非故障组件.例如假设系统总共有7个组件COMPS={C1,C2,C3,C4,C5,C6,C7}，待判定组件集ps={C1,C2,C3,C4}时，那么加入系统描述SD.cnf文件中的子句应为：

1 0

2 0

3 0

4 0

-5 0

-6 0

-7 0

然后调用SAT求解器对SD.cnf文件进行可满足性判断.如果可满足，则表明在组件集ps中的组件均为故障组件而COMPS-ps中的组件均为正常组件的情况下，系统当前的观测行为是可以解释的.根据诊断解的定义可知，组件集ps是诊断解，返回1;否则，组件集ps不是诊断解，返回0.

以此为基础，我们发现可以利用SAT求解器检查组件集ps是否存在为诊断解的真子集.

定理1.设某个待诊断系统可表示为SD,COMPS,OBS，Sub⊆COMPS为该MBD的一个诊断解，如果∃S∈Sub，且SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}是一致的，则∃Sub′⊆Sub-{S}为待诊断系统的诊断解.

证明.

反证法.假设:

SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}是一致的；且不存在Sub′⊆Sub-{S}为待诊断系统的诊断解.

Sub为已知为诊断解，如果不存在Sub′⊆Sub-{S}为诊断解，则说明若存在为Sub真子集的诊断解，该诊断解中必包含S，那么:

SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}不能推出一致，即假设S组件为正常同时限定诊断解为Sub真子集的情况下是无法解释当前系统的行为.此时:

SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}是不可满足的.与上述条件矛盾，因此假设不成立.

证毕.

定理2.设某个待诊断系统可表示为SD,COMPS,OBS，Sub⊆COMPS为该MBD的一个诊断解，如果对∀S∈Sub，SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}是不一致的，则Sub为待诊断系统的极小诊断解.

证明.

因为对于S∈Sub，如果：

SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}是不一致的，根据定理1可以得到不存在Sub′⊆Sub-{S}.所以如果对于:

∀S∈Sub，SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}都是不一致的，则可说明不存在Sub′⊂Sub为诊断解，根据极小诊断的定义可证得Sub为待诊断系统的极小诊断解.

证毕.

基于定理1与定理2，给出利用SAT求解器进行基于子集一致性检测的诊断解极小性判定的算法3.

算法3.基于子集一致性检测的诊断解极小性判定算法.

函数:Is_MinimalSol(diag[])

输入:诊断解diag={D1,D2,…,Dn}、系统描述文件SD.cnf、系统观测文件OBS.cnf；

输出:bool类型值(如果诊断解diag是系统的极小诊断解，则返回1;否则返回0).

①SD.cnf.add(clause∈OBS.cnf);

②SD.cnf.add(COMPS-diag中每个组件对应的正常单元子句);

③ for (j=1;j≤n;j++)

④CNF←SD.cnf;

⑤CNF.add(Dj对应的正常单元子句);

⑥isSAT←SATsolver(CNF);

⑦ if (isSAT=SAT)

⑧ return 1;

⑨ end if

⑩ end for

算法3可针对已知诊断解进行子集一致性检查，输入是通过算法2判定为诊断解的组件集.同算法2一样，需将系统的观测文件OBS.cnf中的子句添加到系统描述文件SD.cnf中(行①).依据定理1，对于已知诊断解diag中的每个组件，依次将它们与COMPS-diag中所有组件对应的正常单元子句加入到表示系统描述和观测的CNF文件中，以此假设它们都是非故障组件.之后，调用SAT求解器判定CNF文件的可满足性，对应定理1中判定:

SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}是否一致，从而判断这种假设能否解释当前系统的行为，即检查子集的一致性(行②～⑥).如果可满足，则说明存在diag′⊆diag-Dj为诊断解，即诊断解diag的真子集中存在诊断解，根据定义3可知诊断解diag不是待诊断系统的极小诊断解，跳出循环，算法结束(行⑦～⑩).依据定理2可知，如果循环结束没有找到diag的真子集为诊断解，即对应定理2中对于∀S∈Sub，SD∪OBS∪{AB(c)|c∈{S}∪(COMPS-Sub)}都是不一致的，则可以判定diag为待诊断系统的极小诊断解(行).

例2.假设系统总共有7个组件COMPS={C1,C2,C3,C4,C5,C6,C7}，已知组件集diag={C1,C2,C3,C4}是诊断解时，我们需要加入到表示系统描述和观测的CNF文件中的子句为：

1) -1 0

-5 0

-6 0

-7 0

以此假定组件C1,C5,C6,C7为非故障组件.之后调用SAT求解器，判断一致性，如果是可满足的，则表明{C2,C3,C4}的子集中有诊断解，那么组件集{C1,C2,C3,C4}必不是极小诊断解，算法结束.否则，继续将子句依次加入到CNF文件中并依次检查CNF文件的可满足性：

2) -2 0

-5 0

-6 0

-7 0

3) -3 0

-5 0

-6 0

-7 0

4) -4 0

-5 0

-6 0

-7 0

如果依次调用SAT求解器检测加入以上子句的CNF文件，均为不可满足，则表明组件集{C1,C2,C3,C4}的真子集中没有诊断解，诊断解{C1,C2,C3,C4}是待诊断系统的极小诊断解.

下面给出一个实例来阐述算法3的执行过程.

例3.以图2中国际标准测试电路ISCAS-85中的c17电路为例，该电路有6个组件COMPS={1,2,3,4,5,6}均为与非门，假设当前输入观测点“7”，“8”，“9”，“10”，“11”的观测值分别为高电平、高电平、低电平、高电平、低电平.输出观测点“12”，“13”的观测值为低电平、高电平.则系统观测的CNF文件描述如下：

7 0

8 0

-9 0

10 0

-11 0

-12 0

13 0

因观测行为与预期行为冲突，产生诊断问题.设已得到诊断解diag={1,3,6},需检测其极小性.根据算法3，依次加入3组子句到表示系统描述和观测的CNF文件中：

1) -1 0

-2 0

-4 0

-5 0

2) -3 0

-2 0

-4 0

-5 0

3) -6 0

-2 0

-4 0

-5 0

分别调用SAT求解器依次检测加入以上子句的CNF文件，均为不可满足，则根据定理2，可知组件集{1,3,6}的真子集中没有诊断解，即组件集{1},{3},{6},{1,3},{1,6},{3,6}均不是诊断解，诊断解diag={1,3,6}是该系统的极小诊断解.

算法3避免了算法1随着极小诊断解集规模的增大而导致诊断解极小性检查耗时大幅增加的问题.通过针对已知诊断解子集一致性进行判断，检测其真子集中是否含有诊断解来进行极小性判定.同时，该方法调用SAT求解器的次数与待检测诊断解中包含组件的个数线性相关，比对该诊断解全部真子集进行检测要少得多.

复杂性.假设待检测诊断解包含组件个数为n，当前已有诊断解个数为m. 算法3，即SCD(subset consistency detection)方法在最坏情况下最多需调用n次一致性检查.而传统极小性判定方法则需将此诊断解与m个诊断解判定子集关系，其复杂度为nm.

当m较大时，SCD方法复杂性明显低于传统极小性判定方法.而MBD问题随着求解过程的进行，m必不断增大，因此SCD方法的求解效率优于传统方法.

完备性.本文提出的子集检测方法针对的是求得的诊断解的极小性判定，不影响求解过程，因此不会存在丢解的情况，最终得到的是待诊断系统的全部极小诊断解.

因此，我们给出的方法不仅避免了原有方法的不足，同时也尽最大可能地减少了判定过程中SAT求解器的调用次数，最大程度上降低了诊断解极小性判定过程的耗时.

4 实验结果

本部分对SCD方法的有效性进行实验测试.将SCD方法应用于目前求解效率较高的GD方法和ACDIAG方法，并分别与应用原有诊断解极小性检测方法的GD和ACDIAG方法进行对比,进而对SCD方法的实验数据进行分析.采用的实验环境为Intel®CoreTMi5-3470 CPU@3.20 GHz，Ubuntu 64位系统.

对于GD方法和ACDIAG方法以及SCD方法的诊断解极小性判定过程，调用开源SAT求解器Picosat[26]进行可满足性检测.

本文的测试用例来源于国际标准测试电路ISCAS-85，包含了电路c17,c432,c499,c880,c1355,c1908.时间限制为172 800 s(48 h)，超出此时间记为TO.

表1给出SCD方法应用于GD方法的实验结果对比，表格第1行的l表示所求诊断解的长度；第1列表示测试所用电路实例；num表示求得诊断解个数.SCD与GD列分别表示将SCD方法应用于GD方法与原始GD方法求解耗时.可以看出对于较简单电路如c432,c499,c880,当极小诊断长度小于等于3时，应用原有诊断解极小性检测方法的GD方法与应用SCD方法的所用时间并无明显差别.但当所求诊断长度达到4时，应用SCD方法的GD方法求解效率开始有明显提高，以c432电路表现尤为明显，求解时间缩短近50%，对c499和c880电路的求解效率也均有不同程度的提高.当所求诊断长度达到5时，应用SCD方法的优势更为明显，在原有算法无法在限制时间内得到结果的情况下，应用SCD方法可以求得诊断解.而对于较复杂的c1355和c1908电路，当诊断解长度达到3时，算法效率就已有一定提高.当所求诊断解长度较小时，诊断解个数较少，应用原有极小性检测方法逐一比较的次数也较少，耗时不多，因此2个方法求解效率基本相同.当所求诊断长度较大时，随着算法运行生成的诊断解个数逐渐增多，极小诊断解集规模不断增大.此时，采用原有极小性检测方法，每当得到一个诊断解，都需要将它与极小诊断解集中部分甚至全部诊断解进行比较，使得极小性检测过程较为耗时.而应用SCD方法则可避免此问题，只需调用SAT求解器对新求得的诊断解子集一致性进行判定，在保证了每个加入极小诊断解集中的诊断解都是极小的同时，不用增加额外比较耗时，因此算法效率得到了提高.

我们也将SCD方法应用于ACDIAG方法进行了实验，实验结果对比如表2所示，SCD与ACD列分别表示将SCD方法应用于ACDIAG方法与原始ACDIAG方法求解耗时.可以看出SCD方法应用于ACDIAG方法同样是有效果的.ACDIAG方法是将复杂电路抽象为较简单电路进行求解，得到抽象电路的极小诊断后拓展得到全部诊断解，而SCD方法应用于抽象电路求得极小诊断解这一过程.因为是已简化的抽象电路，前期求得诊断解个数较少，所以当极小诊断长度≤4时，应用SCD方法的ACDIAG方法与原始ACDIAG方法的效率基本无明显差别，但对于较复杂电路c1355,当诊断长度达到4时，算法效率已提高40%;对于较简单电路如c432,c499电路当诊断长度达到5时，算法效率提高了50%左右.这反映出传统诊断解极小性检测方法存在的问题：对极小诊断解集规模较为敏感,而SCD方法避免了这点不足.因此，随着诊断解数量不断增多，本文提出的SCD方法的优势逐渐显现.

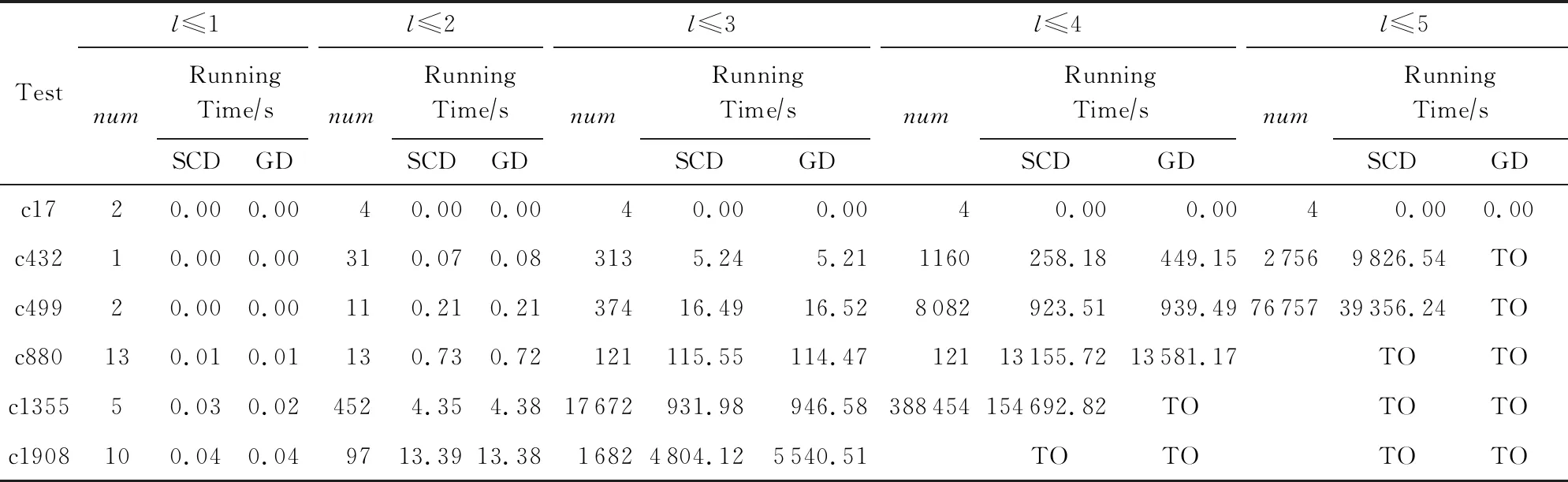
Table 1 The Running Time of SCD Method Based GD表1 基于SCD方法的GD方法运行时间对比

Note: The time limit is 172800s (48 h). Timeout is denoted as TO.

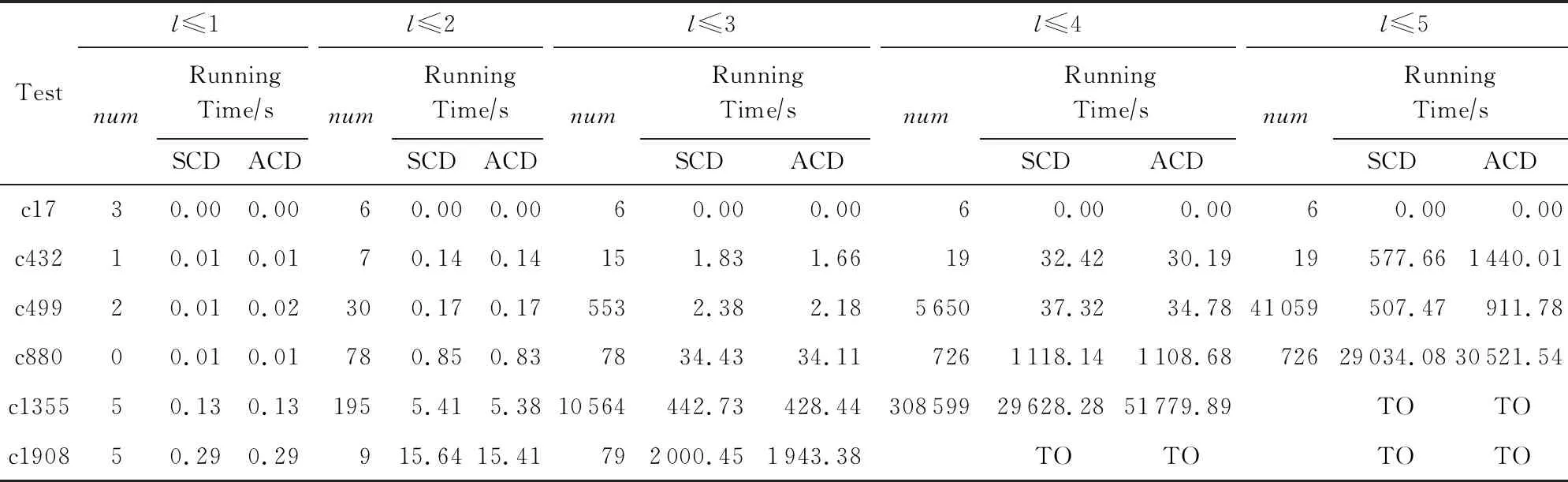
Table 2 The Running Time of SCD Method Based ACDIAG表2 基于SCD方法的ACDIAG方法运行时间对比

Note: The time limit is 172 800 s (48 h). Timeout is denoted as TO.

表1、表2的实验对比结果可以体现出SCD方法的有效性.本文以GD和ACDIAG方法为例，将SCD方法应用于这2个目前较高效的方法，算法效率均得到了一定的提高.实验结果也与我们提出的改进思想吻合，当所求诊断长度越长时，应用SCD方法对算法效率的提升也就越大.

5 结束语

在人工智能领域，基于模型诊断问题的研究一直备受中外学者的关注.本文通过对诊断解的极小性与该诊断解子集关系的研究，提出基于子集一致性检测的诊断解极小性判定方法——SCD方法.该方法通过对已知诊断解的部分子集进行一致性检测，从而给出诊断解的极小性判定，避免了原有方法诊断解之间的比较过程，减少了诊断解极小性检查过程的耗时.且SCD方法可应用于多个目前效率较高的基于模型诊断求解算法，如GD和ACDIAG方法.通过实验对比，针对不同电路，应用SCD方法的诊断方法求解效率均有明显提高，最高可提高约50%，并且由于传统诊断解极小性检测方法存在对诊断解集规模较为敏感的问题，随着所求诊断解长度的增加，SCD方法带来的优势将更加显著.