基于相似模型试验的简支箱梁振动传递特性研究

2019-07-12汪振国雷晓燕欧开宽张新亚

铁道学报 2019年5期

罗锟，汪振国，雷晓燕，欧开宽，张新亚

(华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013)

随着高速铁路和城市轨道交通路网密度的持续增加以及运营速度的逐步提高，其引起的环境振动与噪声问题日益严重。在高速铁路与城市轨道交通中占有较大比例的桥梁结构，其在交通荷载作用下产生的结构噪声具有频率低、衰减慢和影响范围广等特点，长期处于该环境中工作、生活将给人体造成一定危害[1-2]，因此对桥梁结构振动特性展开研究，探索结构噪声产生根源，并寻求减振降噪控制措施，具有重要的理论价值和工程意义。

桥梁结构振动特性研究中，文献[3]建立了大跨度公铁两用斜拉桥的有限元分析模型，将列车荷载以移动荷载的方式输入，分析了列车运行下桥梁纵向振动特性，并考虑黏滞阻尼器的设置对纵向振动的影响；文献[4]针对铁路高架桥梁，建立高架轨道系统有限元模型，重点分析了扣件刚度、结构阻尼等参数对高架轨道系统振动的影响；文献[5]建立了无砟轨道-高架桥的耦合解析模型，研究了系统参数对高架桥结构振动特性的影响；文献[6-7]运用有限元方法，建立了无砟轨道-箱梁结构耦合模型，并以速度及位移导纳为指标，分析了振动在箱梁结构中的传递特性，并探讨了箱梁截面形状、扣件刚度等参数对箱梁振动特性的影响。

可以发现，已有文献大多是通过数值模拟的方法来研究桥梁结构的振动特性，而采用模型试验研究该问题的文献较少。模型试验是验证与修正理论模型的有效方法之一，也是工程中解决复杂问题的重要手段[8-10]。此外，因研究目的不同，学者针对桥梁结构传递特性的探讨也缺乏全面性。混凝土箱梁结构在行车荷载作用下，与噪声辐射相关的结构振动主要集中在20～200 Hz[11]，然而在这一频率范围内，国内外针对桥梁结构振动传递特性的研究鲜有文献报道，且尚无针对性的试验研究。因此，本文以32 m简支箱梁为原型，设计制作了研究桥梁结构振动特性的简支箱梁模型(原型与模型间的几何相似比为10∶1)，并在验证模型正确性的基础上，通过锤击试验，研究箱梁振动在各板件之间和纵向上的传递特性，分析不同支座刚度对箱梁振动特性的影响。

1 模型试验相似理论

1.1 相似条件

为保证动荷载作用下的原型结构与模型相似，需满足以下条件[12]：

(1)几何相似。模型的几何形状必须与原型结构保持一致，不能随意改变和简化，且尺寸需呈一定比例，即

lp/lm=λl

(1)

式中：l为几何尺寸(下标p和m分别为原型和模型，下同)；λl为几何比(λ的下标表示相应物理量的相似比，下同)。

(2) 结构物理性能相似，包括质量、密度相似，即

(2)

式中：M为质量；ρ为密度。

(3) 运动相似。荷载作用下的速度和加速度响应保持相似关系，且时间亦符合相似要求，即

(3)

fp/fm=tm/tp=1/λt=λf

(4)

式中：v为速度；a为加速度；t为时间；f为频率。

(4) 动力相似。在动荷载作用下，结构上的任一作用力均应保持相似，即

Fp/Fm=λF

(5)

式中：F为作用力。

在动力作用过程中，对结构的动力性质产生影响的有重力、惯性力、弹性恢复力及其他外作用力，它们相应的作用力相似比如下:

重力

(6)

惯性力

(7)

弹性恢复力

(8)

式中：E为弹性模量。

其他作用力，令其相似比为Pp/Pm，则

Fp/Fm=Pp/Pm

(9)

由式(4)～式(8)得

(10)

对比分析相似4条件可知：相似条件(1)～(3)中的λl、λρ和λt相互独立，而条件(4)则限制了三者之间的关系。在缩尺模型制作时，不可能完全满足式(10)的要求，因此需在具体的研究过程中，根据研究目的和要求合理取舍，使原型和模型之间近似或部分地满足式(10)的要求。通常，模型试验相似分为弹性相似、重力相似和弹性-重力相似，当研究结构在弹性阶段的振动行为时，适用弹性力相似律[12-13]。

1.2 弹性力相似律

弹性结构振动方程

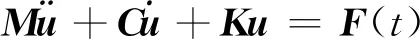
(11)

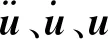
式(1)表明，影响结构振动的主要作用力为惯性力、阻尼力与弹性恢复力。在研究结构振动特性时，可主要保持惯性力与弹性恢复力相似，由式(7)、式(8)、式(10)可得

(12)

整理得

(13)

当研究结构在弹性阶段的动力响应时，还应保持作用力F相似，由式(10)得

(14)

此外

λK=(Fp/up)/(Fm/um)=λF/λu

(15)

式中：u为F作用下的位移；λl=λu。

由此可见，当研究结构弹性阶段的振动特性时，材料的弹性模量、密度和几何尺寸三个参数相互独立。因此，在模型试验设计时，模型材料选择可以更加灵活，这将使模型制作更加便捷。

2 箱梁相似模型设计与制作

2.1 原型箱梁

京沪高速铁路中桥梁占比85%以上，且多为32 m简支箱梁。因此，以京沪高速铁路32 m简支箱梁为研究对象，其桥面宽度12 m，梁高3.05 m，梁体采用C50混凝土浇筑，截面参数见图1。

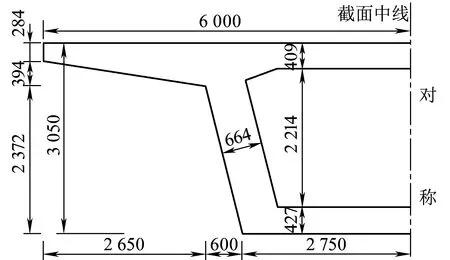
图1 原型箱梁截面(单位：mm)

2.2 缩尺箱梁

为减少制作误差对试验结果的影响，缩尺箱梁与原型箱梁间的几何相似比设为1∶10。缩尺箱梁制作时，混凝土选用自密实混凝土(H60-Ⅲ型)，纵向钢筋选用φ4碳素钢丝，箍筋采用2 mm普通钢丝，同时忽略预应力的影响。待缩尺箱梁养护成型后，采用应变法进行弹性模量测试，见图2，试验结果为Em=30 GPa。同时，实测12组混凝土试块的质量和密度，得到箱梁平均密度为ρm=2 203 kg/m3。制作完成的缩尺箱梁见图3。

图2 弹性模量试验

在测得缩尺箱梁实际参数后，根据原型箱梁与缩尺箱梁间的各参数相似关系，可得两者间各物理量的实际相似比，结果见表1。

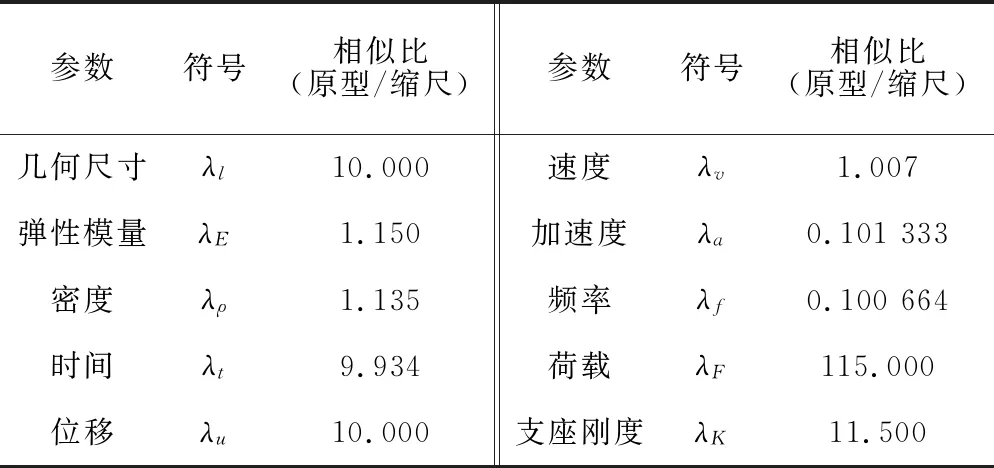
表1 原型箱梁与缩尺模型间的实际相似比

2.3 支座的模拟

选择3种不同规格的橡胶材料，见图4，按照钢板+橡胶材料+钢板的结构，制作不同刚度的箱梁支座：支座A、支座B和支座C。三种支座的抗压刚度值利用自制装置进行测量，见图5，测试装置包括：千斤顶、橡胶材料、夹板1、夹板2和压力传感器等。

图5 橡胶材料的抗压刚度试验

测试时，利用夹板1和夹板2夹紧橡胶材料，且在夹板上下分别固定加载装置千斤顶和压力传感器并对齐，位移传感器固定在上顶面和夹板之间用于橡胶压缩量的监测。正式加载前，位移传感器探针先预压10 mm。每组橡胶材料的刚度试验共进行3次。试验完成后，通过对数据的统计分析，在弹性范围内拟合压力和位移的线弹性关系，即可得到橡胶材料的刚度值，取3次试验结果的平均值作为该组支座的刚度值，结果见表2。

表2 橡胶材料抗压刚度

3 箱梁相似模型校验

3.1 相似比验证

根据原型箱梁和缩尺箱梁的实际参数，利用有限元方法建立原型箱梁和缩尺箱梁的数值计算模型，并进行模态分析，计算模态频率，求解两者之间的频率比，验证其是否满足上文理论推导结果。建模时，原型箱梁和模型箱梁的相同构件，均采用相同的单元进行模拟，并施加相同约束方式。前5阶模态频率计算结果见表3。

从表3可以看出，模态频率比的理论值与实际值间的误差在0.01%～0.03%。因此，可初步认为理论计算结果正确。

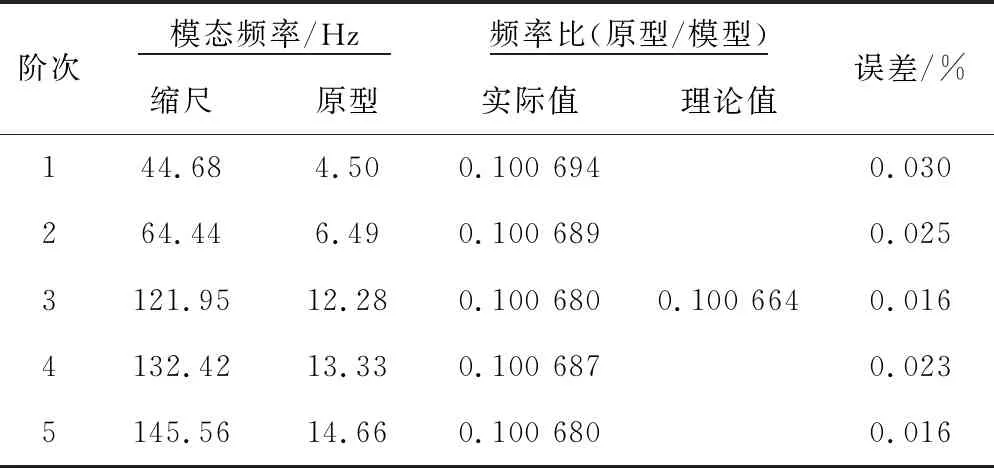
表3 各阶频率比理论值与实际值比较

3.2 模态试验

采用模态试验方法，进一步验证本文中设计制作的缩尺箱梁与原型箱梁具有相似性。为使结果具有可对比性，试验中的缩尺箱梁与有限元模型采用相同的约束方法，即固结。缩尺箱梁与桥墩的连接点见图6。

图6 支座处的约束方式

试验设备包括：西门子公司的LMS振动数据采集与分析系统(SC05数据采集系统，A/D 24位；LMS TEST.Lab分析系统，包括MIMO FRF Testing模块等)、PCB三向加速度传感器、力传感器、激振器、功率放大器及连杆等。试验中，首先通过测试系统输出随机猝发信号，并经功率放大器放大传至激振器激振，同时，利用力传感器和加速度传感器实时采集力信号和模型箱梁各拾振点上的加速度信号。再利用PolyMAX模态参数估计法对数据结果进行分析，最终得到模型箱梁的模态频率和模态振型。模态测试流程见图7。

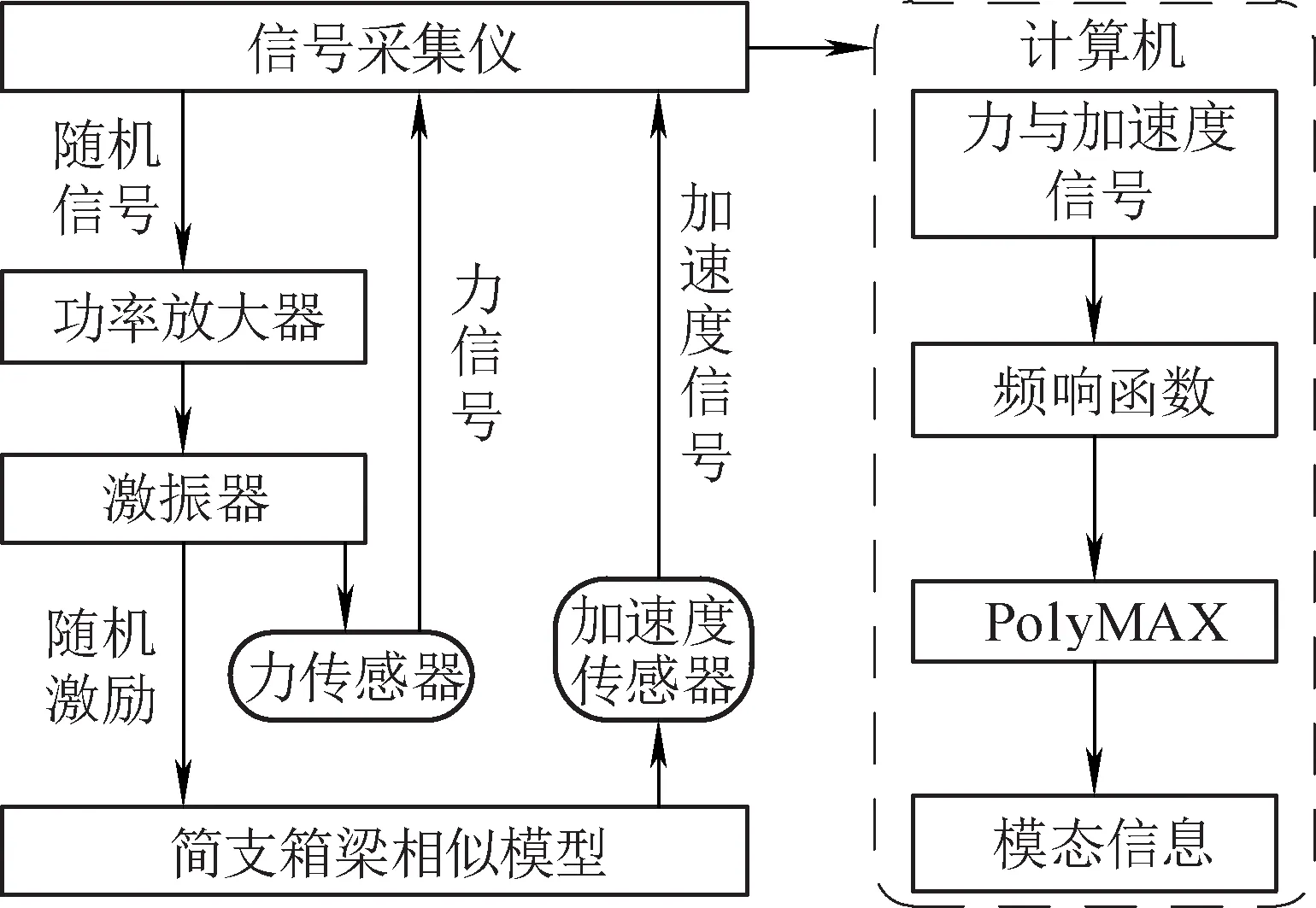
图7 模态测试流程

为确保结果的准确性，模态试验中沿模型箱梁长度方向，每0.4m选择一个测试断面，共9个测试断面，每个断面在顶板、腹板和底板位置设置8个拾振点，共72个测点。另外，激振点设置在箱梁角点，从下往上激振。具体布置见图8。图中：S1～S8为任一断面的8个拾振点；J1为激振点(箱梁角点)。

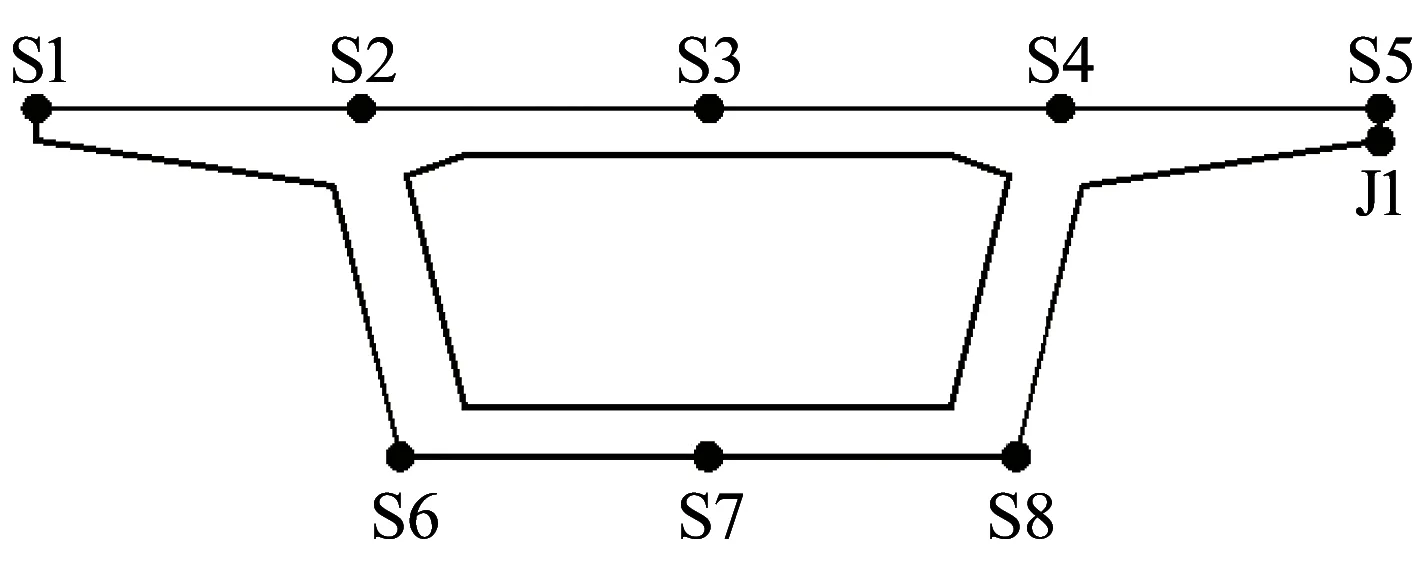
图8 激振点与拾振点位置

经PolyMAX模态参数估计法对数据进行分析后，在0～1 024 Hz共识别缩尺箱梁模型的60阶模态，其中前5阶模态的置信度矩阵见图9。

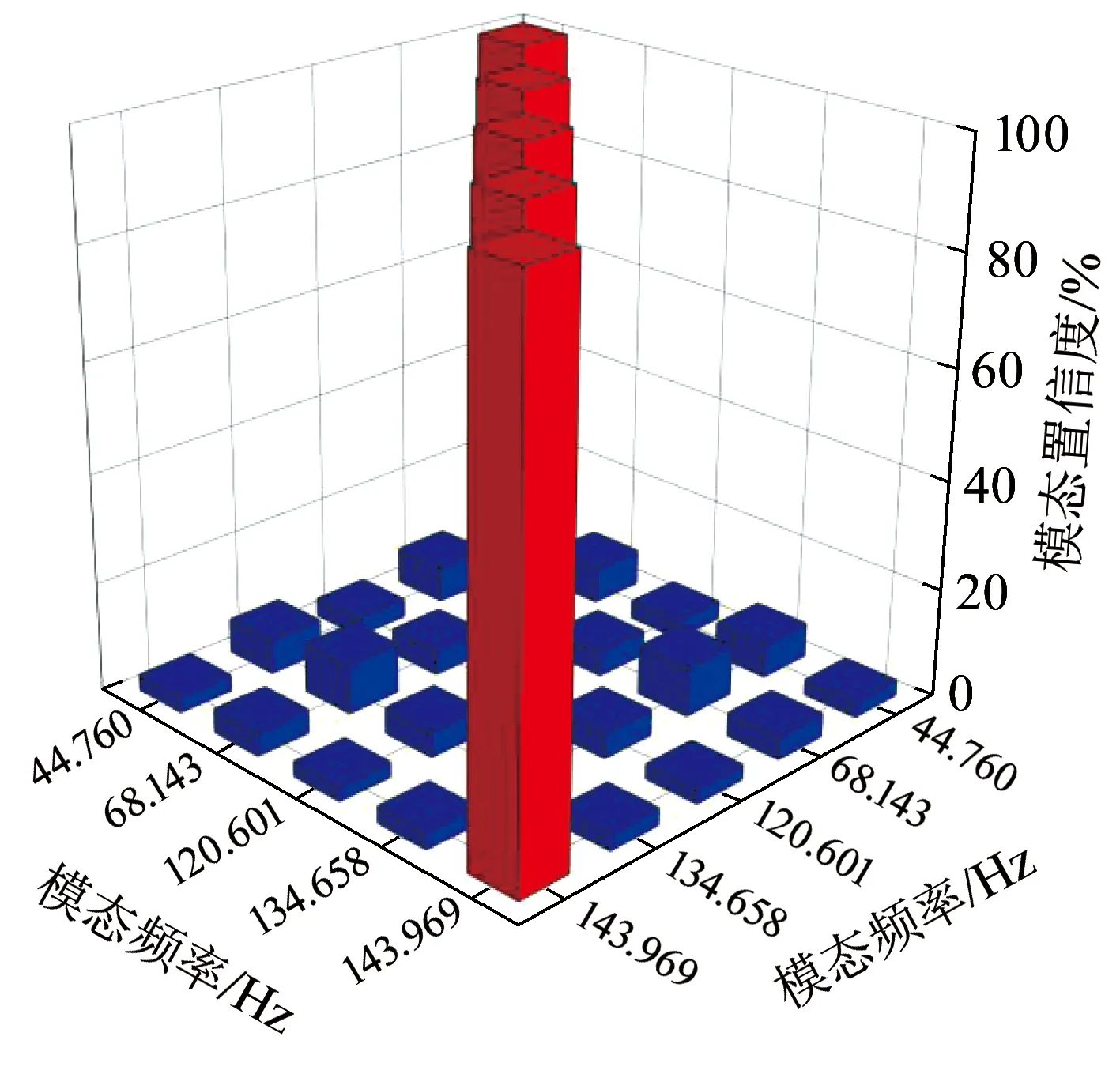
图9 前5阶模态的MAC图

由图9可知：矩阵对角线上的值均为100%，而非对角线位置的值均在10%以下，最大值仅为9.184%，因此前5阶模态相互独立。选其与有限元结果进行对比，其模态频率和模态振型对比见表4和图10。图10中，左列为有限元计算结果，右列为试验结果。

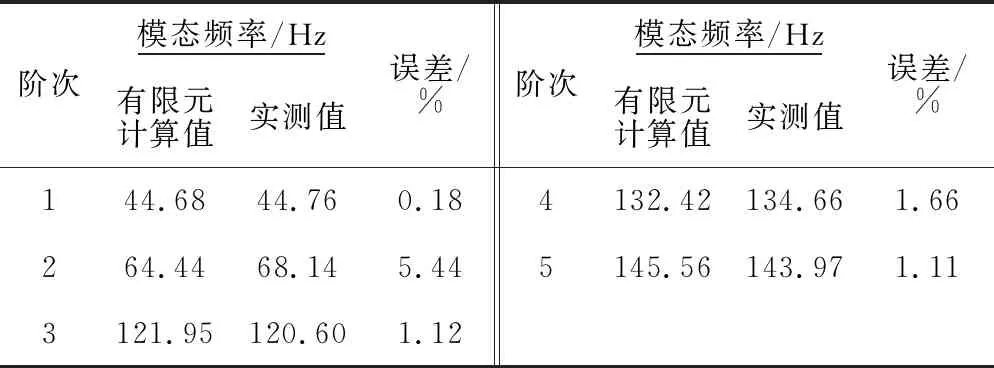
表4 实测模态频率与有限元模态分析频率对比

由表4及图10可知：缩尺箱梁的模态频率实测值与有限元计算值吻合较好，其误差多在2%以内，仅第2阶为5.44%，但模态振型相同。从整体分析，缩尺箱梁的设计制作正确，可用于箱梁振动传递试验研究。

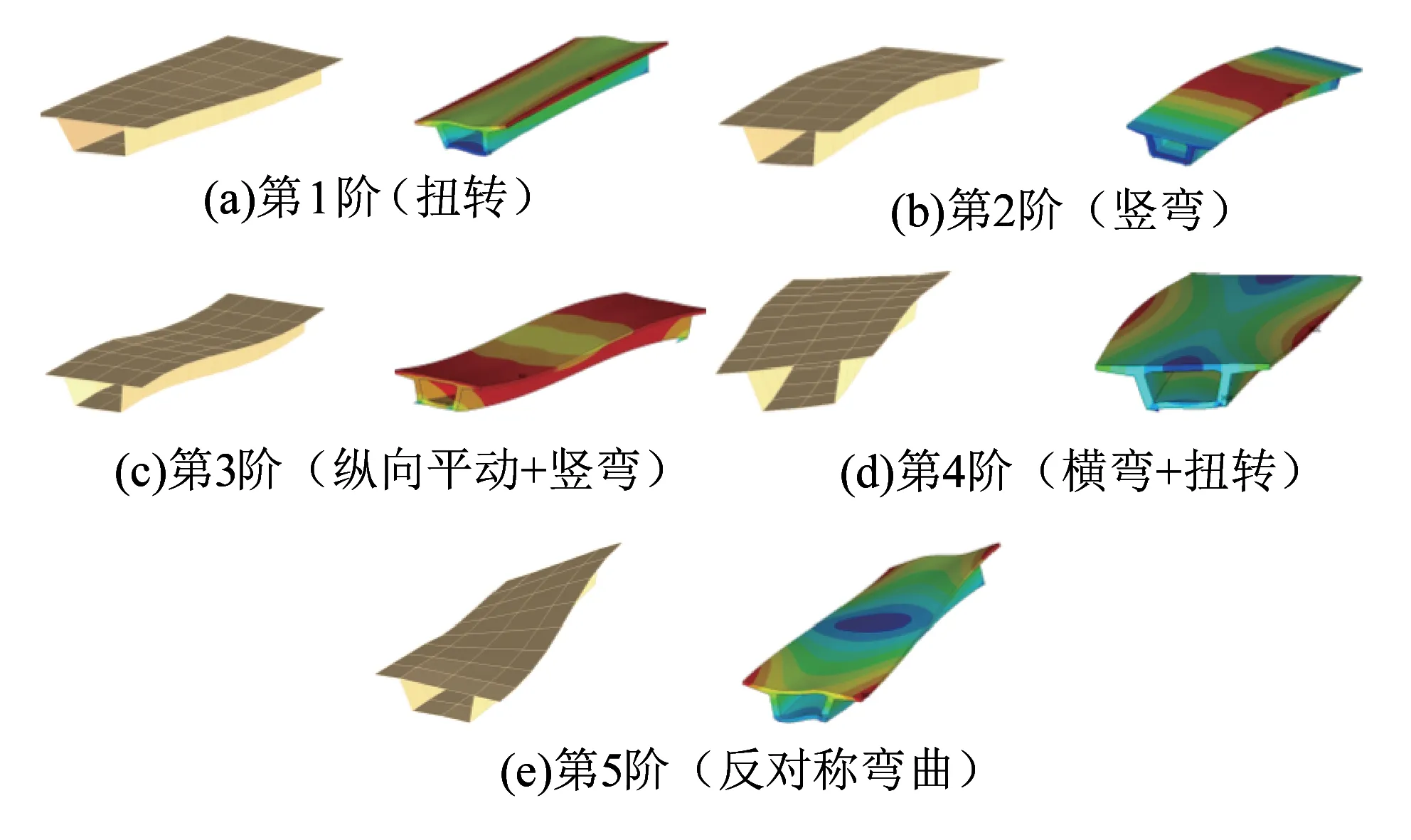
图10 模态振型对比

4 箱梁振动传递特性试验

4.1 试验原理

导纳是研究结构振动传递的重要指标，是指结构受到简谐激励时任意一点产生的响应与激励点之间幅值的比值。导纳包括位移导纳、速度导纳和加速度导纳等。研究表明，导纳仅与结构自身的固有特性有关，与输入的激励大小无关。由于锤击相比于激振器激励，便于安装且测试速度快，以及激振时对结构的附加荷载小，因此本文采用锤击法对箱梁模型系统进行导纳测试，研究振动在箱梁梁体的传递衰减规律。锤击1次即对研究范围内所有频率进行了一次试验，相当于扫频[14]。锤击试验中，箱梁各点加速度导纳HaF(ω)值为

(16)

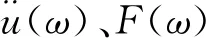
锤击试验设备除包括LMS振动数据采集与分析系统等外，还包括力锤。

根据原型箱梁与缩尺箱梁之间的频率相似比λf=0.100 664，本文锤击试验结果将直接反演至原型箱梁结构上。如需要研究原型箱梁0～200 Hz的振动传递衰减规律，则缩尺箱梁需分析0～1 987 Hz的加速度导纳。为保证力锤能够激起该频率范围内的振动，锤击点置于跨中断面的顶板中心位置，并且力锤选用钢头。图11为锤击力的功率谱密度(PSD)曲线，该结果表明在0～2 000 Hz频段内已激起较大振动，锤击效果较好。

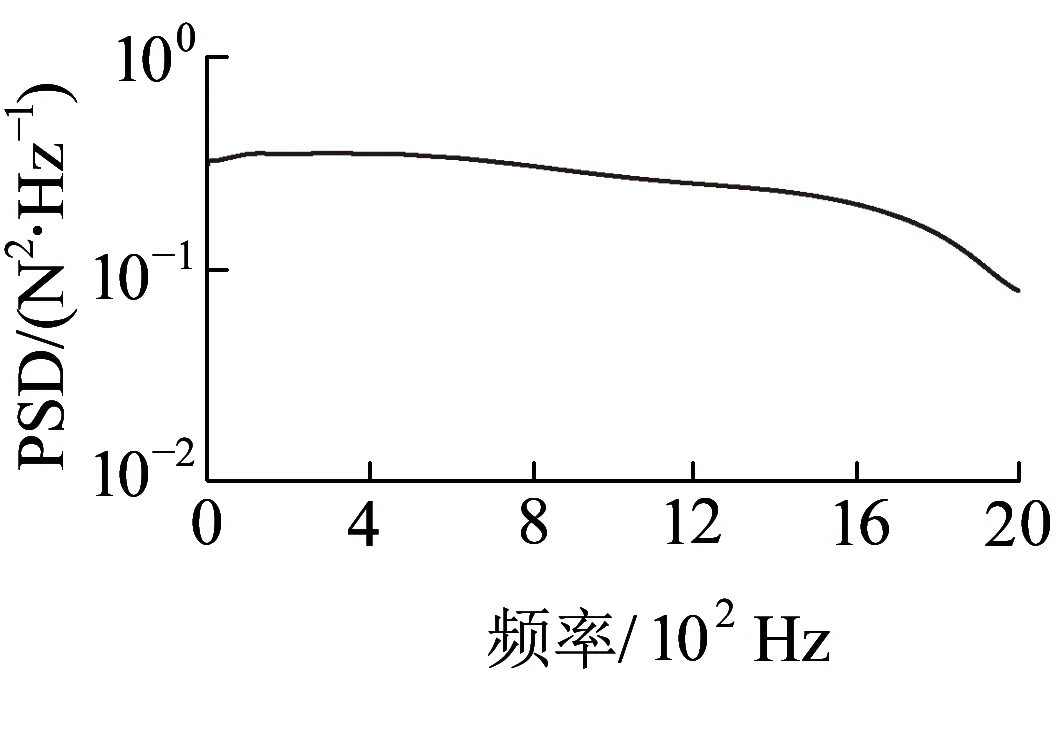
图11 锤击力的PSD曲线

4.2 各板件间的振动传递

在箱梁跨中截面上选择4个观测点，分别是观测点1(顶板中心)、观测点2(翼板边缘)、观测点3(腹板中间)及观测点4(底板中心)。锤击点位于顶板中心，见图12。支座采用支座A，图13为各观测点加速度导纳曲线对比图。

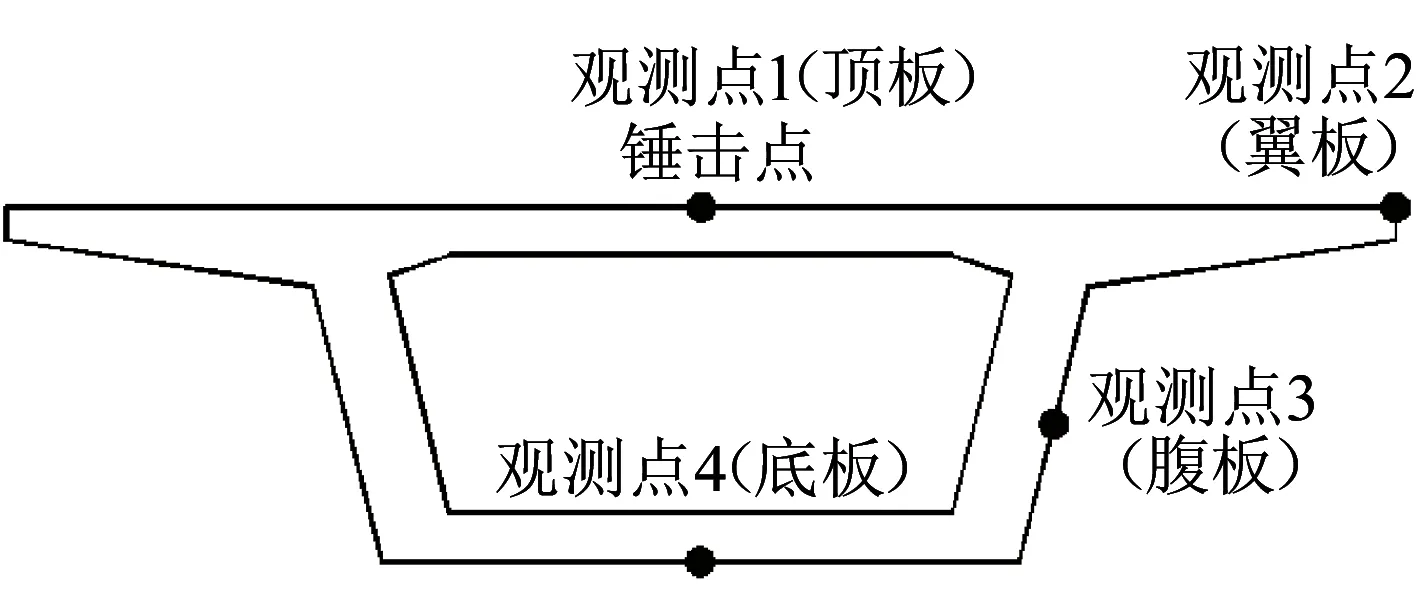
图12 观测点布置

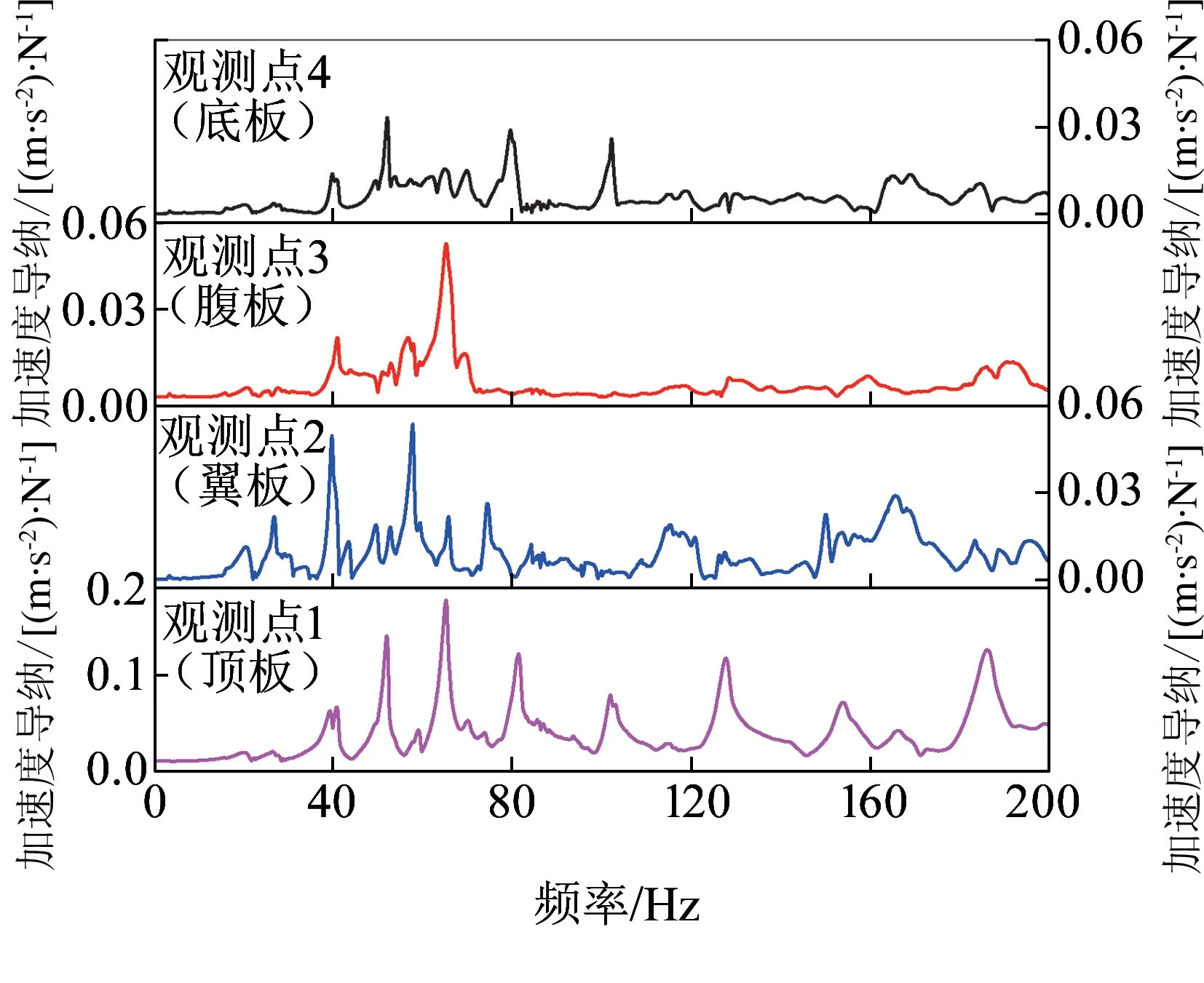
图13 各观测点加速度导纳曲线对比

由图13可知：(1)在4个观测点中，由于箱梁顶板上的观测点1(顶板)距离锤击点最近，因此其加速度导纳值最大，振动衰减最少；(2)观测点2(翼板)、观测点3(腹板)和观测点4(底板)的加速度导纳值从大到小依次是：翼板、腹板、底板，说明振动由顶板传递至翼板时，衰减速度最慢，随后是腹板，而振动由顶板传递至底板中衰减最快；(3)观测点3(腹板)在70～200 Hz时，其加速度导纳值较小，而观测点4(底板)的加速度导纳在104～200 Hz时，变化亦不大且幅值较小，表明振动在顶板到底板的传递过程中，0～200 Hz的中高频段衰减更快。

4.3 振动纵向传递特性

为进一步研究振动沿箱梁纵向传递规律，同样利用锤击试验方法，选择箱梁顶板中心线与跨中断面、1/4断面和支座断面相交的3个点作为观测点，实测锤击作用下的不同测点加速度导纳，结果见图14。

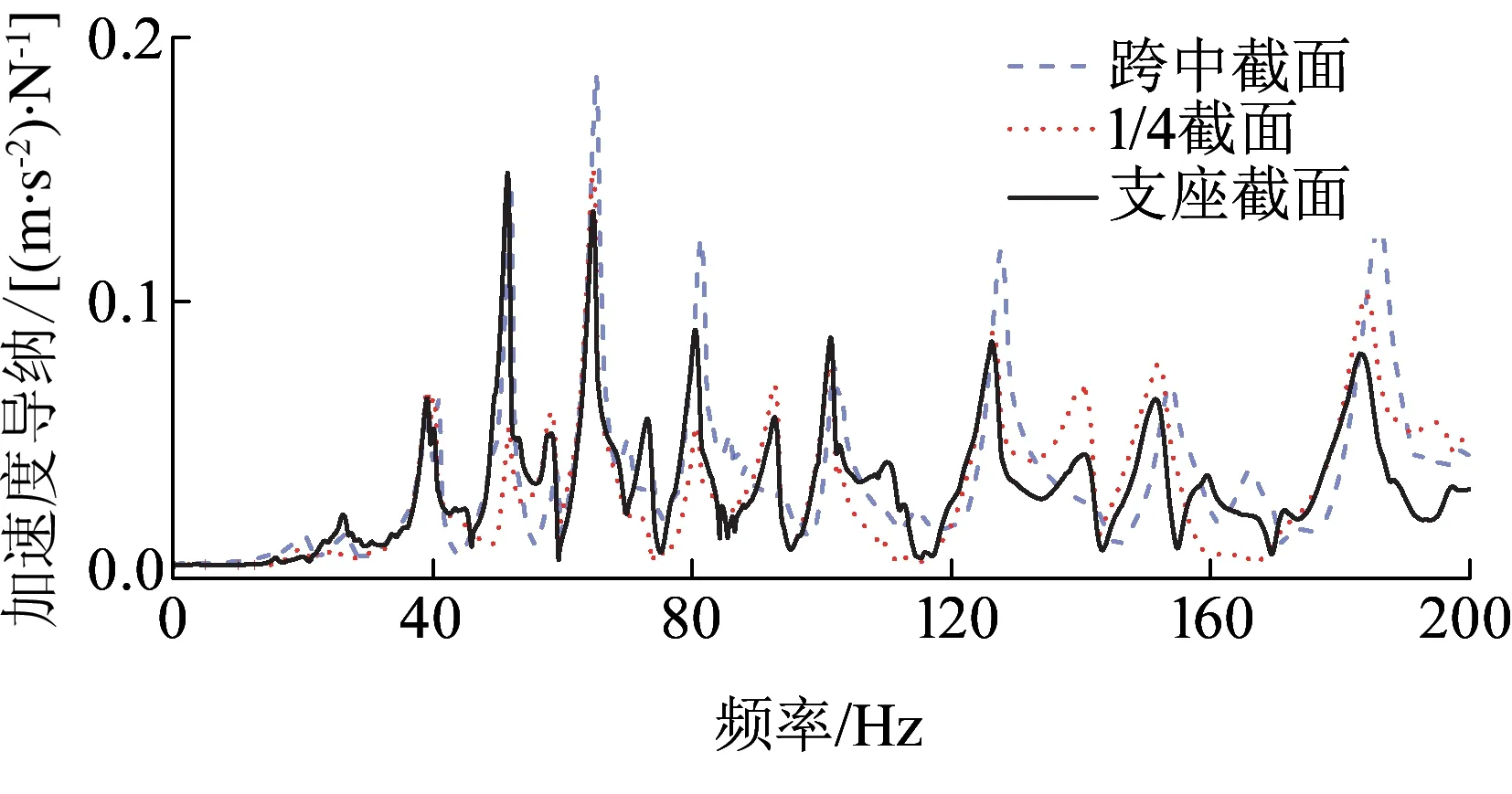
图14 各截面顶板观测点加速度导纳曲线

从图14可以看出：(1)在0～20 Hz频率范围内，各点的加速度导纳值较小，振动较弱；(2)在20～45 Hz频率范围内，各点加速度导纳值较为接近，振动由跨中向两侧的衰减速度较慢；(3)在45～200 Hz范围内，各点加速度导纳值逐渐拉开距离，除个别频率外的大多数振动得到了衰减，并且跨中截面至1/4截面之间衰减速度相对更快；(4)由跨中向支座截面传递时，f=52 Hz和f=81 Hz下的振动呈现先减小后增大的规律。其主要原因是52 Hz和81 Hz分别接近箱梁第23阶和第28阶模态频率，模态振型亦显示了该现象，见图15。

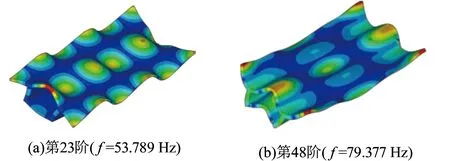
图15 模态振型

4.4 支座刚度的影响

选择缩尺箱梁跨中截面作为分析截面，以加速度导纳为评价指标，试验研究不同支座刚度(刚性支座、支座A、支座B和支座C)对跨中截面顶板、翼板、腹板和底板各观测点振动的影响。将不同支座刚度下各观测点加速度导纳数据绘成云图，结果见图16。

从图16可以看出：在相同频率位置图形形状与颜色相近，表明支座刚度对振动衰减的影响不大。

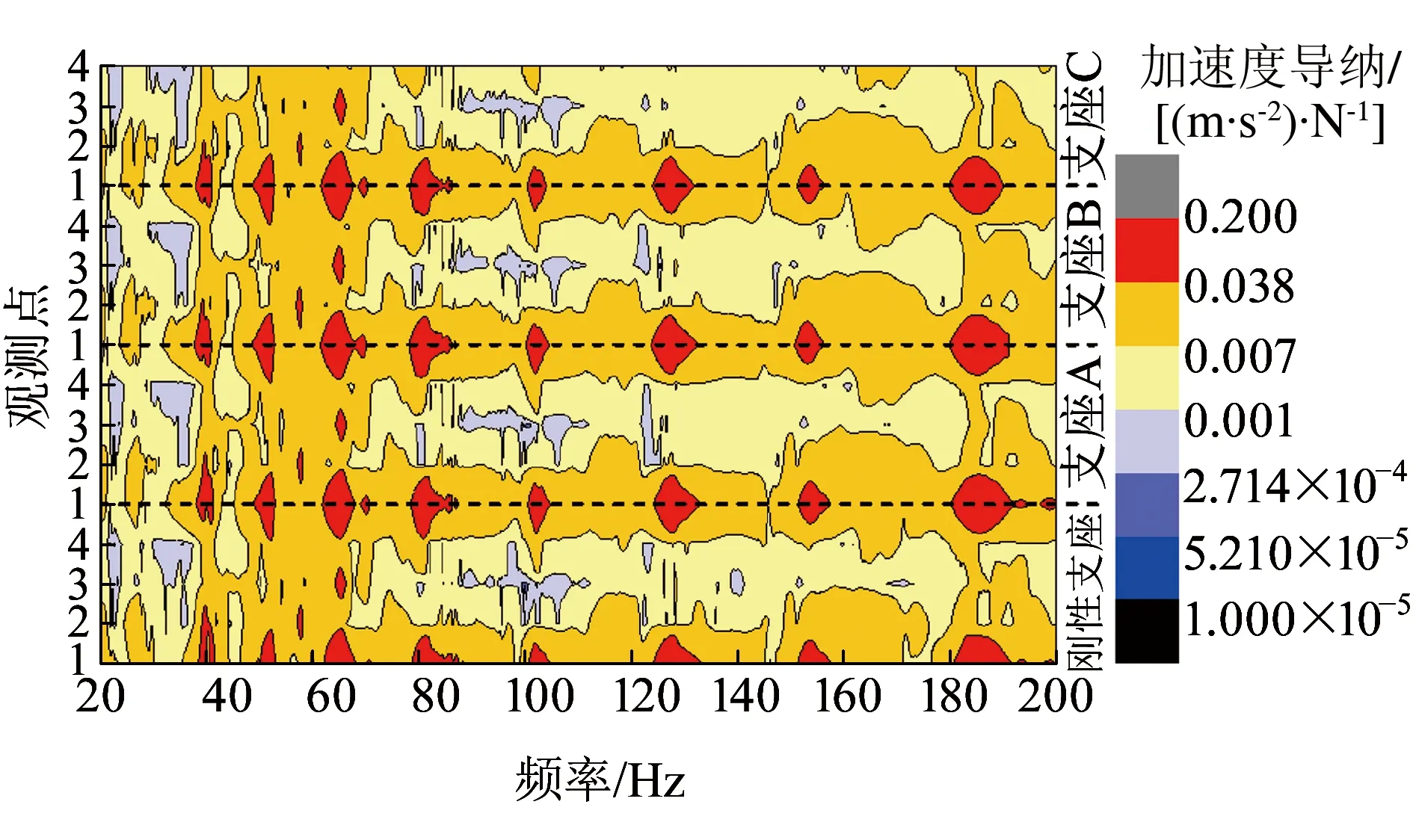
图16 各观测点加速度导纳云图

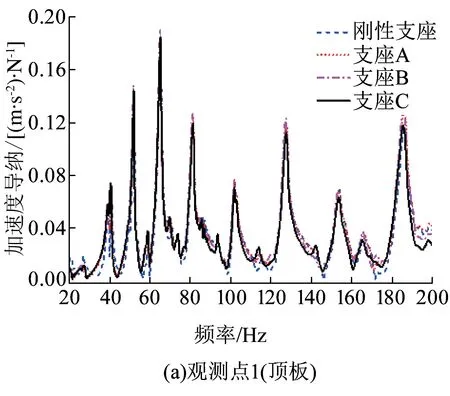
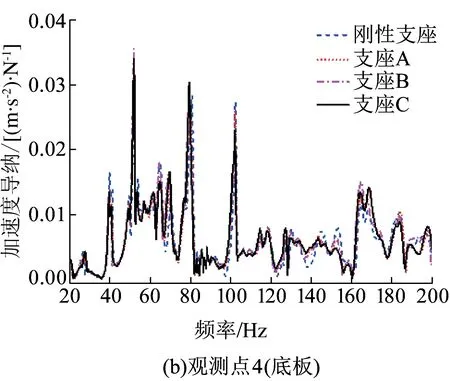
图17 各观测点加速度导纳曲线对比

为进一步了解支座刚度对某一观测点的振动影响，选取观测点1(顶板)和观测点4(底板)的加速度导纳值进行分析，结果见图17。由图17中可看出：(1)在20～110 Hz的频率范围内，各观测点在不同支座刚度下的加速度导纳曲线基本重合，表明在该频率范围内，支座刚度变化对箱梁跨中断面的振动衰减影响非常小；(2)在110～200 Hz的频率范围内，各观测点的导纳曲线出现差异，但偏差较小，表明该频率范围内，支座刚度变化会对箱梁结构振动衰减带来一定影响，但影响力有限。