基于自适应频率窗经验小波变换的列车轮对轴承多故障诊断
2019-07-12邓飞跃刘鹏飞陈恩利段修生
邓飞跃, 刘鹏飞, 陈恩利, 段修生
(1. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;2. 石家庄铁道大学 机械工程学院,河北 石家庄 050043)
轮对轴承是列车走形部中关键部件之一,长期处于高速重载的运行环境中,不仅要承受多种交变载荷影响,还要受轨道不平顺、轮对损伤等外部复杂激励的作用。因此轮对轴承极易产生裂损、剥落、麻点等各类故障,而且故障形式常常呈现并发性、复合型的特点[1-2]。轮对轴承多故障特征之间存在着较强的耦合与调制现象,加上列车运行过程中强背景噪声的干扰,使得准确分离复合故障、识别单一故障特征难度较大。
常见的共振解调、时频分析[3]、形态滤波[4]等方法主要用于轴承单一故障诊断,针对复合故障的诊断并不理想。基于此,专家们提出了多种方法用于轴承复合故障诊断:一类以多分量信号分析为主,主要基于盲源分离(BSS)与独立分量分析(ICA)技术。文献[5]利用匹配追踪算法得到多个重构信号,通过FastICA分离轴承复合故障特征;文献[6]通过双树复小波分解得到多个子信号,利用ICA分离识别复合故障特征;文献[7]研究了基于JADE算法的ICA方法,并用于多源声发射信号下复合故障特征的判离。此类方法需要分析多通道信号,实现过程较为困难。另一类以单通道信号分析为主,通过分离提取单一故障特征实现复合故障诊断。文献[8]通过正交小波分解单通道信号,利用频谱自相关抑制子信号中的弱故障特征,实现了轴承复合故障分离;文献[9]采用改进谐波小波包方法处理信号,依据不同类型故障特征权重比重构单一故障信号;文献[10]基于最小熵解卷积增强复合故障冲击特征,再结合Teager能量算子提取单一故障特征。此类方法故障诊断效果较好,对于列车轮对轴承多故障诊断具有积极的借鉴意义。
经验小波变换(Empirical Wavelet Transform, EWT)是Gilles[11]提出的自适应信号分解新方法。Kedadouche[12]研究证实:相比EMD、EEMD等方法,EWT方法计算量更小,能更有效避免模态混叠、虚假模态现象。但是EWT方法是基于信号频域极值点来分割信号频谱,存在易受强背景噪声干扰,无法准确划分频谱区间的缺陷[13]。 基于此,本文提出了频率窗EWT方法,以包络谱相关峭度ESCK为标准,通过水循环算法(Water Cycle Algorithm, WCA)优化自适应分离提取出单一故障特征,实现轮对轴承多故障自动诊断。
1 频率窗EWT方法
1.1 EWT
EWT基于信号Fourier谱分割构建小波滤波器组,通过对频谱分割区间进行正交经验小波变换提取具有紧支频谱的调幅-调频(Amplitude modulation-Frequency Modulation, AM-FM)分量。设定信号x(t)由N个AM-FM单分量成分组成,频谱范围规划为[0,π]。为了将单分量成分全部提取出来,需把[0,π]分割为N个连续区间。除去频谱自身边界点0和π外,仍需确定N-1个边界点。
信号x(t)频谱中N个连续区间表示为Λn=[wn-1,wn](n=1,2,…,N),分割频谱情况见图1,图中2τn代表频谱各分割区间的过度频带宽度。从图1中可知,以wn为中心的各个分割区间整体满足
(1)
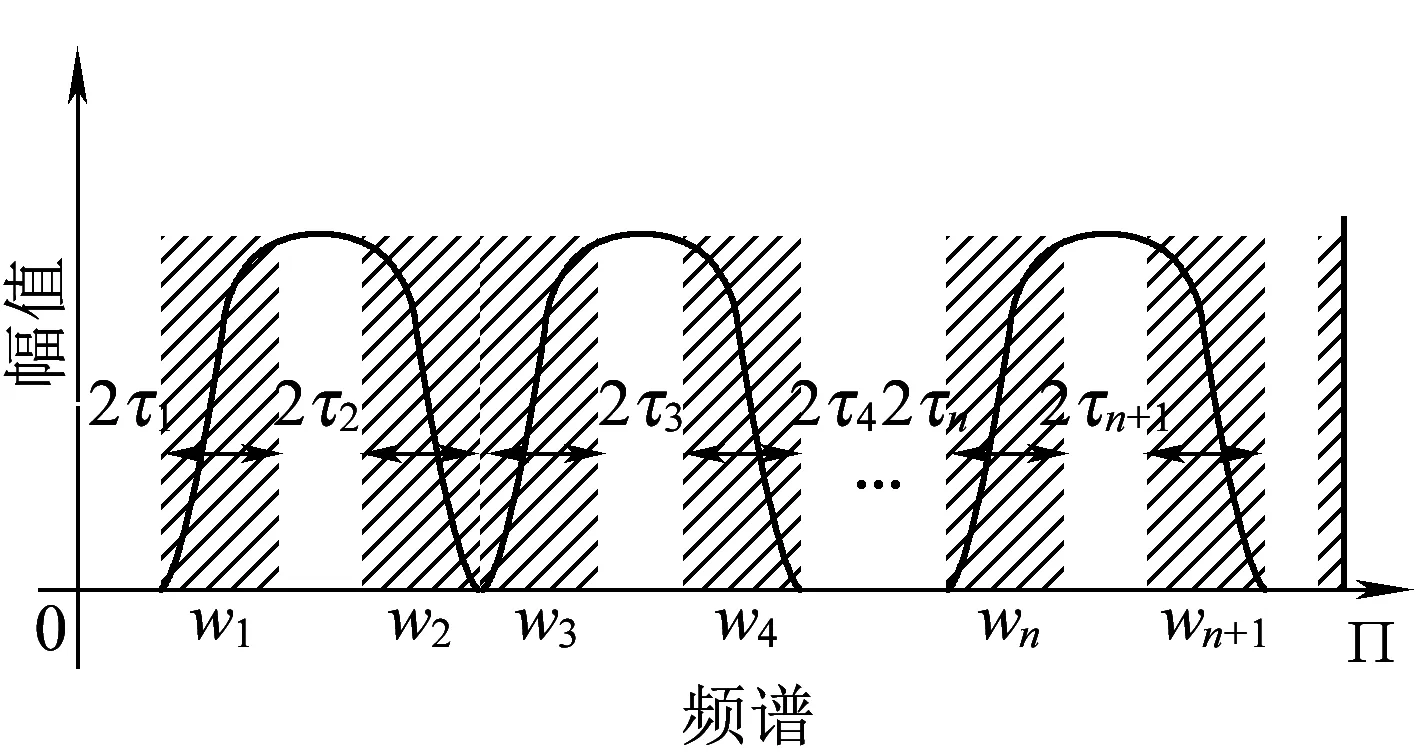
图1 信号频谱的分割
目前,常用的频谱分割方式为:一是以频谱相邻极大值之间的中间点为分割边界的“locmax”方式;二是以频谱相邻极大值之间最小值点为分割边界的“locmaxmin”方式[11]。
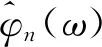
(2)
(3)
式中:ω为频率。相关参数满足如下条件
(4)
(5)
(6)
据此原信号可以重构为
(7)
xk(t)可以重新定义为
(8)
最终,信号x(t)分解为N个单分量信号之和
(9)
1.2 频率窗EWT
传统EWT方法中信号频域中极值点的分布情况直接决定了信号频谱的分割结果,如果存在强背景噪声造成的频率极值点,会严重干扰频谱的正常分割过程,进而影响提取单分量信号的准确性。针对上述不足,本文提出了频率窗EWT方法,不再以频率极值点作为频谱分割的依据,通过引入一个位置可变、带宽可变的频率窗来划分信号频谱,克服强背景噪声的干扰,直接选择信号频谱中感兴趣的频带范围进行分析。频率窗函数表示为Λ=[wa,wb],wa、wb为窗口上下频带的中心频率。频率窗可在信号全频带范围内自由滑动,带宽范围可调,分割信号频谱过程见图2,2τ为频率窗过度频带宽度。
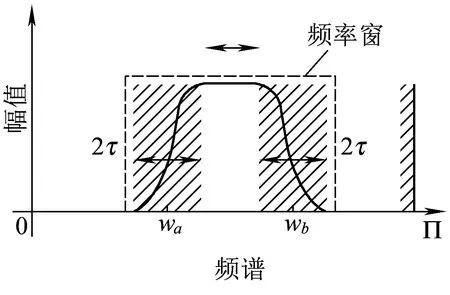
图2 基于频率窗的信号频谱分割
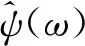
(10)
其中,相关参数需要满足如下条件
(11)
(12)
单分量信号可重构为
(13)
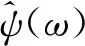
频率窗EWT方法在信号频谱区间划分上不再以频域极值点为依据,使得信号频谱分割更为灵活,可以选取感兴趣的频带范围进行分割提取,有效消除了背景噪声的干扰。
2 自适应单一故障特征提取
2.1 包络谱相关峭度(ESCK)
对于频率窗EWT分解得到的单分量信号s(t),其Hilbert变换为h(t),幅值包络a(t)为
(14)
对单分量信号幅值包络进行Fourier变换,通过频谱解调分析,可有效识别该分量信号中蕴含的特征频率信息。
峭度指标可以表征故障信号中冲击成分的强弱,冲击越强,峭度越大。以此为基础的相关峭度CK指标不仅保留了峭度特性,还具备了相关函数的特性,能有效表征信号中特定周期故障冲击成分的大小[14]。相关峭度的计算式为
(15)
式中:yi是信号序列;T为感兴趣的冲击成分周期;M为偏移的周期个数。信号中特定周期的故障冲击成分比重越多,相应的相关峭度值也越大。基于此,本文将幅值包络谱与相关峭度相结合,提出了评价信号中不同类型故障特征大小的幅值包络谱相关峭度ESCK指标。通过计算不同类型故障频率对应的ESCK值,可以评估信号中不同类型故障特征频率及倍频成分的强弱。
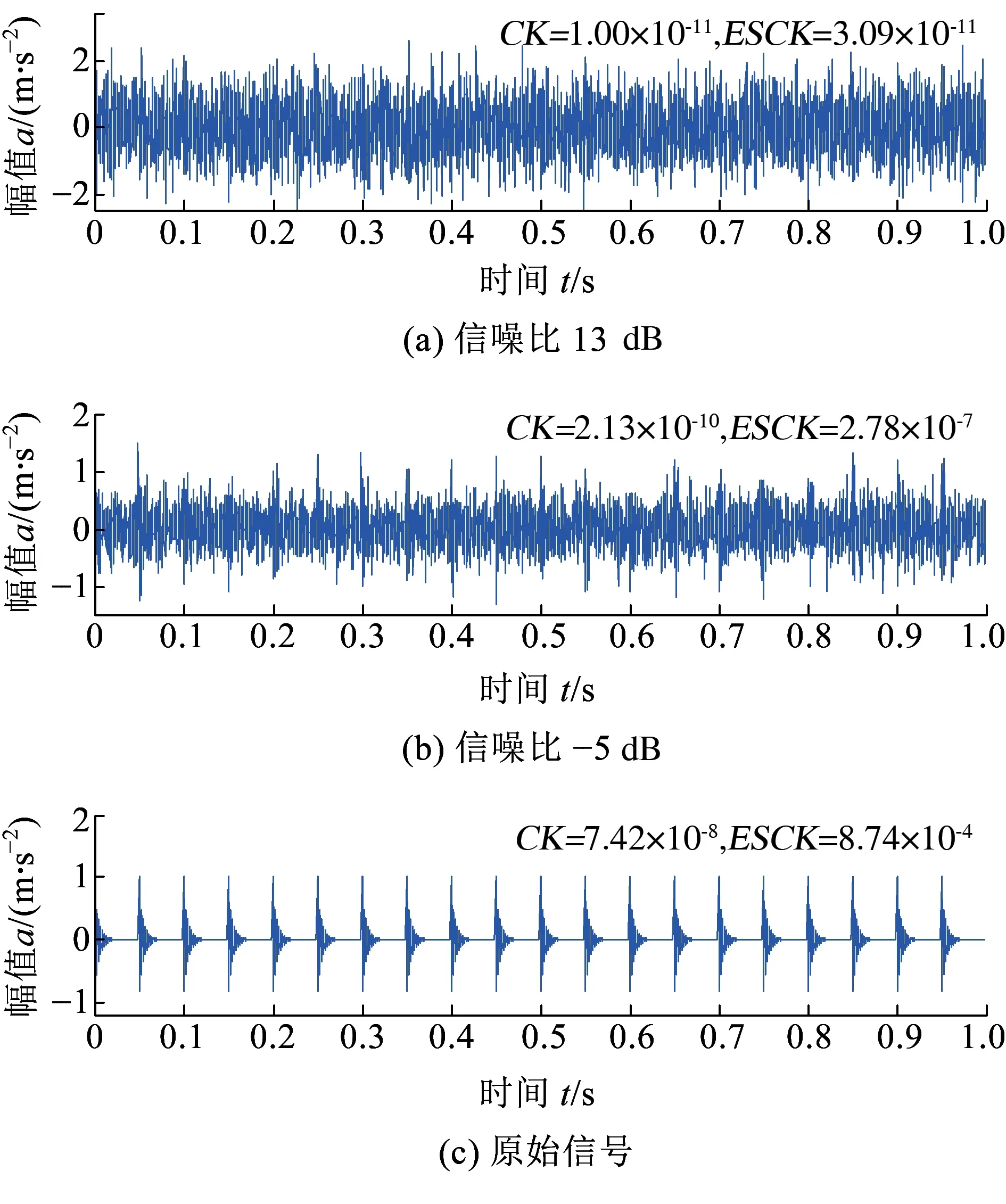
图3 不同故障程度信号的CK和ESCK比较
故障冲击仿真信号与添加不同信噪比白噪声后的结果见图3,分别计算各个信号的CK和ESCK。结果显示随着噪声干扰强度减弱,CK和ESCK数值都在增大,但ESCK增加幅度更为明显。相比CK指标,采用ESCK可以更为有效地辨识出特定周期故障冲击特征更强的单分量信号。
2.2 水循环(WCA)自适应优化
轴承元件表面发生多个故障时,传感器拾取的单通道信号是由多个单一故障源信号构成的,根据Hong等[15]提出的轴承复合故障模型,单通道轴承复合故障信号为
(16)
式中:si(t)表示第i个故障源信号;pi为si(t)的权重系数。通过不同的频率窗EWT方法可以分解得到多个AM-FM单分量信号,计算比较各个信号的ESCK值,可以找出特定周期故障特征最强的单分量信号。
WCA方法是Eskandar等[16]提出的一种新的嵌入启发式优化算法,通过模拟现实环境中水的自然循环过程来实现目标最优化选取,具有运算效率高,不易陷入局部最优解“陷阱”等优点。本文以ESCK为适应度函数,应用WCA优化自适应确定各单一故障信号最优的频率窗位置,自动实现轴承复合故障的诊断。算法流程见图4。
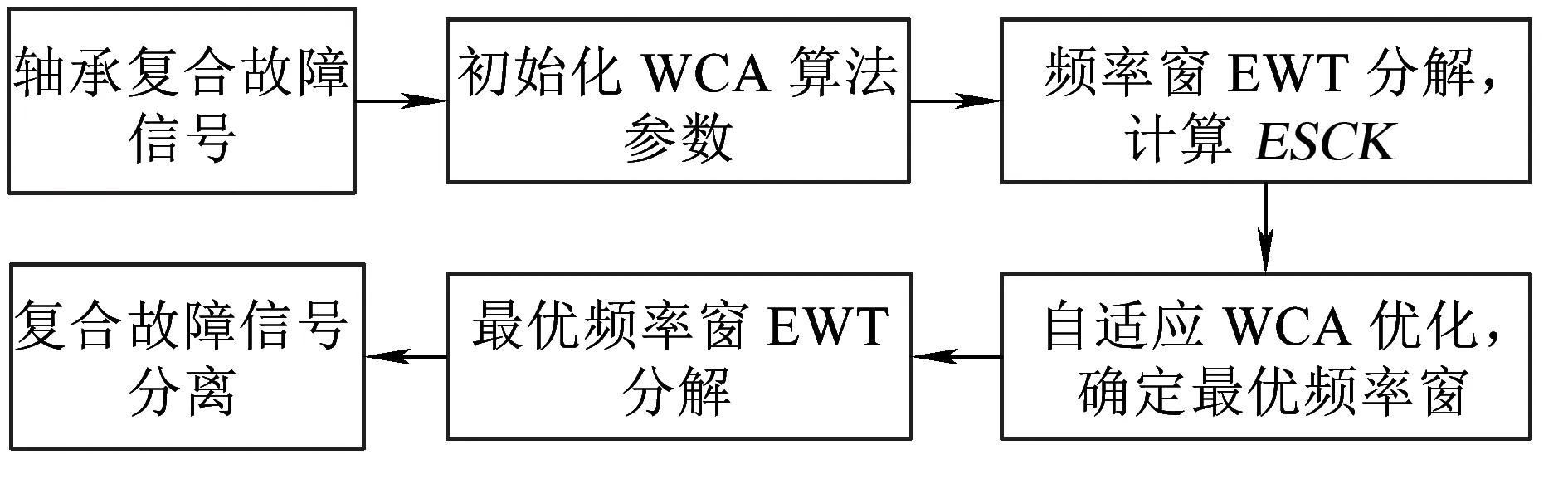
图4 算法流程
具体实现过程如下:
(1) 初始化WCA算法各项参数并设定频率窗上下截止频率wa和wb的约束条件。其中:规模总数Npop=50,江河和海洋总数Nsr=2,蒸发条件常数dmax=1×10-5,最大迭代数MI=100。
(2) 对轴承复合故障信号基于不同的频率窗进行EWT分解,计算各个单分量信号的ESCK作为下降度,计算水循环过程中溪流到江河、江河到海洋的多个下降度数值,获取最大ESCK值为最优下降度。
(3) 判断是否满足蒸发条件,如果满足,开始蒸发降雨过程,再次寻找水循环过程中最优下降度,直至不再满足蒸发条件。
(4) 通过迭代运算,不断更新溪流、江河和海洋位置,在满足优化算法收敛准则的基础上,结束水循环过程,输出最优频率窗的wa和wb。
(5) 对轴承复合故障信号进行最优频率窗EWT分解,分解出单一故障信号并进行包络解调分析,分解轴承复合故障信号。
3 轮对轴承复合故障仿真信号分析
根据列车轮对轴承故障类型及故障信号特征,仿真轮对轴承复合故障信号,对本文所提方法进行验证。当外圈发生损伤故障时,由于轮对轴承安装在列车轮对轴箱内,轴承外圈故障信号主要表现为冲击调制现象,受系统阻尼影响,故障冲击成分呈指数衰减形式。当内圈发生损伤故障时,由于轴承内圈随列车轮对旋转,并受滚动体在内圈表面转动的影响,内圈故障信号主要表现为复杂的调制现象,其主要为内圈故障冲击与车轴旋转、滚动体公转之间的振幅调制。当滚动体发生故障时,由于滚动体存在公转与自转,滚动体故障信号主要表现为滚动体故障冲击与滚动体公转之间产生的振幅调制,并伴有滚动体相对于滚道的轻微随机滑动。
基于上述分析,列车轮对轴承内、外圈及滚动体复合故障仿真信号x(t)为
(17)
x(t)=x1(t)+x2(t)+x3(t)+r(t)
(18)
式中:h(t)为单个故障周期冲击信号;x1(t)、x2(t)、x3(t)分别为外圈、内圈和滚动体故障仿真信号;r(t)为添加的背景噪声,此处添加信噪比为-8 dB的高斯白噪声;ζ为阻尼系数;Ai为第i次谐波分量的振动幅值;θ、θ1、θ2分别为各谐波信号的初始相位;τi为标准差为转速0.5%的随机滑动,服从正态分布。设定轮对转频fr=13 Hz,外圈、内圈和滚动体故障频率分别为fo=80 Hz、fi=65 Hz、fb=45 Hz,采样频率fs=10 000 Hz。
轮对轴承单一外圈、内圈和滚动体故障仿真信号见图5,各单一故障信号及噪声叠加后,轴承复合故障信号及其包络谱见图6。从包络谱中虽然可以提取出轴承外圈、内圈及滚动体故障特征频率,但彼此混杂在一起,而且内圈故障特征频率相对微弱,极易被忽视造成误诊,因此无法准确诊断轴承的复合故障。
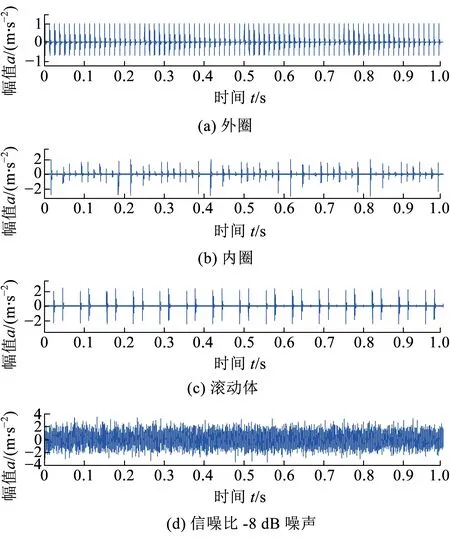
图5 轮对轴承仿真故障信号

图6 轮对轴承复合故障仿真信号
利用本文所提方法,设置频率窗带宽约束条件为
wb-wa≥3fo=240 Hz
(19)
利用WCA优化自适应确定轴承不同类型故障对应的最优频率窗位置,然后分别进行最优频率窗EWT分解,分解后轴承各单一故障信号见图7。图7中轴承各单一类型故障信号所对应的包络谱中清晰地提取了外圈、内圈、滚动体故障特征频率及倍频成分,不仅实现了不同类型复合故障特征分离,而且准确提取了轴承各单一故障特征信息,通过仿真信号分析,证实了本文所提方法的有效性。
4 实例分析
型号为352226X2-RZ型轮对轴承安装在某型号铁路货车轴箱轴承支座上,通过列车轮对跑合实验台进行振动测试实验。列车在长期运行过程中,轴承外圈和内圈表面均出现了剥落故障,见图8。实验中,轮对转速为465 r/min,采样频率为25 600 Hz。计算得到的轮对转频fr=7.75 Hz,轴承外圈和内圈故障特征频率分别为fo=66.75 Hz、fi=88.24 Hz。
传感器拾取的单通道轮对轴承复合故障信号见图9,信号波形非常复杂,包含了大量背景噪声。频谱中没有明显的故障特征信息,高幅值频率成分主要集中在0~2 000 Hz范围内。包络谱见图10,图中显示出较为清晰的内圈故障特征信息及较强的转频调制现象。但是,包络谱中没有任何外圈故障特征的信息,因此会误诊为轮对轴承仅发生了内圈故障。
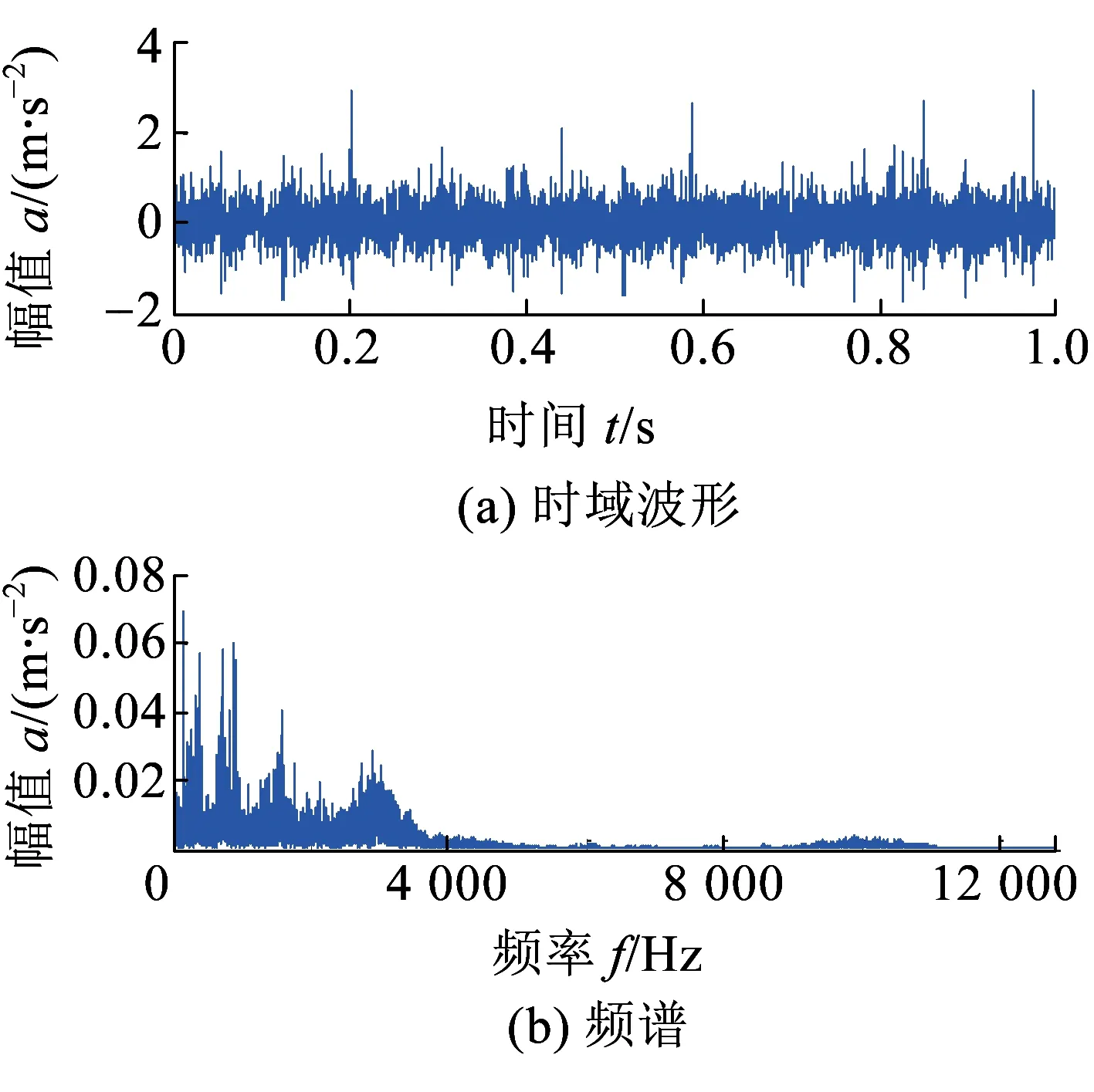
图9 测试轮对轴承复合故障信号
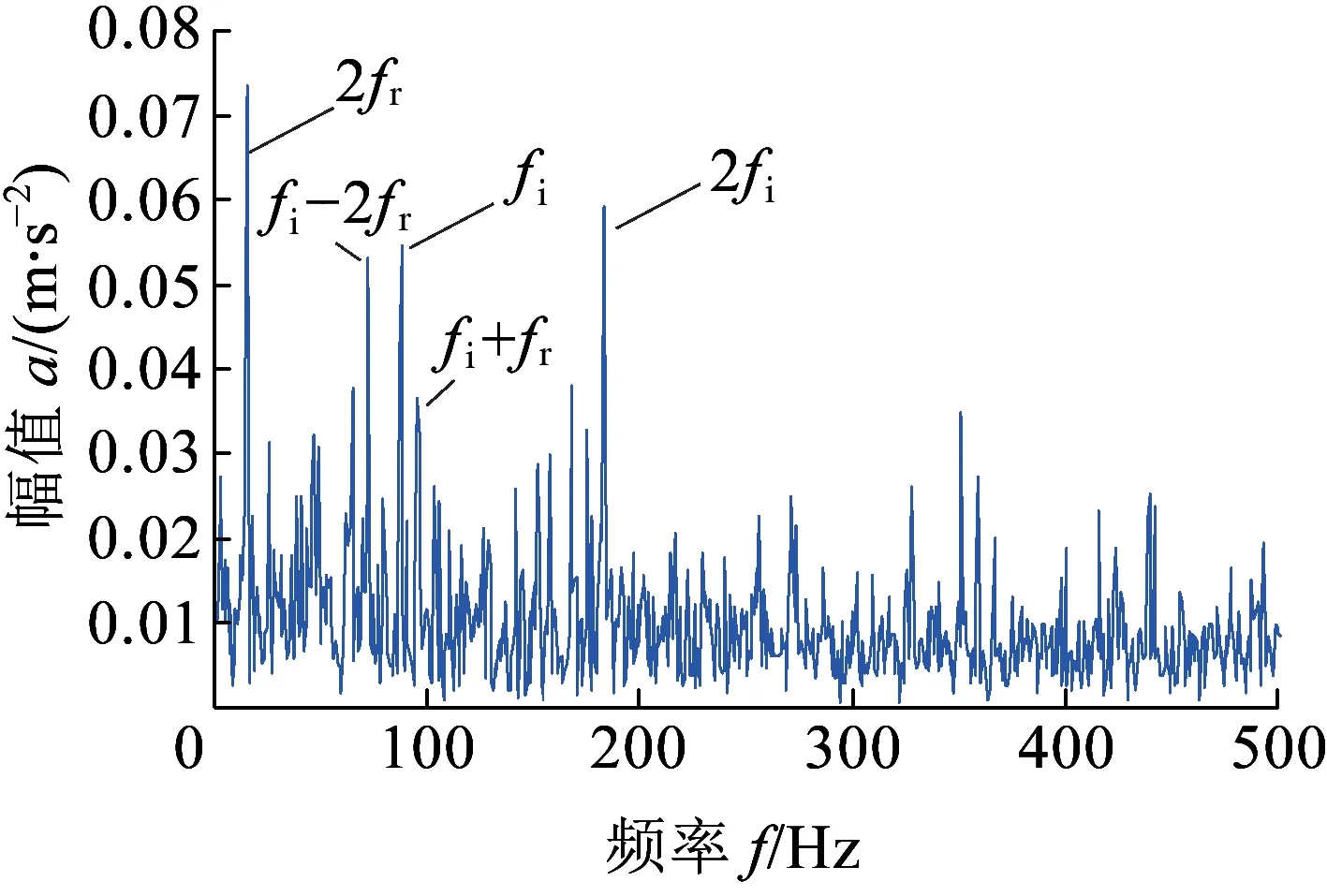
图10 测试轮对轴承复合故障信号包络谱
利用本文所提方法分析该轴承复合故障信号,先设置频率窗带宽约束条件为
wb-wa≥3fi≈265 Hz
(20)
进行WCA优化处理,自适应确定内外圈故障所对应的最优频带范围分别是3 128~4 400 Hz、7 530~7 851 Hz,在信号频谱中的位置见图11。设置频率窗位置与内外圈故障最优频带范围一致,通过EWT分别得到轮对轴承内外圈故障单分量信号,信号波形及包络谱结果分别见图12、图13。图12中,轴承内圈故障信号中周期性冲击成分十分明显,故障特征频率及倍频成分清晰,两边的边频带显示出内圈故障冲击受到了转频较强的调制作用。图13中,外圈故障冲击成分也较为明显,外圈故障频率及二倍频被有效地提取出来。诊断结果表明论文所述方法在列车轮对轴承复合故障分离及单一故障特征识别上具有良好效果。
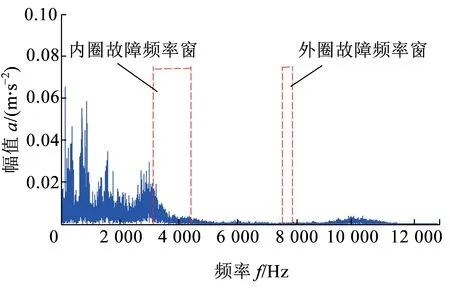
图11 内、外圈故障频率窗位置
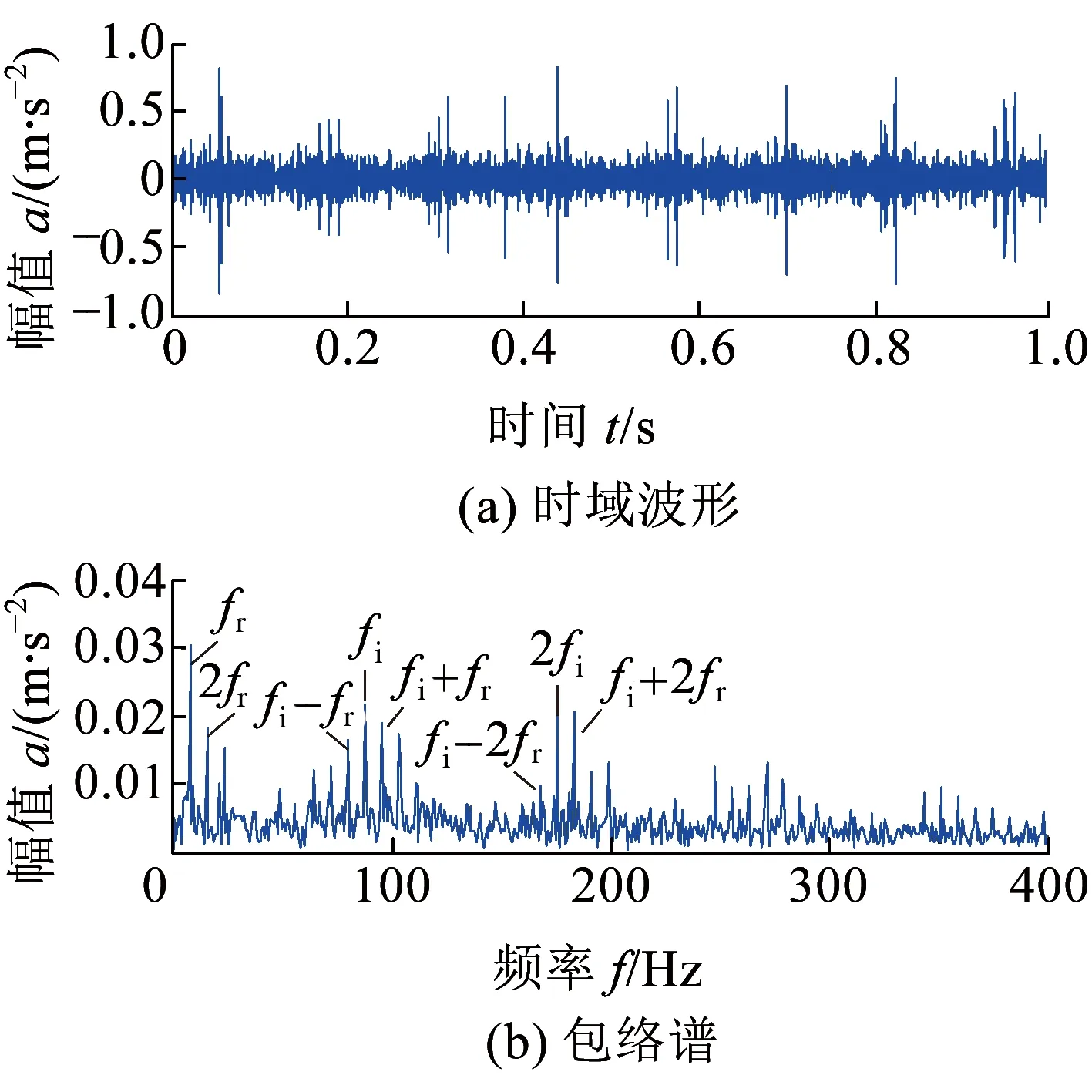
图12 分离后轴承内圈故障信号
采用文献[17]提出的传统EWT方法分解轮对轴承复合故障信号与本文方法进行比较,设定信号频谱,划分方式为“locmaxmin”,分割区间N=6,该频谱分割方式是以信号频谱中两频率极大值点间最小的频率值为频谱分割边界,得到的信号频谱分割结果见图14。由于信号中强背景噪声造成的高幅值的杂频成分主要位于低频段内,因此对信号频谱的划分也主要在该范围内,划分细节见图14(b)。分解后各个单分量信号及包络谱见图15。从图15中可知,仅分量6信号中显示出清晰的内圈故障特征,其余分量信号完全没有提取出有关轴承外圈故障特征的任何信息。通过上述对比可进一步证实本文所提方法能更加灵活地划分信号频谱,克服了传统EWT方法在分割信号频谱方面的不足。
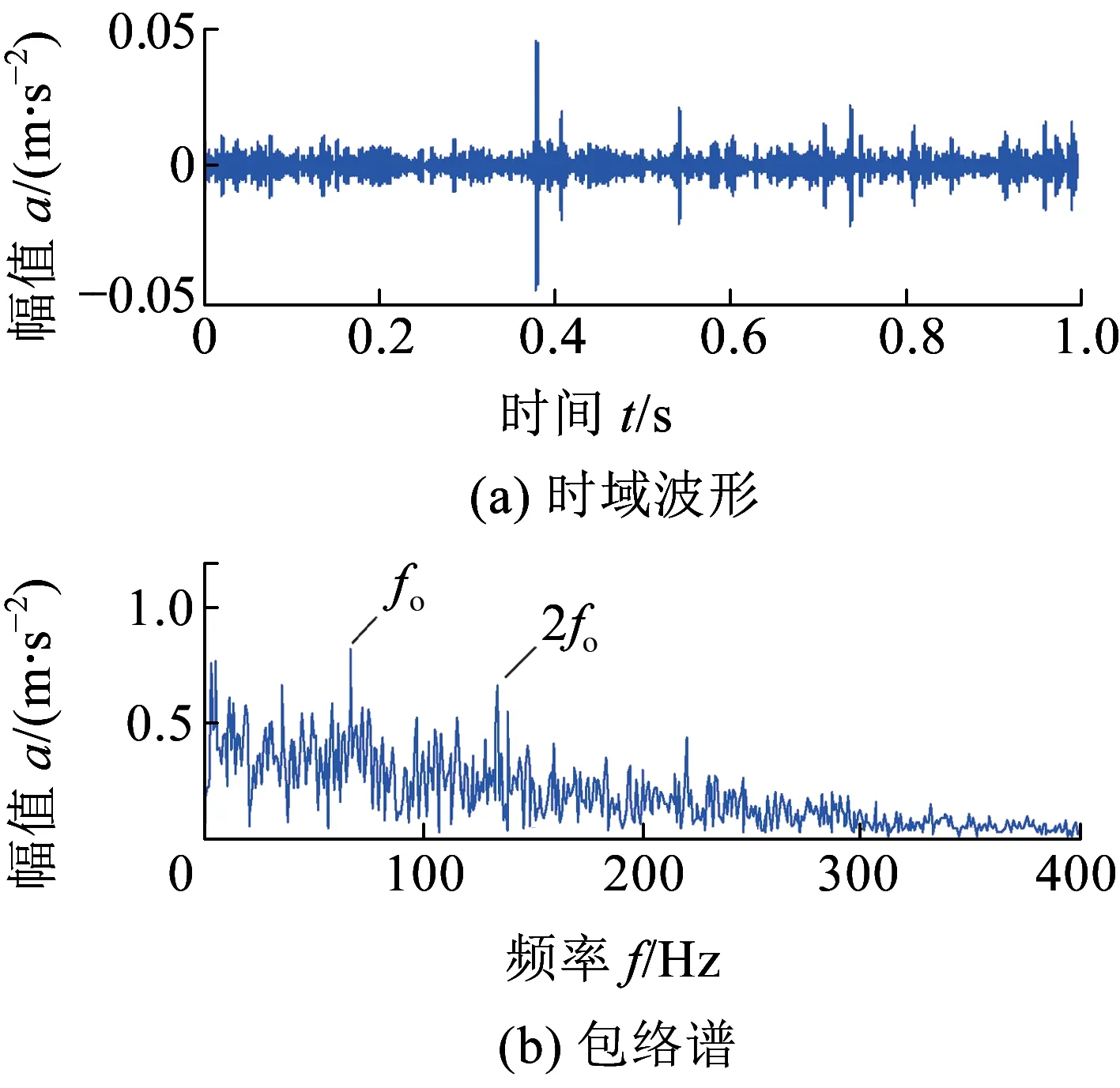
图13 分离后轴承外圈故障信号
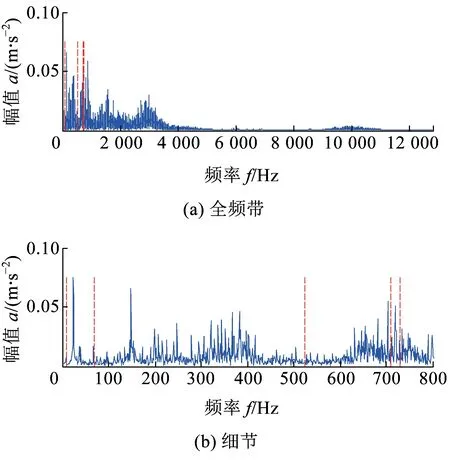
图14 EWT方法分割信号频谱
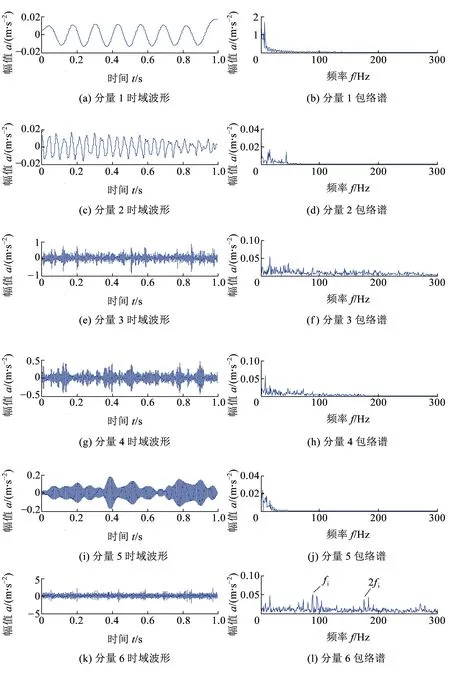
图15 EWT分解后结果
5 结论
本文提出了基于频率窗EWT的列车轮对轴承复合故障诊断方法,能够自动分离单通道复合故障信号,有效识别单一故障特征,具有一定的工程应用价值,得出相关结论如下。
(1) 频率窗EWT方法通过引入一个带宽可变的滑动频域窗,弥补了传统EWT方法基于信号频域极值点划分频谱区间的不足,有效消除了强背景噪声干扰频率的影响。
(2) 本文提出采用ESCK指标评价特定故障周期的单一故障信号,并使用WCA优化方法自适应确定最优频率窗位置,实现了轮对轴承复合故障特征分离,通过仿真和实验证实了所提方法的准确性,也为其他类型旋转机械故障诊断提供了参考。
