例析数列不等式高考题的证明破解策略
2019-07-12广东省佛山市第一中学528000吴统胜
广东省佛山市第一中学(528000) 吴统胜
2017年是全国新高考改革的元年,而数列不等式放缩是2017年浙江新高考的压轴题和每年名校自主招生必考题,究其原因在于其不仅能很好地考查学生逻辑推理能力和创新能力,而且级数不等式的处理也是高等数学特别重要的一部分,它是初等数学向高等数学跨越的基础,也体现了中学数学与高等数学间的联系与衔接.高考数学全国卷常将数列作为中档题考查,涉及数列求通项、求和及数列型不等式的证明, 好些省份还将数列型不等式的证明作为压轴题来考查.因此研究数列不等式的放缩问题显得很有必要.数列不等式放缩的核心是数列的极限思想.笔者在贵刊2018年第2 期(下半月)刊出的《数列的求通项与求和》一文中,非常详细、系统地举例说明了递推数列中求通项、求和的几种常用基本方法,对数列求和中涉及的常见放缩方法也进行了较详细的探究、归类和总结,并得到了一些易于操作的一般性的放缩策略和方法.本文笔者将结合数列不等式高考题更进一步系统地举例说明数列不等式的一般性的证明破解策略,以期对广大师生在解决此类问题时带来一定的帮助.
策略一裂项相消或放缩为裂项相消化简求和证明
例1(2013年广东理科第19 题)设数列{an}的前n 项和为Sn.已知
(I) 求a2的值;
(II) 求数列{an}的通项公式;
解析(I) a2= 4(过程略); (II) an= n2,n ∈ℕ∗(过程略);
(III) 由(II)知,an=n2,n ∈ℕ∗.

例2(2013年江西理科第17 题)正项数列{an}的前n项和Sn满足:-(n2+n-1)sn-(n2+n)=0.
(1) 求数列{an}的通项公式an;
解析(1) an= 2n (过程略); (2) 证明: 由于则
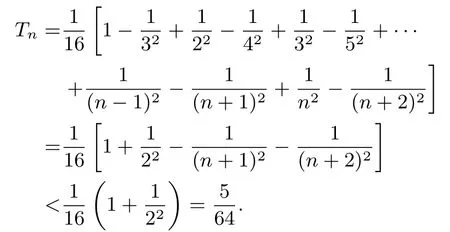
点评例1 第(III)问是先放缩再利用裂项相消法化简求和得证原不等式.例2 第(2)问直接利用裂项相消法化简求和证明.
策略二放缩为等比数列化简求和证明
例3(2012年广东理科第21 题) 设数列{an} 的前n 项和为Sn, 满足2Sn= an+1- 2n+1+ 1(n ∈ℕ∗), 且a1,a2+5,a3成等差数列.
(1) 求a1的值;
(2) 求数列{an}的通项公式;
解析(1) a1=1(过程略);(2) an=3n-2n(过程略);
(3)证法一当n = 1 时,当n ≥2时,所以3n>2 × 2n, 所以an=3n-2n>2n,所以所以

证法二因为所以

所以

点评放缩的目的是为化简求和,本例中证法一是先放缩为等比数列,再求和化简证明.证法二则是分离出非负数项进行放缩,放缩为等比数列求和化简得证原不等式,此放缩方法可操作性强,可实现精准放缩,是通性通法!一般地,形如可放缩为

可快速转化为等比数列化简求和.2013年江西第17 题也是此类题型.
该题稍作改编后便是2014年全国II 卷理科第17 题:
例4(2014年全国II 卷理科第17 题)已知数列{an}满足a1=1, an+1=3an+1.(1) 证明是等比数列, 并求{an}的通项公式;
解析(1)(过程略);
(2)证法一由(1)知所以因为当n ≥1 时,3n-1 ≥2×3n-1,所以所以

证法二因为3n-1-1 ≥31-1-1=0,所以
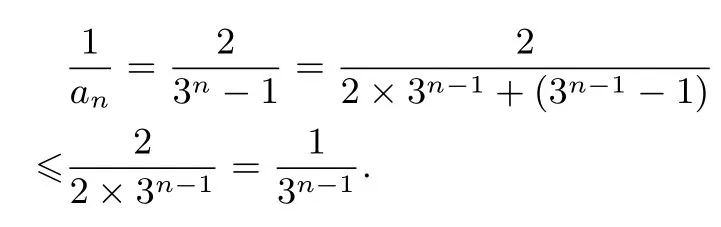
以下过程同证法一.
点评直接放缩为等比数列求和化简即可迅速得证! 但若考生没有掌握基本的放缩方法和技巧,是不可能在考试中快速解决此类数列不等式题型的,故在高考复习备考中要注意覆盖好数列不等式中基本的放缩方法和技巧.
例5(2007年四川文科第22 题)已知函数f(x)=x2-4,设曲线y = f(x)在点(xn,f(xn))处的切线与x 轴的交点为(xn+1,0)(n ∈ℕ∗),其中x1为正实数.
(I) 用xn表示xn+1;
(II) 若x1= 4,记证明数列{an}成等比数列,并求数列{xn}的通项公式;
(III) 若x1=4,bn= xn-2,Tn是数列{bn}的前n 项和,证明Tn<3.
解析(I) 由题可得f′(x)=2x.所以曲线y =f(x)在点(xn,f(xn))处的切线方程是: y-f(xn)=f′(xn)(x-xn).即令y =0,得2xn(xn+1-xn).即+4 = 2xnxn+1.显然xn0,所以



当n=1 时,显然T1=b1=2 <3.当n >1 时,所以

综上,Tn<3(n ∈ℕ∗).
点评(方法提炼)本例题采用的是放缩为等比数列求和化简证明,此放缩法可操作性强,是通性通法,应引导学生理解和熟练掌握该放缩证明的方法.但如何把握放缩的“度”,即如何找寻其中的“公比”q,从而实现精准放缩呢? 下面我们以本例题第(III)问举例说明其具体操作过程,关键在于找寻使

成立的“公比”q(0 <q <1).原不等式即证

(因为0 <q <1,所以0 <1-qn<1).令即得由此便可实现快速精准的放缩,得到该类数列不等式的程序化、套路化的证明方法.当然,具体证明过程中也要注意是从第1 项还是从第2 项或第3 项开始放缩等细节问题.读者可以尝试利用该方法快速找寻例3 第(3)问及例4第(2)问中的“公比”.
策略三放缩后利用累乘法化简证明
例6(2009年广东理科第21 题改编) 已知曲线Cn: x2-2nx+y2= 0(n = 1,2,...).从点P(-1,0)向曲线Cn引斜率为kn(kn>0)的切线ln,切点为Pn(xn,yn).
(1) 求数列{xn}的通项公式;
解析(1) 设直线ln: y = kn(x + 1), 联立x2-2nx+y2= 0 得则所以舍去),所以即
(2) 证明: 因为

又因为


策略四构造函数型不等式放缩,再求和化简证明
例7(2015年广东理科第21 题) 数列{an} 满足a1+2a2+···+nan=4-
(1) 求a3的值;
(2) 求数列{an}前n 项和Tn;
解析(1)(过程略);(2)(过程略);


点评如何构造函数放缩为函数型不等式, 进而通过赋值转化为数列不等式化简求和证明原不等式? 我们可以通过分析法, 借助数学归纳法找寻解题时需构造的函数型不等式, 其具体操作过程如下: 原不等式即

当n=k+1 时,即证

例8求证:

解析因为ln x ≤x-1(x >0),所以ln n2≤n2-1,所以
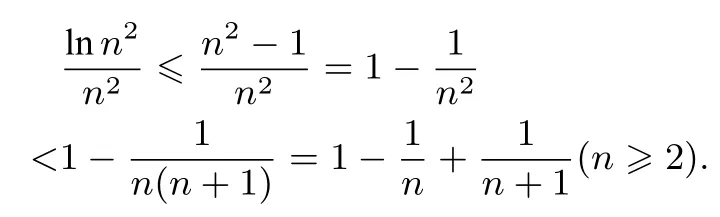
令n=2,3,...,n 各式相加得: 所以

类似题型还有2010年湖北理科第21 题:
(I) 用a 表示b,c;
(II)若f(x)≥ln x 在[1,+∞)上恒成立,求a 的取值范围;
例9已知函数f(x)=ex-x(e 为自然对数的底数).
(1) 求函数f(x)的最小值;
(2) 若n ∈ ℕ∗, 证明:
解析(1) f(x)有最小值1.
(2) 由(1) 知, 对任意实数x 均有ex- x ≥ 1, 即1 + x ≤ex.令则所以


因为

变式拓展题
求证:

例10求证:

证法一利用伯努利不等式(1 + x)n≥ 1 +nx(n ∈ℕ∗,x >-1)放缩证明(可用构造函数法或数学归纳法证明该不等式)
由伯努利不等式(1+x)n≥1+nx(n ∈ℕ∗,x >-1),


故原不等式得证!
证法二利用不等式性质放缩证明
变式拓展题(2006年重庆理科第21 题改编)求证:

点评常用于放缩的函数型不等式主要有以下三种类型:
类型1ex≥x + 1 或ln(x + 1) ≤x,(x >-1) 或((见人教版教材《选修2-2》P32 习题1.3B 组第1 题);
类型2
类型3x ≤1).
策略五利用数学归纳法证明
例11(2009年山东理科第20 题)等比数列{an}的前n 项和Sn为已知.对任意的n ∈ℕ∗, 点(n,Sn) 均在函数y =bx+r(b >0 且b1,b,r 均为常数)的图象上.
(I) 求 r 的值; (II) 当 b = 2 时, 记 bn=2(log2an+1)(n ∈ℕ∗), 证明: 对任意的n ∈ℕ∗不等式成立.
解析(1)an=(b-1)bn-1(过程略);
(2)当b=2 时,an=(b-1)bn-1=2n-1,
bn=2(log2an+1)=2(log22n-1+1)=2n,
证法一下面用数学归纳法证明不等式

成立.
②假设当n=k 时不等式成立,即

成立.则当n=k+1 时,

所以当n=k+1 时,不等式也成立.
由①、②可得不等式恒成立.
证法二利用策略三,放缩后利用累乘法化简证明
因为


证法三利用基本不等式0)放缩证明
策略六利用并项放缩求和化简证明
例12已知数列{an} 满足a1= 1,an+1= 2an+(-1)n+1.
(1)求数列{an}的通项公式;
解析(过程略);
(2) 因为

当n=2m-1(m ≥1)时,有

当n=2m(m ≥1)时,有

