不畏浮云遮望眼 只因“背景”在心中—探究一道圆锥曲线小题的命制背景

广东省广州大学附属中学(510006) 陈经纬

关键字 背景;蒙日圆;切线

数学教学离不开解题教学，通过解题教学能使学生加深对概念的理解和方法的运用，促进思维能力的提升.在解题教学中，教师仅仅展示解题过程和结果是不够的，要深刻地分析试题的命制背景，只有把“背景”讲透了，才能让学生居高临下看问题，实现解题能力实质性的突破，本文以一道圆锥曲线小题为例，探究试题的命制背景.

一、问题的提出

题目如图1， 椭圆圆O : x2+ y2= a2+ 4， 椭圆C 的左、右焦点分别为F1，F2，过椭圆上一点P 和原点O 作直线l 交圆O 于M,N 两点，若|PF1|·|PF2|=6，则|PM|·|PN|的值为____.

图1

图2

解设圆O 的半径为R， 则|PM| · |PN| = (R -|OP|)(R+|OP|)=R2-|OP|2=a2+4-|OP|2，将焦点三角形△PF1F2补成平行四边形PF1QF2， 再利用人教版必修4 课本109 页结论： 平行四边形对角线平方和等于一组邻边平方和的2 倍.4|PO|2+|F1F2|2= 2(|PF1|2+|PF2|2)，易得|PO|2=a2-2，所以|PM|·|PN|=6.

我们发现本题中|PM|·|PN| = |PF1|·|PF2|，这是一个巧合，还是一种必然? 是任意一个椭圆和圆都有这样的关系吗?

二、问题的探究

探究1如图3，椭圆圆O : x2+y2= r2(r ＞0)， 椭圆C 的左、右焦点分别为F1，F2，过椭圆上一点P 和原点O 作直线l 交圆O 于M,N 两点，若|PM|·|PN|=|PF1|·|PF2|，则r2的值为____.

解

根据平行四边形对角线平方和等于一组邻边平方和的2 倍的结论，易得

所以

由于|PM|·|PN|=|PF1|·|PF2|，根据① ②得r2=a2+b2.

通过探究1 发现，在椭圆中只有x2+y2=a2+b2的圆才具有这样的性质，我们知道圆锥曲线具有“家族特征”，在双曲线中是否存在这样的圆，具有类似的结论呢? 答案是肯定的.

图3

图4

探究2如图4，双曲线圆O : x2+y2= r2(r ＞0)，双曲线C 的左、右焦点分别为F1，F2，过双曲线上一点P 和原点O 作直线l 交圆O 于M,N两点，若|PM|·|PN|=|PF1|·|PF2|，则r2的值为____.

解

根据平行四边形对角线平方和等于一组邻边平方和的2 倍的结论，易得

所以

由于|PM|·|PN|=|PF1|·|PF2|，根据① ②得r2=a2-b2.

通过探究2 发现，在双曲线中存在圆x2+y2= a2-b2(a ＞b ＞0)具有这样的性质.

三、蒙日圆

从以上探究的结果可以看出，椭圆与双曲线都存在这样的一个圆，这个圆叫蒙日圆.这道圆锥曲线小题就是以蒙日圆为背景来命制的，蒙日是一名数学家，其生平简介可参见《数学2·必修》.

定理1过椭圆上任意不同两点A、B 作椭圆的切线，若切线垂直且相交于P，则动点P 的轨迹为圆x2+y2=a2+b2，该圆称为椭圆的蒙日圆.

证明①当题设中的两条互相垂直的切线中有斜率不存在或斜率为0 时，可得点P 的坐标为(±a,±b).②当题设中的两条互相垂直的切线中的斜率均存在且均不为0 时，设点P 的坐标是(x0,y0)(x0±a 且y0±b)，则过点P 的切线方程y-y0=k(x-x0)(k0).由

得

根据Δ=0 得

因为kPA,kPB是这个关于k 的一元二次方程的两个根，所以kPA·kPB=结合① ②得动点P 的轨迹为圆x2+y2=a2+b2.

定理2过双曲线上任意不同两点A、B 作双曲线的切线，若切线垂直且相交于P，则动点P 的轨迹为圆x2+y2=a2-b2，该圆称为双曲线的蒙日圆.

证法同椭圆的证法类似，留给读者自己证明.

定理3抛物线y2= 2px(p ＞0)上任意不同两点A、B作抛物线的切线，若切线垂直且相交于P，则点P 的轨迹是该抛物线的准线.

证明根据题意知道两条互相垂直的切线的斜率均存在且均不为0， 设点P (x0,y0)， 则过点P 的切线方程y-y0=k(x-x0).由

得

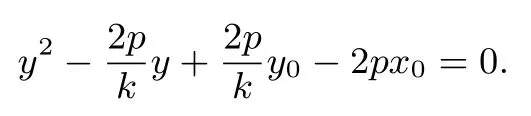
由Δ=0 得

因为kPA,kPB是这个关于k 的一元二次方程的两个根，所以所以动点P 的轨迹为准线

在抛物线上并不存在蒙日圆，其实蒙日圆对于我们来讲并不陌生，地方卷中曾经出现过它的身影，广大考生在备考中肯定“邂逅”过，只是没有引起注意和重视.

(1)求椭圆C 的标准方程;

(2) 若动点P (x0,y0) 为椭圆C 外一点， 且点P 到椭圆C 的两条切线相互垂直， 求点P 轨迹方程.答案： (1)(2)x2+y2=13.

四、启示

数学解题教学的核心思想就是引导学生把困难的、不熟悉的问题转化成容易的、熟悉的问题来解决.所谓学生熟悉的问题，除了熟悉解题的方法和策略外，重要的一环就是熟悉试题命制背景，由于高考试题都是原创题，学生若不熟悉题目的相关背景，特别是难题，会有一种莫名的“距离感”，解题时需要不断地尝试才能得到结果，时间成本很高，只有在解题教学时把每一道题的“背景”讲透了，应试时学生才会有心理优越感，才能居高临下看问题，才能准确领会命题者的意图，将问题快速解决.这就呼吁我们一线教师在解题教学时不能就事论事，要重视试题创作背景的讲解，让学生通过少量题目的训练达到掌握解决一类问题的策略和方法，避免题海，回归本质.