一个三角不等式的应用探讨

上海市上海交通大学附属中学嘉定分校(201821) 徐辉

图1

由上面不等式很容易得到：

(1)|sin x|≤|x|，x ∈ℝ，当且仅当x=0 时取等号;

一.用于比较大小

例1比较大小(1)sin 10°与

解可直接使用前述不等式.

例2设比较以下三个数的大小： sin(cos x)，cos(sin x)，cos x.

解显然所以sin(cos x) ＜cos x，又所以cos(sin x) ＞ cos x， 从而：sin(cos x)＜cos x ＜cos(sin x).

二.用于证明不等式

例3若x,y ∈ℝ，求证： |sin x-sin y|≤|x-y|.

证明

等号当且仅当x=y 时取得.

例4求证： |sin nx|≤n|sin x|，其中x ∈ℝ,n ∈ℕ∗.

解 方法1(数学归纳法)(1)当n=1 时，命题显然成立;(2)假设当n = k (k ≥1,k ∈ℕ∗)时，有|sin kx| ≤k|sin x|，则当n=k+1 时，

由(1)(2)，依数学归纳法原理知原命题成立.

方法2(迭代)(1)当n=1 时，命题显然成立;

(2)当n ≥1 时，

例5设求证：

证明因所以

注： 公式sin x ＜x ＜tan x 中，正弦最小，要证明正弦大于某数，可考虑将正弦转化为正切.

例6设求证：

解因故只需证明2x 即可.即要证：即而得证.

注： 此题再一次使用了将正弦转化为正切的思路.

三.用于证明等式

例7若x、y、z 中的每个数都恰好等于其余两数和的余弦.求证： x=y =z.

证明由题意x = cos(y + z)， y = cos(z + x)，z =cos(x+y)，若xy，则

矛盾.从而x=y，同理可得y =z，于是x=y =z(得证).

四.用于判断方程根的大小

例8设且α,β,γ 分别是三个关于x 的方程cos x = x,sin cos x = x,cos sin x = x 根， 试比较α,β,γ 的大小.

解(作差比较) 由题意，所以sin cos β ＜cos β，则

若α ≤β， 则cos α ≥cos β， 从而一方面α - β ≤0， 另一方面cos α - cos β ≥0， 与(∗) 矛盾.故α ＞β; 又若α ≥γ， 则cos α ≤cos γ， 但由知cos α ＜cos sin γ，即α ＜γ，矛盾，故α ＜γ.综上：β ＜α ＜γ.

五.引申出新的命题

例9已知函数f(x) = x cos x-sin x，求证： f(x)≤0;

解(1)当时，由x ≤tan x，知所以f(x)=x cos x-sin x ≤0，当且仅当x=0 时取等号;

例10设求证： 设

解可研究在上的单调性.对于任意且x1＜x2，显然有则故g(x) 在上的单调递减， 从而即

注： 本题例用了例9 的结论.

例11在锐角三角形ABC 中，求证：

(1)sin A+sin B+sin C ＞2;

(2)cos A+cos B+cos C ＞1.

证明(1) 由例10， 当时，即从而式相加可得sin A+sin B+sin

例12已知n ∈ℕ∗，

证明(1)由当时，有sin x ＜x ＜tan x.从而对任意n ∈ℕ∗，有相加得

故

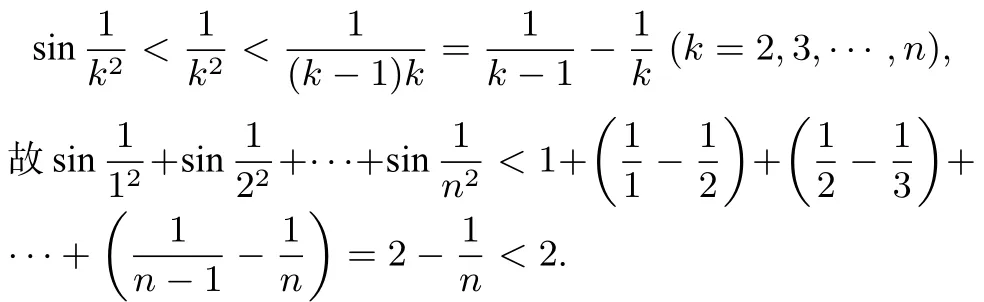
显然还可以继续缩小，可自行尝试.