求解Rosenau-KdV-RLW方程的线性化差分算法

李佳佳，王 希，张 虹，胡劲松

(西华大学理学院， 四川 成都 610039)

本文考虑如下一类Rosenau-KdV-RLW方程[1-3]的初边值问题：

ut-uxxt+uxxxxt+ux+uxxx+uux=0，x∈(xL，xR)，t∈(0，T]

(1)

u(x，0)=u0(x)，x∈[xL，xR]

(2)

u(xL，t)=u(xR，t)=0，uxx(xL，t)=uxx(xR，t)=0，t∈[0，T]

(3)

其中:u0(x)是一个已知的光滑函数。Rosenau-KdV方程[4-5]和Rosenau-RLW方程[6-7]经常用于描述紧离散系统。方程(1)在许多工程物理领域都有着广泛的应用，因此引起了众多学者关注。但这类方程很少有解析解，因此其数值研究具有重要的理论价值和实际意义。

由于线性化差分格式在计算过程中不需要迭代，从而比较节约计算时间。文献[8]对方程(1)提出了一个非线性守恒差分格式，但其数值计算需要迭代，耗费时间；文献[3]对方程(1)的广义形式进行了数值研究，本文对问题(1)—(3)提出一个新的具有二阶理论精度的三层线性化差分格式，运用离散泛函分析方法，证明了该格式的收敛性和稳定性。

1 差分格式及其可解性

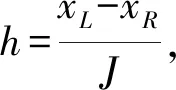
对问题(1)—(3)考虑如下有限差分格式：

(4)

(5)

(6)

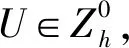
定理1.1若时间步长τ充分小，则差分格式(4)—(6)是唯一可解的。

证明用数学归纳法。显然U0是由初值条件式(5)唯一确定的，再用两层差分格式[10]计算出U1(即U0和U1是被唯一确定的)，假设Un(n≤N-1)是唯一可解的则

‖Un-1‖∞≤C，‖Un‖∞≤C

(7)

考虑方程(4)中的Un+1，有

(8)

将式(8)与Un+1作内积，由(6)、(7)式和分部求和公式[11]及引理1.1，有

(9)

又

(10)

将式(10)代入式(9)，整理有

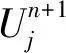
2 差分格式收敛性和稳定性

差分格式(4)—(6)的截断误差定义如下：

(11)

由Taylor展开，可知，当h，τ→0时，

(12)

引理2.1[10]设u0∈H2，则初边值问题(1)—(3)的解满足：

‖u‖L2≤C， ‖ux‖L2≤C， ‖uxx‖L2≤C， ‖u‖L∞≤C， ‖ux‖L∞≤C。

定理2.1 设u0∈H2，若时间步长τ和空间步长h充分小，则差分格式(4)—(6)的解Un以‖·‖∞收敛到初边值问题(1)—(3)的解，且收敛阶为O(τ2+h2)。

(13)

由引理2.1以及式(12)知，存在与τ和h无关的常数Cu和Cr，使得

‖un‖∞≤Cu；‖rn‖∞≤Cr(τ2+h2)，n=1，2，…，N

(14)

由初值条件(5)可得到以下估计式：

‖e0‖=0，‖U0‖∞≤Cu

(15)

再用具有二阶精度的两层差分格式[10]先计算U1，即可得到以下估计式：

(16)

这里C1为与τ和h无关的常数。

现在假设

(17)

其中Cl为与τ和h无关的常数。则由离散Sobolev不等式[11]和Cauchy-Schwarz不等式，有

(18)

(19)

整理得

(20)

由引理2.1以及微分中值定理，有

即

(21)

再取τ和h充分小，使

(22)

于是，由式(19)、(21)、(22)和引理1.1及Cauchy-Schwarz不等式有

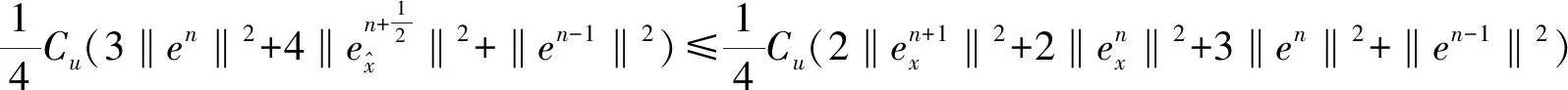
(23)

(24)

(25)

将式(23)—(25)代入式(20)，整理得

(26)

将式(26)从1到n递推求和，并整理有

(27)

又

(28)

将式(16)、(28)代入式(27)，利用离散Gronwall不等式[11]，取时间步长τ充分小以满足：

于是有

(Cn+1)2(τ2+h2)2(n=1，2，…，N-1)

其中

显然Cn+1为与n无关的常数。从而由归纳假设有

最后由离散Sobolev不等式[11]，有

‖en‖∞≤O(τ2+h2)，(n=1，2，…，N)

定理2.2 在定理2.1的条件下，差分格式(4)—(6)的解Un以‖·‖∞关于初值无条件稳定。