空间平行直线距离的高效安全计算

蒲方圆，何明星，刘 阳

(西华大学计算机与软件工程学院， 四川 成都 610039)

随着现代网络的迅速发展，多方合作的机会越来越多，如何保护各方隐私数据变得更加重要。安全多方计算是信息社会隐私保护的核心技术，是国际密码学界近年来的研究热点之一。安全多方计算的概念是由Yao[1]首先提出，是指在不泄露参与各方的输入数据(隐私性)的条件下，能正确完成对输入数据的函数计算(正确性)。它能够让人们最大程度地使用私有数据而不破环数据的私有性。正是因为此性质，它在数据隐私保护、电子商务、数据挖掘、保密存储、计算外包、密钥分配、入侵检测等方面有着广泛的应用[2-8]。文献[9-10]提出了通用的安全多方计算协议，即对任意的安全多方计算问题都转化为通用的安全多方计算协议来解决，并引入了安全多方计算的安全性形式化定义与模拟范例，但是对于解决一些具体问题而言，如果转化为通用的安全多方计算问题，计算复杂度和通信复杂度较高，使得效率较低，在实际中并不可行；所以具体问题应该使用具体的协议。

安全几何计算是安全多方计算的一个重要组成部分，它在商业、军事等方面拥有广泛的应用前景[11]。文献[11]提出了关于点面、线面、面面的位置关系判定协议。文献[12]提出了空间中基于阈值的点与线段之间距离关系的保密判定协议。文献[13]利用2组数据是否对应成比例，解决了空间点、线、面的相对位置判定。文献[14]提出了一个线段相交判定协议，同时研究了保护私有信息的多边形相交的判定协议。文献[15]提出了Paillier变体同态加密方案，并基于该方案提出了一种过私有2点保密计算出直线的协议。文献[16]提出了一种判定凸多边形的点包含协议，并进一步研究了凹多边形的点包含问题。文献[17]提出了判定任意多边形的点包含协议。文献[18]将有理数看作过原点的直线斜率，将有理数的运算转化为整数的运算，提出了有理数区间保密计算协议。

为了更加形象地说明本文要解决的问题，考虑以下场景，2家航空公司打算分别新开1条航线，已知这2条航线是相互平行的，为了保证飞机的飞行安全，现在要确定这2条航线的距离是否达到飞行的安全距离，如何在不泄露各自航线的基础上求得这2条航线的距离。此问题就是安全计算空间平行直线的距离。文献[19]提出了空间2平行直线间距离的保密计算协议，但是多次调用了不经意传输协议[20]和保密点积协议，增加了计算的复杂度和通信复杂度。

本文基于Paillier同态加密，提出了2个求空间平行直线的距离协议。协议1：针对交面式空间2平行直线设计了一个高效求空间平行直线距离的协议。协议2：针对标准式空间2条平行直线设计了一种新的、安全的求解空间2平行直线距离的协议。与文献[19]相比，协议1与协议2既不采用不经意传输协议，也不采用保密点积协议，使得计算复杂度和通信复杂度较低。

1 相关知识

1.1 安全性定义

1) 半诚实参与者[10]。假设所有的参与者都是半诚实的参与者，在协议的执行过程中，正确地按照协议的过程完成每一个步骤，不会随意篡改输入和输出信息，但可能会保存协议执行中关于其他参与者信息的中间结果，在协议结束后想要推导出其他参与者的私有信息。

定义如果存在概率多项式时间模拟器S1，S2使得以下2个等式同时成立

(1)

(2)

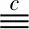
1.2 Paillier同态加密方案[21]

该加密方案由密钥生成(Gen)、加密(Enc)和解密(Dec)这3个随机算法组成。

Enc: 选择随机数r，r

Dec: 计算密文c的明文为

Paillier加密方案的同态性，为

E(m1)×E(m2)=E(m1+m2)

E(m)t=E(tm)

2 保密计算交面式的2条空间平行直线的距离

2.1 问题描述

设Alice和Bob分别拥有2条空间平行直线，其方程分别为

问题是如何保密计算2平行直线的距离d(考虑b1c2-b2c1≠0 的情况)。

当b1c2-b2c1≠0时，空间2交面式平行直线间的距离为d。

(3)

式中n1，n2是l1对应平面π1，π2的法向量。

2.2 保密计算交面式2条空间平行直线的距离(协议1)

输入：Alice拥有1条保密直线

Bob拥有1条保密直线

输出: Alice和Bob计算得到直线l1，l2之间的距离d。

1)基于Paillier的同态加密方案(G，D，E)，Alice运行算法(Gen)生成同态加密的密钥对(pk，sk)，并公布pk。

2)Alice用生成的公钥对b1，c1，d1，b2，c2，d2进行加密，得到E(b1)，E(c1)，E(d1)，E(b2)，E(c2)，E(d2)，并发送给Bob。

3)Bob选择随机数k1，k2，并计算E(k1)，E(k2)和Q1，Q2，将Q1，Q2发送给Alice(其中α=c3d4-c4d3，β=b4d3-b3d4，γ=b3c4-b4c3)。

Q1=E(b2)α×E(c2)β×E(d2)γ×E(k1)=E(b2α+c2β+d2γ+k1)

(4)

Q2=E(b1)α×E(c1)β×E(d1)γ×E(k2)=E(b1α+c1β+d1γ+k2)

(5)

4)Alice用私钥解密Q1，Q2，得到q1，q2，并发送给Bob。

5)Bob得到q1，q2后，计算Aa1，Aa2，Q3，Q4。将Q3，Q4发送给Alice。

Aa1=q1-k1

(6)

Aa2=q2-k2

(7)

(8)

(9)

6)Alice计算d2，将结果d发送给Bob。

(10)

2.3 协议的正确性

定理1 协议1能正确计算出交面式的2条空间平行直线的距离。

证明Alice的密文信息为:

Bob的密文信息为

Bob根据密文信息计算Q1，D(Q1)，为

Q1=E(b2)α×E(c2)β×E(d2)γ×E(k1)=

[gb2α+c2β+d2γ+k1(r1r2r3r4)N]modN2

Bob按式(6)、式(8)计算出Q3，并发送给Alice。同理Alice可得到Q4，按式(10)计算平行直线距离的平方。

故有

由以上可知，协议1能够正确地计算出2条空间平行直线的距离。在整个过程中，Alice和Bob没有泄露各自的秘密信息，而且完成了平行直线的距离计算。

2.4 协议的安全性

定理2 在半诚实模型下，协议1是安全的。

证明对Alice而言，Alice在协议过程中获得

q1=b2α+c2β+d2γ+k1

q2=b1α+c1β+d1γ+k2

在这4个等式中，b1，b2，c1，c2，d1，d2是Alice的保密数，α，β，γ，k1，k2是5个未知变量，不能根据这4个等式来确定5个变量的值，并且α，β，γ与Bob的保密数b3，b4，c3，c4，d3，d4有这样的关系:α=c3d4-c4d3，β=b4d3-b3d4，γ=b3c4-b4c3，因此Alice得不到关于Bob的任何私有信息。

对Bob而言，Bob在协议1的过程中获得关于Alice的保密数E(b1)，E(c1)，E(d1)，E(b2)，E(c2)，E(d2)，由于Paillier加密方案的安全性，Bob在不知道Alice的私钥的条件下不能得到Alice的保密数。Bob得到式(6)、式(7)和式(10)这3个等式，其中a1，a2，b1，b2，c1，c2，d1，d2是关于Alice的8个未知变量，根据数学知识，不能通过这3个等式来确定8个变量的值，则Bob得不到关于Alice的任何信息，因此协议1是安全的。

下面再通过构造模拟器的方法进行具体的安全性证明。

通过构造满足等式(1)和(2)的模拟器S1，S2来证明。

构造S2对于输入(l2，f2(l1，l2))，S2按以下方式运行。

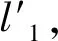
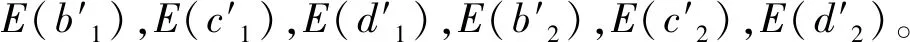
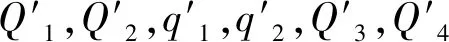
4)S2计算d2，则d为空间2条平行直线l1，l2间的距离。

令

由于在协议1的执行过程中

同理，用类似的方法可以构建模拟器S1使得

3 保密计算标准式空间2平行直线的距离

3.1 问题描述

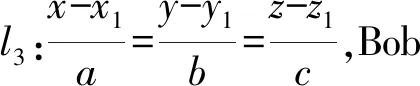
问题是在Alice和Bob不泄露各自直线上的任何一点的情况下计算2直线的距离。

(11)

3.2 保密计算标准式2条空间平行直线的距离(协议2)

输出:Alice和Bob计算得到2直线之间的距离d。

1)基于Paillier的同态加密方案， Alice生成密钥对(pk，sk)，并公布pk。

2)Alice在直线l3选取保密点A(x1，y1，z1)，Bob在直线l4选取B(x2，y2，z2)。

3)Alice 计算:

e1=2(-x1c2-x1b2+y1ab+z1ac)

(12)

e2=2(x1ab-y1c2+y1a2+z1bc)

(13)

e3=2(x1ac+y1bc-z1a2-z1b2)

(14)

e4=(y1c-z1b)2+(z1a-x1c)2+(x1b-y1a)2

(15)

Alice用自己的公钥对e1，e2，e3进行加密得密文:E(e1)，E(e2)，E(e3)。Alice将密文发送给Bob。

4)Bob计算e5，用Alice公钥加密e5得E(e5)，再计算M′并把M′发送给Alice。

e5=(z2b-y2c)2+(x2c-z2a)2+(y2a-x2b)2

(16)

M′=E(e1)x2×E(e2)y2×E(e3)z2×E(e5)

(17)

5)Alice解密M′得到m′，并计算m′+e4，进而可得d，再将结果d发送给Bob。

(18)

3.3 协议的正确性

定理3 协议2能正确计算出标准式的2条空间平行直线的距离。

证明证明过程省略了初始化，Alice和Bob的密文信息分别为：

Alice的密文信息

Bob的密文信息

Bob根据密文信息计算M′。

(ge1x2+e2y2+e3z2+e5(r5r6r7r8)N)modN2

Bob将M′发送给Alice，Alice解密可得D(M′)。

然后根据公式(18)计算d，故有

由以上证明可知，协议2能够正确地计算2条空间平行直线的距离。整个过程中，Alice和Bob没有泄露各自的秘密信息，且完成了平行直线距离的计算。

3.4 协议的安全性

定理4 在半诚实模型下，协议2是安全的。

证明首先考虑Alice的计算安全性，第3)步Alice将密文E(e1)，E(e2)，E(e3)发送给Bob，根据Paillier加密系统的语义安全，Bob没有Alice的私钥，则Bob不能得到Alice的信息。因此，Bob不能得到任何关于Alice的私有信息。

其次考虑Bob的计算安全性。第4)步， Bob发送给Alice密文M′，对M′解密得到m′，其中m′=e1x2+e2y2+e3z2+e5，但x2，y2，z2都是未知数，根据数学知识，不能根据这一个等式来确定这3个未知数的值，则Alice不能得到任何关于Bob的信息。所以，协议2的每一步都是隐私保护的。下面构造模拟器进行具体的证明。

构造满足等式(1)和(2)的模拟器S3，S4来证明协议2的安全性。

构造S3对于输入(l3，f3(l3，l4))，S3按以下方式运行：

3)S3计算E(e1)，E(e2)，E(e3)；

4)S3计算M″

5)S3解密得到m″，并计算m″+e4。

同理，用类似的方法可以构造模拟器S4使得

4 协议效率分析与比较

4.1 计算复杂度

上述文献的协议中有的使用了公钥加密算法，有的未使用公钥加密算法。为了方便比较，将模指数运算的次数作为衡量计算复杂度的指标，忽略准备工作和随机数选择的计算开销。

Paillier同态加密算法中进行1次加密运算需要做2次模指数运算，1次解密运算需要做1次模指数运算，每进行1次密文模指数运算为1次模指数运算。为了方便计算，忽略准备工作和随机数选择的计算开销。

文献[19]没有明确表明使用哪个具体的不经意传输协议和保密点积协议，所以本文在进行算法比较时采用文献[20]的不经意传输协议，保密点积协议也采用该文献的不经意传输方法。1次保密点积协议需要调用m次1-out-of-k不经意传输，1次1-out-of-k不经意传输至少需要logk次1-out-of-2不经意传输，1次1-out-of-2不经意传输至少需要2次模指数运算，那么1次不经意传输协议至少需要2logk次模指数运算，1次点积协议至少需要2mlogk次模指数运算(其中m是安全参数)。文献[19]调用了6次不经意传输协议和6次点积协议，则至少需要12(m+1)logk次模指数运算。根据实际意义，只有当m>5且k>8才能达到基本安全级别。在协议1中，Alice需要加密6次和解密2次， Bob需要加密2次和6次密文模指数运算，需要进行24次模指数运算。在协议2中，Alice需要加密3次和解密1次，Bob需要加密1次和3次密文模指数运算，需要进行12次模指数运算。

4.2 通信复杂度

通常情况下，衡量通信复杂度的方法是比较协议交换信息的比特数或比较通信的轮数，本文使用通信轮数来衡量。文献[19]协议通信轮数为 6(m+1)次，本文协议1通信轮数为5次，协议2通信轮数为3次。由于本文未使用不经意传输协议和保密点积协议，所以没有基础协议的交互过程，通信次数大大减少。

表1 几个协议的性能比较

从表1可以看出，本文不管是计算复杂度，还是通信复杂度均优于文献[19]的协议。

为了进一步对协议进行性能分析，使用Java编程语言对3种协议分别进行了编程实现。计算机环境：操作系统为windows 7 企业版，处理器为Inter Core(TM)i5-2 450 M 2.50 GHz，内存为4 GB。实验中设定Paillier加密算法中使用的大素数p和q的位数为512 bits，其中k=9、m=6，保密数的范围设定为[1，30]。并对每种协议的实验结果随机抽取20组数据求时间平均值，其结果如表2所示。

表2 协议的运算耗时对比

实验结果表明，文献[19]中的协议需要的运行时间远远大于本文提出的2个协议。

5 结束语

本文在半诚实模型下，在Paillier同态加密算法的基础上，分别提出了标准式空间2平行直线距离和交面式空间2平行直线距离的安全计算协议，同时证明了协议的正确性和安全性。 在今后的工作中，将探讨恶意模型下空间2平行直线距离的安全计算问题。另外，对于空间任意2条直线，将进一步研究2条直线上点的最小距离的安全计算问题。