非自治Plate方程指数吸引子的存在性
2019-07-11苏小虎姜金平王力杰
苏小虎,姜金平,王力杰
(延安大学数学与计算机科学学院,陕西延安716000)
本文主要讨论下面的非自治Plate方程
(1)
其中Ω⊂Rn是光滑边界上的有界区域;u=u(x,t)是Ω×(τ,+∞)上的未知函数;α>0为粘性阻尼;f是Lipschitz连续函数,并且满足下列条件
f(0)=0,f′(s)≥-λ1,
(2)
C1Sp-C0≤f(s)s≤C2Sp+C3,p≥2,
∀s∈R。
(3)

(4)
其中M>0,Ci>0,i=1,2,…。
关于Plate方程的研究已经有一些结果,文献[1]研究了带有非线性阻尼Plate方程的全局吸引子;文献[2]研究了带有非线性阻尼Plate方程的一致吸引子;文献[3,4]作者分别研究了具有局域阻尼和无界域临界指数的Plate方程的全局吸引子和指数吸引子;文献[5]研究了具有临界指数的Plate方程的渐近性和正则性;在文献[6]作者研究了当满足周期和拟周期及其他条件,f(u)满足临界增长时指数吸引子的存在性;文献[7]研究了g∈L∞(R,L2(Ω)时指数吸引子的存在性;文献[8]研究了当g(t)满足Hödler连续,f(u)满足临界增长时指数吸引子的存在性。
本文在阅读文献[6-9]过程中受到启发,在光滑边界上的有界区域Ω⊂Rn上,非线性项f(u)满足任意增长时,外力项g(x,t)满足平移有界条件下,证明非自治Plate方程指数吸引子的存在性。
1 预备知识
定义1[8](非自治指数吸引子)紧集族{M(t),t∈R}是Banach空间E上的过程族{U(t,τ),τ∈R}的(非自治)指数吸引子。如果所有集合M(t)的分形维数是有限的,即dimF(M(t),E)≤C<∞,∀t∈R;
(i)对t≥τ,τ∈R,M(t)是正不变的:U(t,τ)M⊂M;
(ii)存在常数α>0,递增函数Q(·),使得对∀t∈R,S≥0以及E中的任意有限子集B,有
dimE(U(t+s),t)B,
M(t+s))≤Q(BE)e-αs。
定义2[8]设E是Banach空间,E1是空间E上的紧嵌入,又B是E1中的有界子集,对于常数0≤ε≤1,δ,K>0,定义如下非线性算子S:E→E的一个类Sδ,ε,K(B):
(i)S映射B中的一个δ领域Qδ(B)到B,S:
Qδ(B)→B,其中δ领域赋予E1中的拓扑结构。
(ii)我们把S分解为下面的形式
S=S0+S1,
S0:Qδ(B)→E,S1:Qδ(B)→E1,
其中S0,S1满足下列情形
S0(z1)-S1(z2)E≤εz1-z2E,
∀z1,z2∈Rδ(B),和
S1(z1)-S1(z2)E1≤Kz1-z2E1,
∀z1,z2∈Qδ(B)。
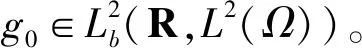
Ug(t,τ)uτ2≤M0,
∀t-τ≥TB,uτ∈B,g∈∑。
(5)

Ug(t,τ)uτ2≤M,∀t≥τ,uτ∈B。
由定义3结合问题(1),我们把Ug(t,τ)uτ=
u(t)可分解为
Ug(t,τ)uτ=D(t,τ)uτ+Kg(t,τ)uτ。
(6)
这里的D(t,τ)uτ=v(t),Kg(t,τ)uτ=w(t)分别是下列方程的解。
(7)
以及
(8)
引理1[7]对∀τ∈R,方程(1)的解满足:存在一个常数k0,使得对∀t≥τ,
D(t,τ)uτ2≤Q1(uτ)e-k0(t-τ)
(9)
其中Q(·)为区间[0,∞)上的增函数,并且k0依赖于τ的。
定理1[8]设E和E1都是Banach空间,并使E1紧嵌入到E,B是E1中的一个有界集U(t,τ)(τ∈R,t≥τ)是在空间E中的过程。设U(t,τ)满足
(1)存在常数ε∈[0,1]以及K>0,T>0,使得U(T+τ,τ)∈Sδ,ε,K(B),∀τ∈R;
(2)U(T,τ)是Hölder连续:存在常数k1及CT,B,有zi∈Qδ(B)(i=1,2,S∈[0,T]),
使得
U(τ+s+t,τ)z1-U(τ+t,τ)z1E≤
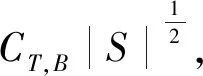
(10)
以及
U(τ+s+t,τ+s)z2-U(τ+t,τ)z2E≤
CT,Bectsk1,∀t≥T
(11)
则存在指数吸引子τ→εU(τ)⊂Qδ(B),τ∈R。并且这里满足以下性质
(i)吸引子εU(τ)⊂B,(τ∈R),并且其分形维数有限
dimF(εU(τ),E)≤C1;
(12)
其中C1是不依赖于τ的常数。
(ii)关于U的集族εU是正不变的,
U(t,τ)εU(τ)⊂εU(t),∀t,τ∈R,t≥τ;
(13)
(iii)集族有如下指数吸引子的形式
distE(U(t,τ)B,εU(t))≤
C2e-α(t-τ),∀t≥τ;
(14)
其中C2和α是不依赖于t和τ的常数。
(iv)函数t-εU(t)是一致Hölder连续的

C3sk,∀t∈R。
(15)
其中C3和k是不依赖于t和s的常数。
2 主要结果及证明
引理2[10]设u(t)是方程(1)的一个解,则对于∀ε>0及τ∈R,存在正常数Cε,Kε使得
u(t)=v1(t)+w1(t),∀t≥τ,
(16)
其中u1(t),w1(t),满足下面的估计
-△w1(t)2≤Kε,∀t≥τ,

(17)
其中的Cε,Kε是不依赖于τ的常数。
引理3 设引理1成立,则存在一个正常数M,使得对于V中的任意有界子集B⊂D(A),有T=
T(B)>0成立。
Ug(t,τ),uτ2≤M,∀t-τ≥T,uτ∈B。(18)
证明在定义3中我们可以知道,存在常数TB(TB是依赖于B的),使得
Ug(t,τ),uτ2≤M0,∀t-τ≥TB,∀uτ∈B
(19)
我们用△ut与(1)式做内积,得到
(f(u),△ut)=(g(x,t),△ut),
(20)
又因为
则由上式得
(21)
其中
(22)
再由(2),(3)我们可得

Cλ1▽u2·△u。
(23)
将(22)和(23)代入(20),我们整理得
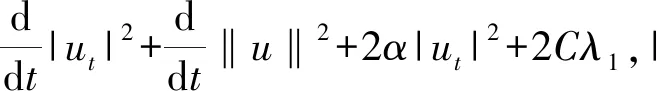
引理4 由定理1确定的时间T>0,过程族Ug(t,τ)在以下条件是满足Hödler连续的:则存在常数CT,B及c′,使得对∀zi∈Qδ(B)(i=1,2),s∈[0,T]是Hödler连续的。
U(τ+s+t,τ)z1-U(τ+t,τ)z1E≤
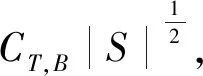
(24)
以及
U(τ+s+t,τ+s)z2-U(τ+t,τ)z2E≤
CT,BectSk1,∀t≥T
(25)
证明由定义3以及(1)式知u(t)=Ug(t,τ)uτ(t≥τ)满足:对于∀uτ∈Q1(B),
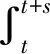
(26)
这里的MB是和Q1(B)有关的常数。对∀s∈[0,T]和z2∈Q1(B)有
Ug(τ+s+t,τ)z1-Ug(τ+t,τ)z1=
(27)
因此,我们有
U(τ+s+t,τ+s)z2-U(τ+t,τ)z2E≤
Ug(τ+s+t,τ+s)(Ug(τ+t,τ+s)z2)-
Ug(τ+t,τ+s)z2+Ug(τ+t,τ+s)z2-
Ug(τ+t,τ+s)(Ug(τ+s,τ)z2)。
(28)
结合(24)和(26)得证。
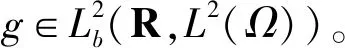
(29)
引理6 由定理1,存在T=T(B),使得Ug(t,τ)(t≥τ)满足以下几条性质
(i)对∀τ∈R,t≥0有
ug(t+T+τ,τ)Q1(B)⊂B;
(30)
(ii)对于∀z1,z2∈Q1(B)以及τ∈R,Ug(t+τ,τ)可分解
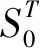
∀z1,z2∈Q1(B),
(31)

∀z1,z2∈Q1(B)。
(32)
证明由引理3可知,对于初值uτ∈Q1(B),用S(t,τ)uτ表示下面方程的解
utt+αut+△2u+f(u)=0,
在这里我们设


(33)
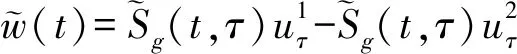
(34)
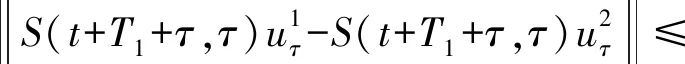

(35)
由引理2,对于D(A)中的有界集Q1(B),存在常数T2(依赖于B),使得∀τ∈R有
Ug(t,τ)Q1(B)⊂B,∀t-τ≥T2。
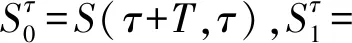


证明:由引理4和引理6,对于集合B和满足条件(4)的外力项g(x,t),则(1)中存在一个自治的指数吸引子{εg(t)}t∈R。
