基于刚柔耦合的变排量齿轮式机油泵振动特性分析
2019-07-10陆国平刘许兵
陆国平,刘许兵
(1.南京汽轮电机(集团)有限责任公司,江苏南京 210037;2.上海工程技术大学机械与汽车工程学院,上海 201620)
0 引言
机油泵作为汽车发动机润滑系统的重要组成部分,对发动机的正常运行起着至关重要的作用。与定排量机油泵相比,变排量机油泵可根据发动机的实际工况进行油量调节,能有效提高发动机的能耗利用率。研究发现:当发动机采用变排量机油泵时,其能源消耗量与CO2排放量可有效降低3%[1]。目前,变排量机油泵主要分为转子式、齿轮式与叶片式。变排量齿轮式机油泵因具有成本低、控制精确、转速可调控范围大的优点而受到了工业应用与科学研究的广泛关注[2]。
目前,齿轮式机油泵的研究主要集中在压力波动、流量、空化等方面,然而鲜有涉及其动力学性能的研究。变排量齿轮式机油泵通过改变齿轮间啮合位置来实现供油量的变化,为此,其动力学特性对机油泵的整机耐久性具有重要的影响,且会进一步影响机油泵的工作特性及发动机润滑系统的正常运行。因此,变排量齿轮式机油泵动力学特性的研究具有重要的意义。
近年来,齿轮式机油泵动力学特性的研究主要集中在刚体动力学模型的建立及分析,然而该模型的建立忽略了高速运行过程中齿轮泵的微变形导致的不平稳冲击,进而导致较大的误差,故不适用于机油泵高转速的工况[3]。为此,变排量齿轮式机油泵的刚柔耦合动力学模型的建立及分析至关重要。
目前,基于多柔体动力学理论,学者们提出了刚柔耦合动力学理论,并展开了大量的研究,已应用到齿轮传动系统动力学分析问题上[4-6]。李增彬[4]采用ANSYS软件建立了激振横梁的有限元模型,并通过计算生成模态中性文件,建立了惯性振动筛的刚柔耦合模型,获得了筛箱质心位移曲线并验证了模型的有效性。邱星慧等[5]以地铁齿轮箱实体模型为研究对象,基于ADAMS软件用柔性体替换原模型中对应的刚形体,建立齿轮接触模型,生成刚柔耦合动力学模型,分析了齿轮启动瞬间及较大冲击时箱体各点的振动冲击响应,并对刚体结构进行了优化。然而仍鲜有涉及齿轮泵的刚柔耦合动力学分析,且未对齿轮泵工作过程中的动力学特性与振动特性关系进行分析。
基于刚柔耦合动力理论,本文作者采用ANSYS软件对变排量齿轮式机油泵的关键部件——主从动齿轮进行柔性化建模,建立刚柔耦合动力学模型,对机油泵高速下的稳态工况进行仿真分析,并将其应用于振动特性分析。
1 变排量齿轮式机油泵结构参数
文中选用的变排量齿轮泵属于两级压力泵,其结构如图1所示。当发动机转速低于3 500 r/min时,发动机处于低压状态,输出油压为0.18 MPa;转速高于3 500 r/min时,油压切换为高压,输出油压达到0.33 MPa。供油量的调节是通过泵齿轮的相对位移改变而实现的,当泵齿轮全啮合时,供油能力最强,随着从动齿轮轴向位移的增大,供油能力逐渐降低。
变排量齿轮泵的核心部件为主从动齿轮,以泵齿轮为研究对象建立刚柔耦合动力学模型。主从动齿轮的具体参数为:中心距L为29.6 mm,齿数z为10,模数m为2.75 mm,压力角为20°,分度圆直径d为27.5 mm。基于刚柔耦合动力学理论,建立了该泵的刚柔耦合动力学模型,并在发动机高转速7 000 r/min与稳态工况下进行了刚柔耦合动力学仿真分析。
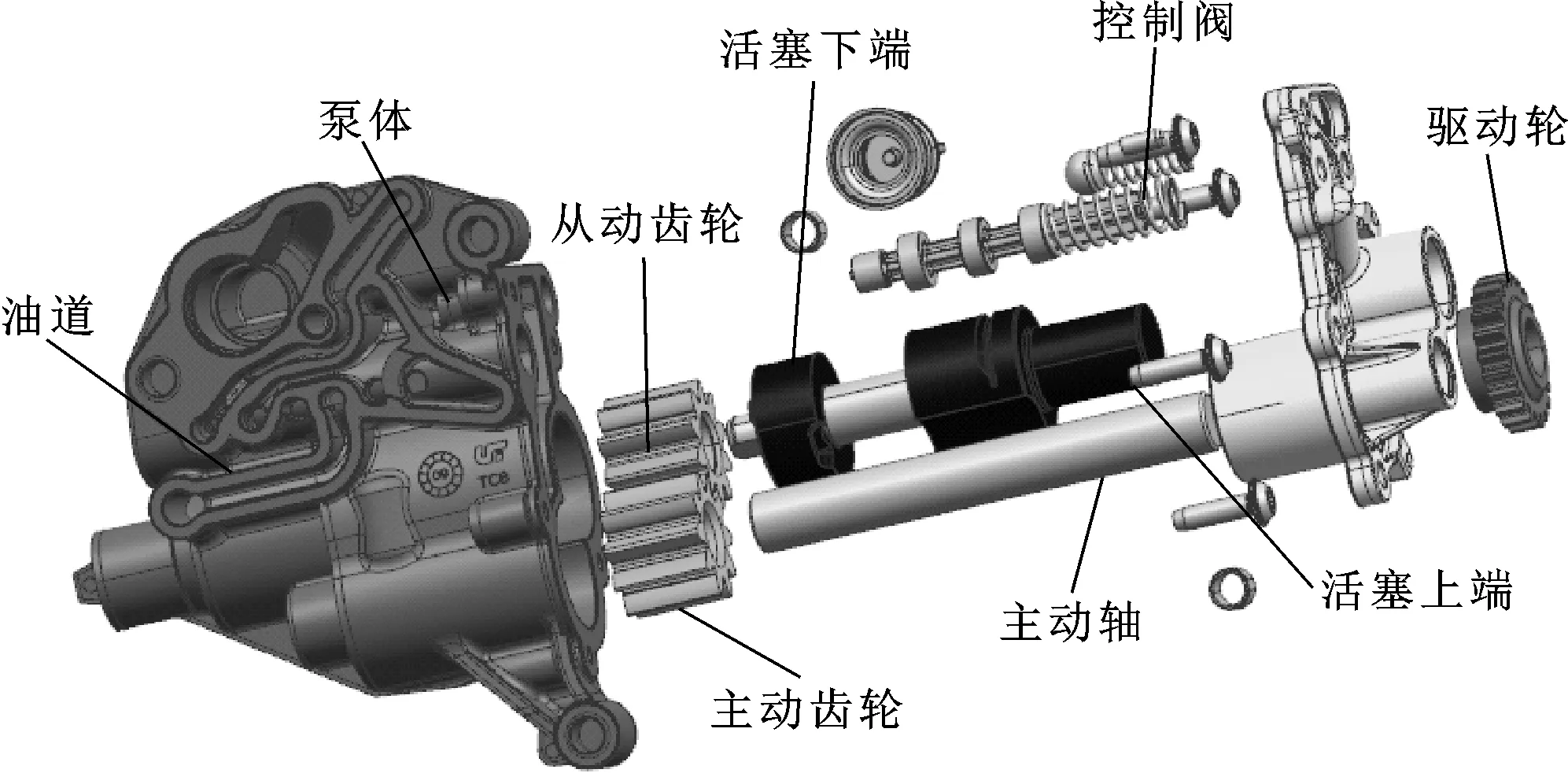
图1 变排量齿轮式机油泵结构简图
2 刚柔耦合动力学模型
2.1 刚柔耦合动力学理论
柔性体作为变形体,其内部各点的相对位置会随着变形的改变而发生变化,为此,采用弹性坐标定义弹性体各点的坐标。通常,将柔性体的运动过程分解为刚性移动与转动及变形运动3个过程[7],如图2所示。考虑节点P变形前后的方向、位置及模态的改变,柔性体的广义坐标可定义为
ξ=[x,y,z,ψ,θ,φ,qi(i=1,2,......,M)]T=
[r,ψ,q]T
(1)

图2 柔性体变形模型及节点P坐标
柔性体的动能T和势能W的广义表达式分别为
(2)
(3)
式中:M(ξ)为质量矩阵;K为对应于模态坐标q的构件广义刚度矩阵。
柔性体运动方程可由拉格朗日方程推导出:
(4)
ψ=0
(5)
式中:ψ为约束方程;λ为约束方程的拉氏乘子;ξ为式(1)定义的广义坐标;Q为投影到ψ上的广义力;L是拉格朗日项;Γ是能量损耗函数。
联和式(2)(3)(4)得到的运动微分方程为
(6)
式中:M为柔性体质量矩阵;K为广义刚度矩阵;fg是柔性体的重力。
2.2 刚柔耦合动力学模型建立
文中将对变排量齿轮式机油泵进行刚柔耦合动力学的分析,其流程如图3所示。多刚体动力学模型的建立在前期的相关研究中已报道[8]。本文作者将依据模态参数法对高转速下主、从动齿轮进行柔性体建模,随后确定相关构件间的约束关系,建立刚柔耦合动力学模型,进一步进行动力学分析。

图3 刚柔耦合动力学分析流程
2.2.1 柔性体建模
利用ANSYS软件将研究对象微型变位齿轮离散成网格单元,进行模态计算,并通过ADAMS软件读取计算得到的模态中性文件(MNF)以完成柔性体的导入。主动齿轮柔性体建模过程如下:
(1)导入几何模型
将主动齿轮的几何模型导入ANSYS软件,然后调整模型的轴线方向使其与机油泵的安装方向一致。
(2)定义质量单元
对齿轮实体进行单元类型的定义,其中实体单元选用Brick 8 node 185单元,质量单元选择MASS21单元,其中实常数取值一般偏小,统一为1×10-6。
(3)设置材料参数
主从动齿轮的材料统一为钢材,且在利用ANSYS与ADAM软件进行仿真时,单位统一。具体如下:弹性模量设为2.07×105MPa,泊松比为0.29,密度为7.8×10-6kg/mm3。
(4)划分网格
选用实体单元Brick 8 node 185对齿轮进行网格划分,且将网格精度的级别设置为3(网格精度过高,求解时间越长,仿真结果可信度越高[9]),其结果如图4所示。

图4 齿轮网格划分示意图
(5)创建关键点
采用质量单元对关键点进行网格划分,建立外节点,以确保齿轮柔性体模型与其他结构的连接。在ADAMS软件中,以上外节点将自动生成该模型建立需要的标记点,进一步确立柔性体与其他构件的约束关系。
(6)确定刚性区域
刚性区域是指与外界连接且不发生变形的区域。文中涉及到的主、从动齿轮均为圆柱直齿齿轮,因此选取齿轮的内圆柱面作为刚性区域,如图5所示。

图5 创建刚性区域后的齿轮有限元模型
(7)生成模态中性文件
选取主动齿轮的前10阶模态,其模态中性文件如图6所示。

图6 齿轮的模态中性文件
通过以上步骤建立了主动齿轮的柔性体模型,将它与其他部件进行连接,建立刚柔耦合动力学模型。考虑到从动齿轮的齿形、结构参数及刚性区域基本相同,主、从动齿轮的刚柔耦合动力学模型可通用。
2.2.2 刚柔耦合动力学建模
基于变排量齿轮式机油泵的多刚体动力学模型及主从动齿轮柔性体模型,定义了柔性体模型间及柔性体与刚性构件间的约束关系,并确定相应的驱动及负载,建立起的变排量齿轮式机油泵刚柔耦合动力学模型如图7所示。
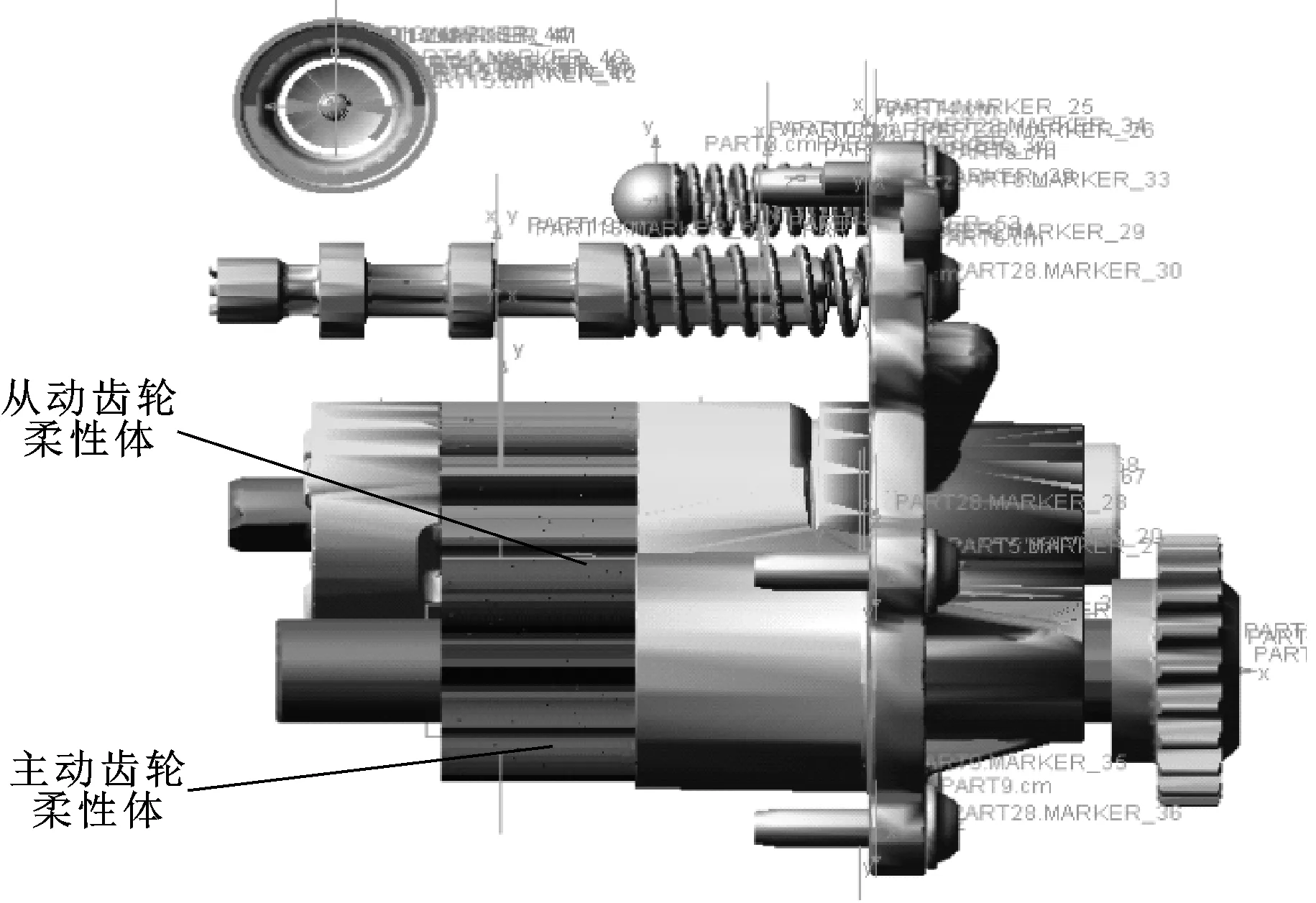
图7 变排量齿轮式机油泵刚柔耦合动力学模型
2.2.3 实验验证
变排量齿轮式机油泵多刚体模型的建立忽略了高速运行过程中齿轮泵的微变形导致的不平稳冲击,进而导致高速时存在较大的误差。为了验证以上刚柔耦合动力学模型,本文作者进行了变排量齿轮式机油泵综合性能的台架试验,选择发动机高转速7 000 r/min下的实验数据与仿真结果进行比较与分析,如图8所示。
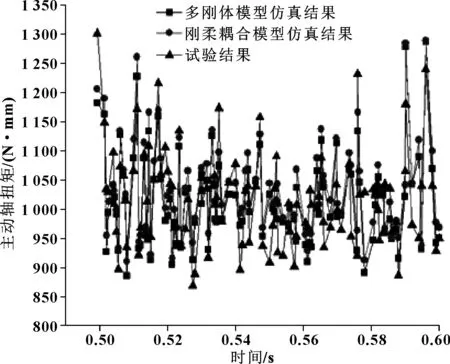
图8 变排量齿轮式机油泵实验与仿真
由图8可以看出:该机油泵的主动轴扭矩实验曲线、多刚体动力学模型仿真曲线及刚柔耦合动力学模型仿真曲线的趋势能够较好地吻合,然而该机油泵的主动轴扭矩实验值最大,多刚体动力学模型仿真结果最小,刚柔耦合动力学模型仿真结果介于中间,与实验值更为接近。以上实验结果说明,该机油泵的刚柔耦合动力学模型是合理的,能够准确反映该机油泵在高转速下的工作特性。
为了进一步验证该机油泵刚柔耦合动力学模型的准确性,采用该模型仿真分析了该机油泵在稳态工况7 000 r/min下齿轮切向力的时域及频域图,如图9与图10所示,可以看出在高转速下该机油泵主动齿轮的径向力波动及误差更小,仅在频域图的一倍频率附近出现激振,且其幅度远小于多刚体动力学模型仿真结果中的激振。相比于多刚体动力学模型,该机油泵的刚柔耦合动力学模型的均值更接近于理论值,说明该机油泵的刚柔耦合动力学模型的仿真结果更接近理论结果。
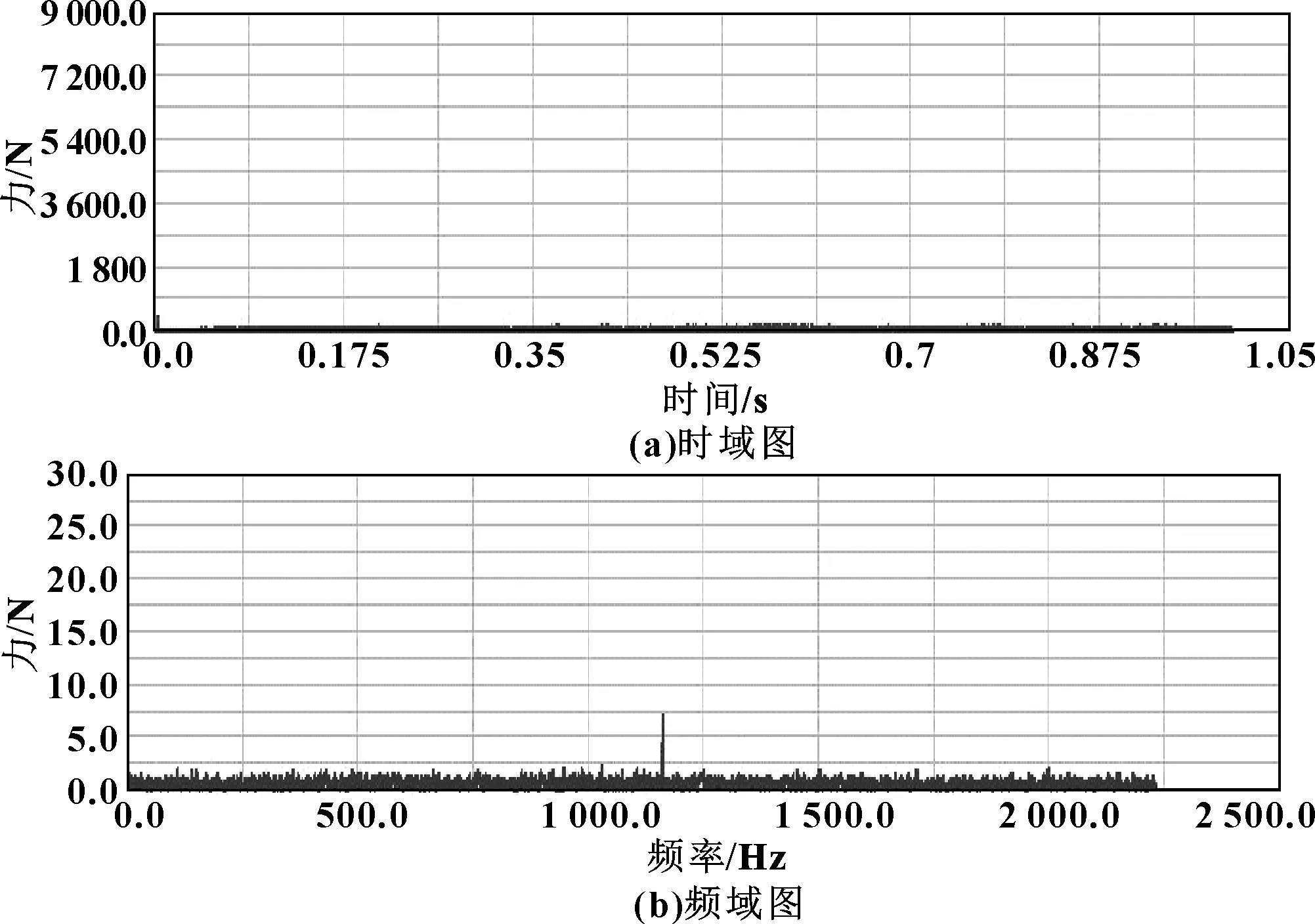
图9 工况7 000 r/min下主动齿轮径向力的时域图和频域图

图10 主动轮径向力仿真和理论对比
3 变排量齿轮式机油泵振动特性分析
结合上述刚柔耦合动力学模型及仿真分析,首先确定了该机油泵振动激励的大小与方向,随后在目标部件上建立输入与输出通道,将振动激励通过输入通道加载,由输出通道输出系统响应,建立了研究对象的振动分析模型,该仿真计算的初始和终止频率分别设定为0.01与50 000 Hz,步长为10 000。
该机油泵的系统模态分布如图11所示,计算可得该机油泵系统共51阶模态,其中前12阶为过阻尼,其余为欠阻尼,且第13、14阶所对应的频率分别为0.02与0.22 Hz,属于低频区。在正常转速下,该机油泵的激振频率为100.00~1 166.67 Hz,说明该机油泵的固有频率与齿轮副的激振频率相差较大,为此可以得出在工作过程中该机油泵的激振频率不会造成系统共振。
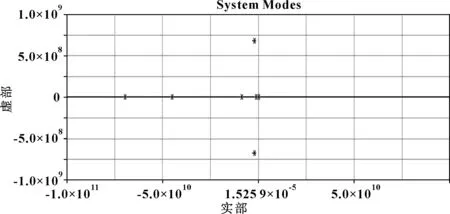
图11 变排量齿轮式机油泵的系统模态分布
表1列出了关键柔性体——主、从动齿轮的前11阶固有频率,可以得出系统第15阶模态数据与从动齿轮模态中性文件的第16阶模态数据相近,容易激起该阶模态,进而引起从动齿轮发生局部共振,为此,需调整该机油泵的模型结构或采用隔振技术降低振动强度。以上分析可为该机油泵的优化设计提供理论指导。

表1 柔性部件固有频率表
4 结论
基于变排量齿轮式机油泵工作原理与多刚体动力学模型,通过该机油泵的虚拟样机建立了刚柔耦合动力学模型,得出以下结论:
(1)首先对该泵传动系统的关键部件——主、从动齿轮进行了柔性体建模,成功建立了该泵的刚柔耦合动力学模型,用来解决齿轮传动系统高转速下微变形而产生的不平稳冲击。
(2)该机油泵综合性能的台架试验结果与以上模型的仿真结果相吻合。与多刚体动力学模型相比,该刚柔耦合动力学模型的结果与实验值更相近,误差较小,验证了该刚柔耦合动力学模型的合理性。
(3)基于以上模型,确定了该机油泵的振动激励大小与方向,建立了振动分析模型。通过系统模态分析得出该机油泵的主动齿轮、驱动轮最易发生振动疲劳破坏,且从动齿轮的模态中性文件的第16阶模态与系统模态最接近,易发生局部振动。以上结果为该机油泵的结构优化及运行维护提供了一定的理论依据。
