一类非自治连续型竞争系统的概周期解

余胜斌

(阳光学院基础教研部，福建福州 350015)

0 引言

对定义在［0，+∞)上的任一有界函数{f(t)}，本研究恒设:

主要讨论如下非自治连续型竞争系统的动力学行为:

其中:x1，x2分别表示两竞争种群在t时刻的种群密度;ri(i=1，2)表示两种群的内禀增长率;ai(i=1，2)为种内竞争系数;bi(i=1，2)为种间竞争系数;ci(i=1，2)为扰动系数.

文献［1］中首次提出系统(1)所对应的自治系统，文献［2］在文献［1］所提的系统里加入了时滞项.文献［3］进一步分析得到了系统(1)所对应的差分竞争系统的持久性、正周期解的存在性和全局渐近稳定性的充分条件.文献［4－5］则探讨了系统(1)所对应的差分系统在时滞和反馈控制影响下的持久性、正概周期解的存在性和全局吸引性.众所周知，连续型模型能很好地描述生命长，世代重叠且数量较大的种群的发展，但是已有的关于系统(1)及其相应系统的研究结果较少涉及到非自治连续型情形，因此非常有必要对系统(1)加以研究.本研究旨在得到保证系统(1)永久持续生存、全局吸引和存在唯一概周期正解的充分性判据，类似的工作参见文献［6－11］.

基于生物学角度考虑，本研究恒设系统(1)的各系数ri，ai，bi，ci(i=1，2)均为［0，+∞)上的有正上下界的连续函数，且系统(1)满足初始条件:x1(0)＞0，x2(0)＞0.从而易知对于任意的t≥0都有x1(t) ＞ 0，x2(t) ＞ 0.

1 一般非自治系统

本节将研究系统(1)的有界性，永久持续生存性和全局吸引性.为此，先给出一个引理:

引理1［12］设a＞0，b＞0，当t≥0且x(0)＞0时，若有则设时，若有则

定理1假设

成立，系统(1)是永久持续生存的即存在正常数mi和Mi(i=1，2)，使得对系统(1)的任一正解(x1(t)，x2(t))T均有

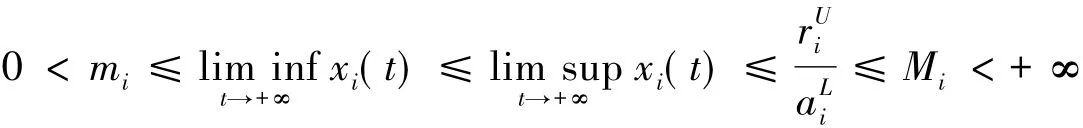
证明 由条件(H1)，存在足够小的ε＞0，使得

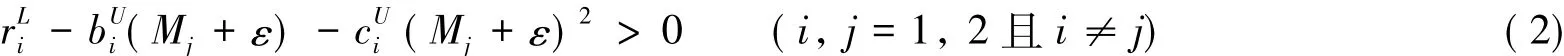
由系统(1)可得

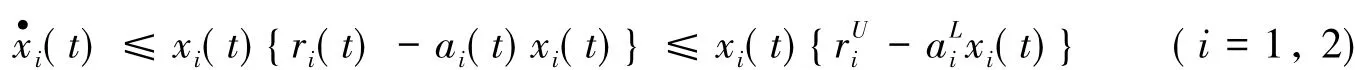
由引理1可知，

从而对上述ε，存在T1＞0使得对任意t＞T1有

由式(4)及系统(1)可知，当t＞T1时，有

由式(2)、(5)及引理1得

上式中取ε→0得

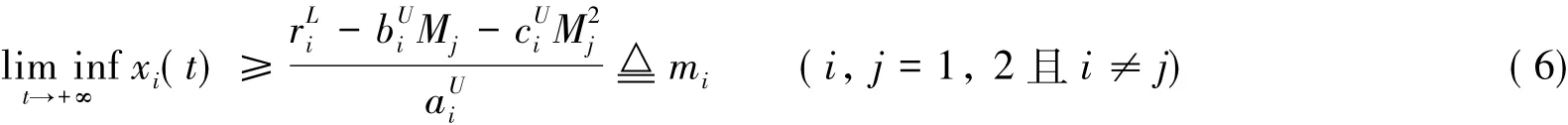
由式(3)和(6)可知，系统(1)是永久持续生存的.证毕.

定理2假设(H1)成立，进一步假设-αi＞0使得

成立，这里Mi(i=1，2)如定理1所定义，则系统(1)是全局吸引的.

证明 设(x1(t)，x2(t))T和(y1(t)，y2(t))T为系统(1)的任意两个正解.由定理1和条件(H2)可知，对任意ε＞0，存在T＞0使得对任意t＞T，有

定义Lyapunov函数

计算V(t)沿着系统(1)的正解的右上导数得

从而由式子(7)可知，当t＞T时，有

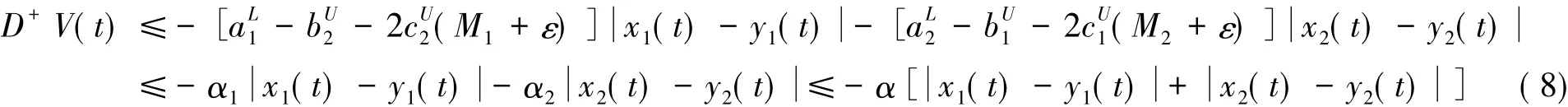
这里α=min{α1，α2}.对上式从T到t积分得:

因此，

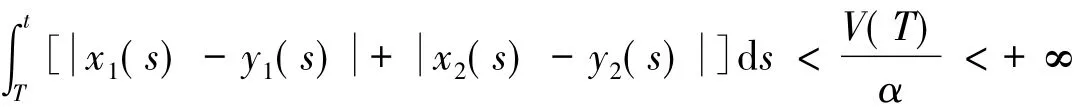
从而有

此外，x1(t)，y1(t)，x2(t)和y2(t)的最终有界性隐含了当t≥T时，x1(t)，y1(t)，x2(t)和y2(t)具有有界的导数(由其所满足的方程可知).这表明上一致连续.从而由 Barbǎlat引理［13］得

即系统(1)是全局吸引的.证毕.

2 概周期系统

由于概周期现象在生态学中更具有现实意义，因此本节中在恒设系统(1)的各系数ri，ai，bi，ci(i=1，2)均为［0，+∞)上的有正上下界的概周期函数的前提下，来进一步研究系统(1)的概周期解的存在唯一性.

考虑如下概周期系统:

及其伴随系统:

引理2［14］设D是的一个开集，函数V(t，x，y)定义在上，满足:其中a(r)和b(r)为连续、递增的正定函数.是一常数.这里λ为一正常数.

此外，设式(9)对t≥t0≥0有解位于紧集K中，KD，则式(9)在D中有唯一一致渐近稳定的概周期解.

定理3若有(H1)和(H2)成立，则系统(1)存在唯一全局吸引的概周期正解.

证明 由定理1可知系统(1)是永久持续生存的，且集合

就是持续生存域，显然K是紧集.考虑系统(1)的伴随系统:

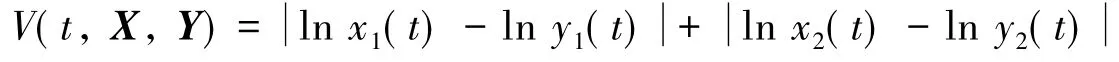
则由微分中值定理可得

从而引理2的条件(ii)成立.并对式(8)取ε→0得

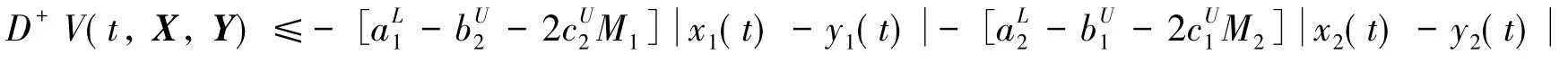
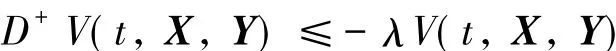
从而(iii)也成立.

由引理2可知，系统(1)在K中有唯一一致渐近稳定的概周期解.再由定理2得，该唯一的概周期解是全局吸引的.证毕.

3 应用举例

例1考虑如下系统:

对系统(12)来说，经简单计算可得 M1=M2=0.5.取 α1=0.8，α2=1，则有

从而条件(H1)和(H2)成立，则由定理3可知系统(12)存在唯一全局吸引的概周期正解，数值模拟(图1)也支持本研究的结果.

图 1 具初始条件(0.1，0.3)T，(0.2，0.4)T，(0.5，0.2)T 和(0.3，0.3)T 的系统(12)的数值模拟Fig.1 Dynamics of system(12)with different initial values(0.1，0.3)T，(0.2，0.4)T，(0.5，0.2)T，(0.3，0.3)T