共同前沿和三阶段数据包络的中国建筑业效率评价
2019-07-09陈德义王应明
陈德义,王应明
(福州大学经济与管理学院,福建福州 350108)
0 引言
建筑业作为我国重要的经济支柱,其效率水平高低直接影响到国民经济发展的速度和质量[1-2].目前,很少有学者对我国四大所有制(国有、集体、股份制、私营)建筑业效率进行探索.因此,探寻四大所有制建筑业生产效率的测算方法,找出建筑业效率低下的成因,可为其在市场经济环境下持续保持竞争力提供参考依据.
在建筑业实证研究方面,目前国内外学者主要运用以下几种模型对建筑业做实证研究:一是传统的CCR、BCC 等一阶段模型[3-6]; 二是两阶段数据包络分析(data envelopment analysis,DEA)模型[7-8]; 三是非期望产出交叉效率DEA模型[9-10];四是剔除掉外部环境和随机误差的三阶段DEA模型[11-14].
在模型方面,由于在实证中存在外部环境与随机误差等因素对效率计算的影响,文献[15]提出了三阶段DEA模型,其中在第二阶段以投入松弛为因变量、外部环境因素为自变量建立成本导向的随机前沿分析(stochastic frontier analysis,SFA)模型,进而剔除掉外部环境因素的影响.但是文献[15]没有给出管理无效率的公式,只是说明可以参考文献[16]提出的公式,而其公式用的是生产函数,不能用于该文中管理无效率的测算.国内部分文章均为基于生产函数的角度给出管理无效率分离公式[17-18].文献[19]提出了统一分布假设的三阶段DEA模型管理无效率的估计公式也是基于生产函数得出的.文献[20]在其基础上应用JLMS方法并根据成本函数的思路推导出成本函数角度的三阶段DEA模型管理无效率的估计公式.
但在实证过程中发现三阶段DEA模型也存在某些不足处.比如对一些原投入调整之后发现新投入是原来的几倍甚至几十倍;在参照集的选择方面,传统三阶段DEA模型选择以最差的环境和随机误差为参照集,但是在现实社会中以最差的对象作为参考来评价其他决策单元的效率是不合适的,也没有实际意义.鉴于此,首先,提出一种改进调整模型,克服调整之后某些新投入与原投入相差巨大,得出的效率值可比性不强的缺陷;然后,找出新的参考集,使其实现参考价值;最后,把三层级共同前沿DEA模型与改进的调整模型结合,分析近几年来四大所有制建筑业的效率.
1 三阶段DEA改进模型的构建
1.1 第二阶段调整公式
第二阶段运用SFA的随机成本模型进行回归分析,其表达式如下:

其中:n=1,2,…,N表示n个投入;i=1,2,…,I表示i个决策单元;Sni为第i个决策单元在第n个投入上的松弛变量;fn(Zi;βn)为外部环境因素对松弛变量的影响;Zi为环境变量;βn为环境变量的系数,Vni+Uni为混合误差项;Vni表示随机误差项,呈正太分布,Uni表示管理无效率,并服从在零点截断的单边正太分布.Vni与Vni独立不相关.
关于管理无效率的分离公式,目前均采用成本函数形式下管理无效率的估计公式:
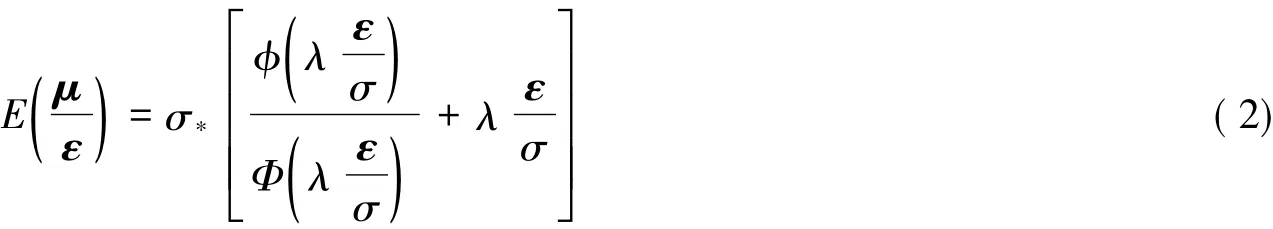
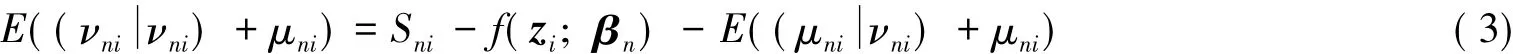
而SFA回归的目的是剔除环境因素和随机因素对效率测度的影响,以便将所有决策单元调整于相同的外部环境中.调整公式如下:

1.2 三阶段DEA模型存在的问题
问题一:调整后部分新值比原值大很多.
在调整投入的时候会发生一个现象,在前沿面上的决策单元的投入在调整之后变为原值的几倍甚至几十倍,这样的结果显然是不正确的.以下运用数学模型证明传统三阶段DEA模型存在的问题:
由公式(1)可得:

则由公式(4)可得:
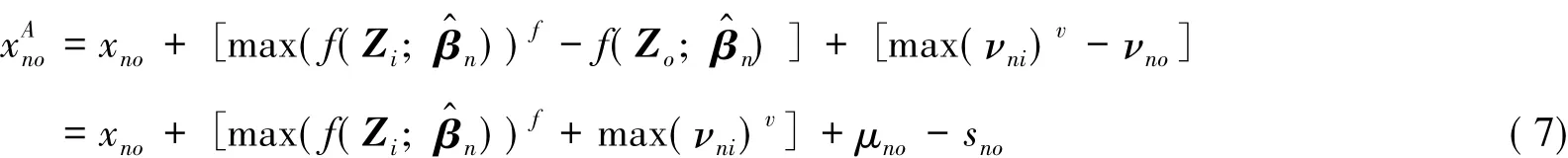
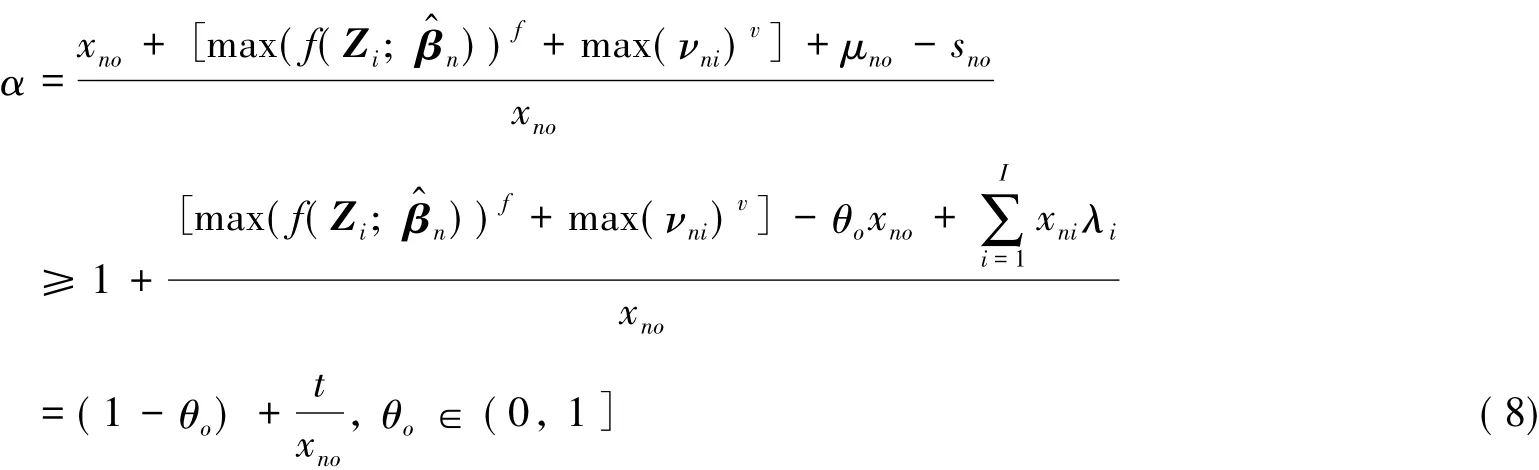
1)当xno远小于t时,无论θo的值为多少,α值都将变得很大,调整之后的新投入xAni远大于原投入,因此原有的调整公式变得不合理.具体来说,假设有一个决策单元处在生产前沿面上,但是投入比较小,而其所处的外部环境比较好,因此t值会比较大,甚至远大于原投入xno,使得新投入xAno远大于原投入xno.
2) 当 xno远大于时,

① 当θo=1时,此时松弛变量sno为0,xno在生产前沿面上,此时对投入进行调整不会有任何变化.
② 当θo→0时,此时xno远离生产前沿面,则此时对投入进行调整也不会产生变化.
③ 当θo∈(0,1)时,α∈(0,2),对投入进行调整不会出现新投入比原投入大很多倍的情况,此结果比较符合实际.
3)当t∈(0,+∞)时,α∈(0,+∞),此结果不符合实际.
综上所述,若要使调整公式 (4)成立,则必须满足充分条件:xno远大于max(νni)v].然而和max(νni)v与θo和xno无关联,投入并不一定能满足上述充分条件,存在局限性.所以,原有三阶段DEA模型中的关键模型不适用于投入或产出的调整,需寻找方法建立新的调整公式.
问题二:参照集选取不合理.
在参照集选择方面,传统三阶段模型选择以最差环境和随机误差为参照集,但是在现实社会中以最差对象作为参考来评价其他决策单元的效率是不合适的,也没有实际意义,其中带有些许“歧视”的味道.
1.3 基于共同前沿的三阶段DEA改进模型
第一阶段:三层级共同前沿DEA模型.
为了计算不同体制、不同区域建筑业企业的效率值,本阶段借鉴文献[21]中提出的共同前沿DEA模型,将该模型运用到四大所有制建筑业效率测算当中,同时,将其引入三阶段DEA模型中.本研究在充分考虑所有制结构和区域间存在技术差距这一现实的前提条件下,假定四大所有制建筑业企业存在所有制结构技术以及区域技术并具有异质性,构建了生产共同前沿、所有制分组前沿和区域分组前沿.
本研究将生产共同前沿、所有制分组前沿以及区域分组前沿下的建筑业企业效率分别表示为βc、βo、βr.而不同所有制建筑业企业在不同区域有着不同的所有制属性优势、技术水平和管理水平.其中,βc、βo、βr可以通过以下DEA模型得出:
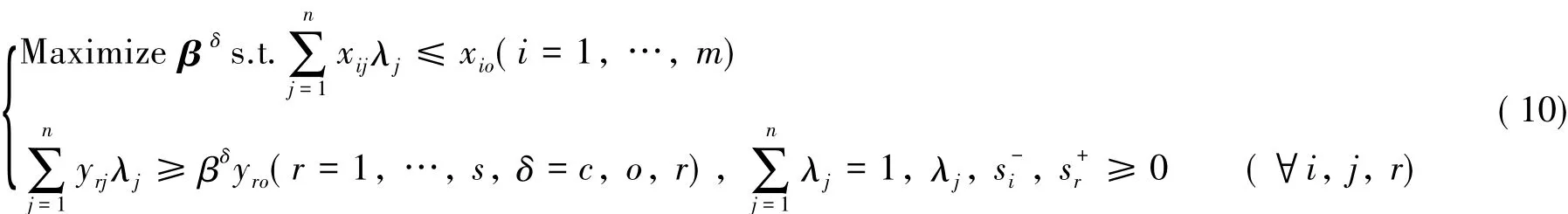
第二阶段:改进调整式.
本研究在综合分析并证明了传统三阶段DEA第二阶段的不足后,发现以加法的形式对原投入或产出值做调整显然是不合理的.综合上述情况,外部环境因素应是对“框架”中的投入、产出值产生一定程度的促进或者抑制作用.所以,通过调整并引入环境乘数的概念,针对外部环境指标数值是确定的情况,提出如下调整公式:
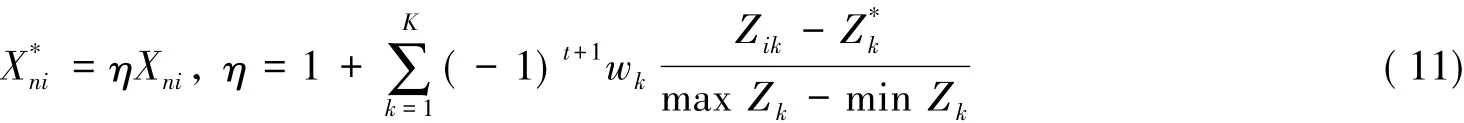
这里t=0(t=1),对松弛变量进行SFA分析时,环境变量系数为正(负).其中:η为环境乘数;wk为环境变量的权重;Zik为第i个决策单元第k个环境指标的环境值;为第k个环境指标的参考值;Xni为第i个决策单元第n个投入的原投入值;为第i个决策单元第n个投入的新投入值.该调整公式是否合理,能不能解决原调整模型中存在的问题,需要被证明,证明如下:
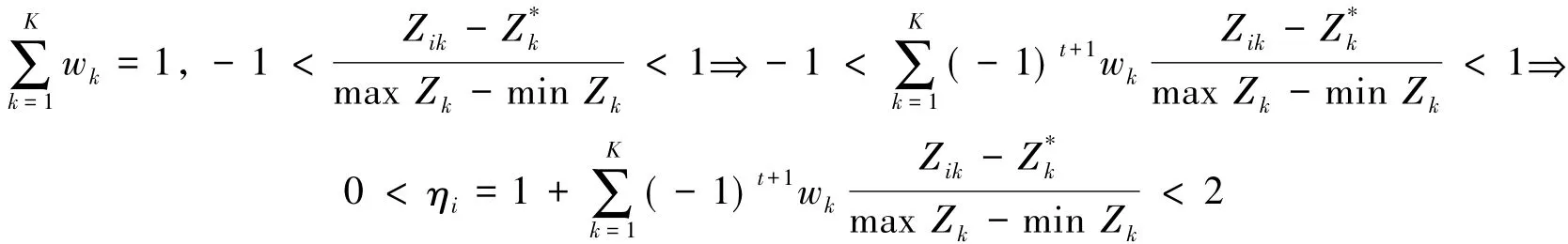
环境乘数的取值范围在0到2之间,运用该调整模型对投入进行调整之后,不会出现新投入远大于或远小于原投入的情况,因此,该环境乘数是合理的,调整公式也是合理的.由于篇幅有限,本研究仅针对外部环境指标数值是确定的情况构造改进的三阶段DEA模型,在指标数值是确定的条件下运用熵权法[22]求环境变量权重 wk.
在现实生活中,在选取指标参考点时是不会以指标中最差的点作为参照来显示本身的优越性,也不会选取指标中最优的点来显示本身有多“差劲”.基于此思想,选取各个环境指标的均值作为参照应更合理.因此本研究选取均值作为参照集:

第三阶段:调整之后重新进行DEA分析.
运用新调整公式得到新的投入值,产出值不变,导入第一阶段重新进行效率测算,得到剔除掉外部环境因素影响的效率值.
2 评价指标的选取与数据来源
2.1 投入产出指标选取
参考并梳理已有的相关文献[7-8,12],在投入指标的选取上主要包括从事建筑业活动的平均人数、建筑业总资产、自有机械设备年末总功率、能源利用率等指标.鉴于在《中国建筑业统计年鉴》和国家统计局中,四大所有制建筑业的“自有机械设备年末总功率”指标绝大多数无法获取,通过参考比较相关文献[2-7],选取从事建筑业活动的平均人数和建筑业总资产作为投入指标.
2.2 环境指标的选取
环境指标应该选取对建筑业效率产生影响但是又不在样本主观可控范围的因素.综合分析大量的相关建筑业效率方面的文献[11-14],并考虑到目前数据的完整性,选取产业发达程度、地区经济发展水平、市场化水平和投资水平四个指标作为影响建筑业企业产能效率的外部环境因素.
3 我国四大主要所有制建筑业效率测度及其分析
3.1 第一阶段:共同前沿DEA模型的实证结果
模型实证结果见图1.由图1可以看出,在不考虑外部环境的情况下,通过加权平均所有制分组前沿下的不同省份的建筑业企业效率,国有、集体、私营、股份制建筑业企业2007—2015年的效率呈现出很大的差异,且产能过剩现象严重.数据显示,2007—2015年以来四大所有制建筑业企业的效率都低于0.9,效率低下,2007年股份制建筑业企业效率平均值仅为0.8,处于最低的效率水平.而我国建筑业企业效率低下主要是由于股份制建筑业企业低下导致的,不过其整体效率呈现出逐步上升的趋势.在2007—2010年,集体和私营两种所有制的走势大致相同,呈逐步上升的趋势,但在2011年私营制建筑业企业效率值大幅度下滑到0.85以下,2012年回暖之后,在2015年又大幅度下滑到0.809.国有建筑业企业在2011年前与其他三个呈相反的趋势,2011年之后效率值逐步上升.
3.2 第二阶段:随机前沿分析结果
将第一阶段各投入变量的松弛变量设为被解释变量,外部环境因素设为解释变量,应用Frontier 4.1软件分别对两个投入指标进行SFA回归,回归结果如表1所示.

表1 第二阶段SFA回归结果Tab.1 SFA regression results
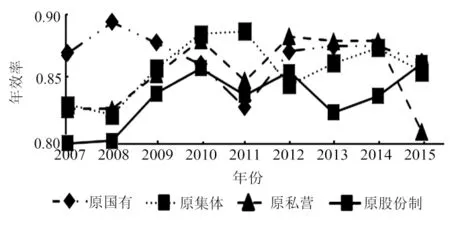
图1 基于共同前沿模型实证建筑企业效率Fig.1 Empirical study on construction industry efficiency based on meta-frontier model
回归结果表明,各外部环境变量对两个投入松弛变量的回归系数都在1%的显著性水平上通过检验,表明外部环境因素在一定程度上对投入变量产生影响,而产业发达程度、地区经济发展水平、投资水平的系数都为负,说明这三个环境变量能减少投入松弛,对投入变量有一定程度的正向影响作用.市场化水平系数为正,则该环境指标在一定范围内增加投入松弛,从而对投入变量有一定程度的负向影响作用.
3.3 第三阶段:基于共同前沿三阶段DEA改进模型的实证结果
改进模型的实证结果见图2.由图2可知,在最大值和最小值上,新的效率值比原效率值均大了2个百分点左右,2007年四大所有制建筑业效率值都处于0.87以上,明显高于原效率值.而导致我国建筑业企业效率低下的主要原因是国有和集体建筑业企业效率低下,而不是由股份制建筑业企业效率低下导致的.在2008年,为了应对金融危机,政府投入“4万亿”刺激消费,国有建筑业效率值在当年有所上升,之后由于过度的浪费导致效率持续下降,到2011年才开始缓慢上升.集体制建筑业效率值在2008年到达最低点0.853,在2009年上升到0.892之后又开始走下坡路.2007—2012年私营制和股份制建筑业企业整体走势大致相同,在2012—2015年,国有、集体、私营制建筑业企业走势也相同,持续下跌.在2013—2015年股份制建筑业企业效率持续上升,在2015年反超其他所有制建筑业,效率值达到0.907,处于领先地位.
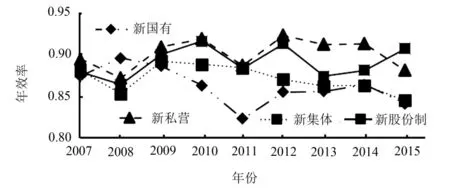
图2 基于改进的三阶段DEA模型实证建筑企业效率Fig.2 Empirical study on construction industry efficiency based on the improved three-stage DEA model
在考虑外部环境因素影响的情况下,通过加权所有制分组前沿下不同省份四种所有制建筑业企业数据,可计算得出东、中、西部区域的效率(见图3).从总体上看,东部地区建筑业企业效率大于中西部地区,中部地区又大于西部地区,表明建筑业企业呈现明显的区域差异.在2007—2015年四种所有制建筑业企业平均效率为0.882,其中东部地区为 0.899,中部地区为 0.886,而西部地区最小,仅有 0.859.从趋势上看,东部和中部地区建筑业企业效率整体呈下降趋势,且变化趋势基本一致,而西部地区整体呈上升趋势.具体来说,东部地区效率值一直处于领先地位,在2007—2010年间效率基本保持在0.915水平;而在2011年东部和中部地区大幅度下降2~4个百分点,在2012年又大幅度上升2~4个百分点,在2012年之后又逐年下降,到2015年达到最低点.西部地区总体效率较低,在2008年效率达到最低值0.83,但整体效率呈现上升趋势,有一定的潜力,并在2015年超越东部和中部,效率值达到0.883.
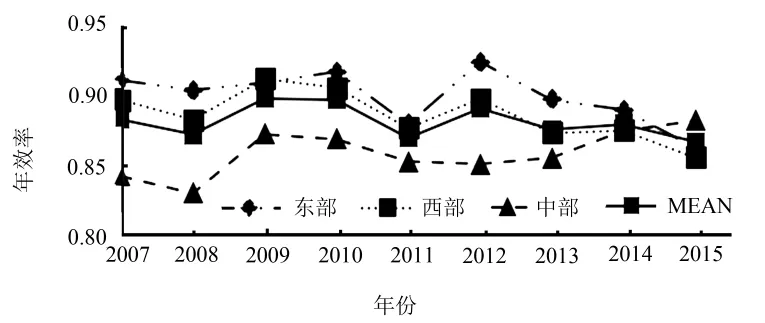
图3 我国东、中、西部建筑业企业效率Fig.3 Efficiency of China’s construction enterprises in eastern,central and western area
4 结论
1)建筑业企业效率整体偏低,技术、管理、所有制结构都没达到理想水平.因此,当前建筑业企业需要响应“十三五”发展规划的号召,调整优化产业结构,推进以BIM为核心的信息化技术的开发应用,鼓励以技术专长、制造装配一体化、工序工种为基础的专业分包,促进小微专业企业发展.同时支持“互联网+”模式整合资源,联通供需,降低成本.
2)对于国有建筑业企业要加大其在中西部技术水平的投入,引进高技术人才,优化产业结构;集体建筑业企业在中部地区需要加大技术投入,在东部需要调整产业结构;东西部地区的私营建筑业企业同样也需要调整优化其产业结构.
3)对于西部地区,国有和私营企业需要引入技术和人才,健全技能培训和鉴定体系,推动工人组织化和专业化.同时,西部地区需要加大市场开拓力度,加大对外开放水平,充分把握“一带一路”战略契机,发挥我国建筑业企业在高速铁路、公路、电力、港口、机场、油气长输管道、高层建筑等工程建设方面的优势.
4)对于东部地区,特别是集体、私营、股份制建筑业企业,国家需要注意政策资源的适度均衡配置,避免优惠政策的过度供给和叠加供给.
