两点边值问题网格方程病态机理和预处理

张 衡，郑汉垣

(1.福建师范大学福清分校，无损检测技术福建省高等学校重点实验室，福建福清 350300;2.福建师范大学福清分校电子与信息工程学院，福建福清 350300;3.龙岩学院传播与设计学院，福建龙岩 364012)

0 引言

两点边值问题大规模数值求解问题，是使用不同的离散方法转化为各种网格方程来求解的，这些网格方程的病态(高条件数)随着问题规模的增加而增加［1］，成为制约求解效率和精度的瓶颈因素.因此，在求解之前，使用预处理方法来减少方程组的病态，成为提高求解效率和精度的必要措施.

所谓“预处理方法”是指在求解方程组

并保证不增加大的计算成本的前提下，用线性变换将方程组(1)转化成等价的方程组

使得Cond(A')＜＜Cond(A)，其中线性变换矩阵称为预条件子［2－3］;如果Cond(A')与A的阶数无关，则称预条件子为最优预条件子［4］.

病态方程组的成功求解，依赖于适当的预条件子.然而，由于缺乏对病态机理和预处理原理的研究，目前关于预处理问题的理论和研究方法都不完善，一是缺乏一般的预处理方法，以及最优且通用的预条件子，通常是针对具体问题，根据预条件子的基本要求，设计具体的预条件子［5－7］.二是对预处理的效果(条件数下降的程度、条件数的估计、对计算量的影响等)缺少科学的定量分析，多用定性分析和实验结果说明［8－14］.

本研究讨论病态机理和预处理原理.定义方程组的病态结构、病态因子、去病因子，并讨论其性质和作用.目前关于病态机理和预处理原理的研究鲜见有成果发表.

求解两点边值问题时，使用有限元方法和有限差分方法形成不同的网格方程.基于结构分析的思想［15－18］，本研究对网格方程的病态机理和预处理原理进行探讨.研究结果说明，这些不同的网格方程有类似的病态结构和相同的病态因子以及对应的去病因子;将病态分为由病态因子表达的原发病态和由具体问题引起的继发病态，更准确地说明了不同的因素对病态的影响;推广文献［17－18］的方法，依次针对原发病态和继发病态进行了二次预处理，通过定量分析预处理的效果(条件数下降的程度，对计算量的影响)，说明了在几乎不增加计算量的情况下，预处理后的条件数接近1;通过与文献［17－18］的比较，说明了去病因子不仅是网格方程的最优预条件子［4］，而且作为预条件子主要部分，具有通用性.

1 矩阵的病态结构

1.1 矩阵的病态结构

定义1矩阵A的如下结构称为病态结构:

1.2 去病因子

命题11)如果Z∈Rα×β，β≥α，ZZT可逆，则对任意β阶正定对称矩阵P，有

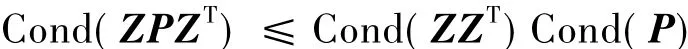
2)如果可逆矩阵H满足ZZT=HHT，则对任意β阶正定对称矩阵P，有

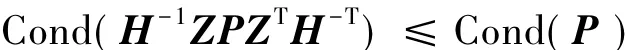
证明 1)利用Rayleigh－Ritz定理［19］，有

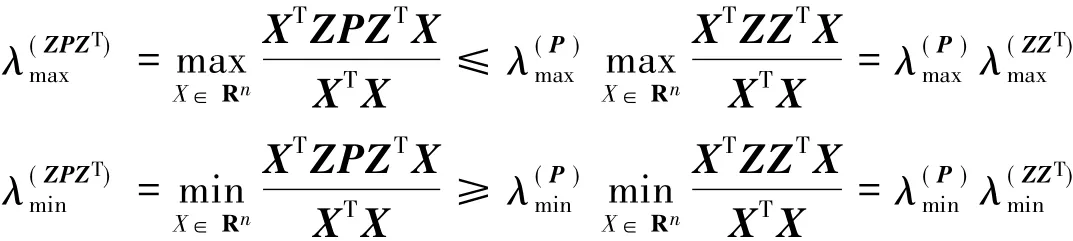
2) 根据结论 1)，有 Cond(H－1ZPZTH－T) ≤ Cond(P)Cond(H－1ZZTH－T)，由 ZZT=HHT，有Cond(H－1ZZTH－T)=1，所以结论成立.证毕.

定义2如果Z∈Rα×β，β≥α，ZZT可逆，则称满足ZZT=HHT的可逆矩阵H为属于Z的去病因子.

若病态矩阵A病态结构中，病态主体ZPZT是正定对称的， ZPZT＞＞ Q ，Z，ZT是病态因子，可逆矩阵H为属于Z的去病因子，则根据命题1结论2)，A≈ZPZT，Cond(H－1AH－T)≈Cond(H－1ZPZTH－T)≤Cond(P).上述分析说明去病因子H可以将病态主体的条件数降为P条件数，相当于消除了病态因子的作用.

1.3 特殊的病态因子和去病因子及其性质

为方便起见，记In为n阶单位矩阵，0n为n维零向量的第i个列向量则可以直接验证得到下面的命题2～3.

命题2［20］

命题3任意n阶对称矩阵B=(bi，j)n都可以写成其中:

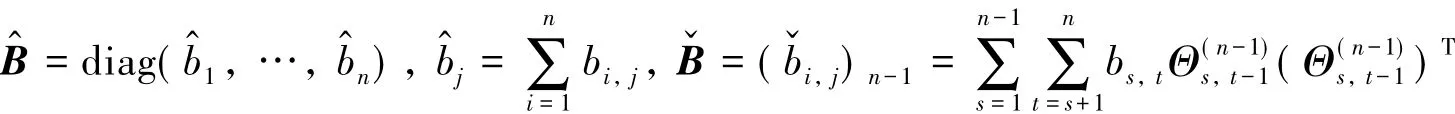
命题2说明，Un是病态因子，Ln是Un的去病因子.

2 两点边值问题网格方程的病态结构

2.1 两点边值问题Lagrange有限元方程的病态结构

使用有限元方法，求解积分形式的两点边值问题［21］

将［a，b］剖分成m+1个小区间，每个小区间内k－1个信息点，取k次Lagrange形函数，则根据问题(4)的有限元离散格式［21］，得到问题(4)的有限元方程［16］

其中:P是m阶块对角矩阵，第i个块Pi=(p(s，i)t)k是k阶正定对称矩阵;Q是对角矩阵; P ＞＞ Q ，Z=k=2时为文献［17］的情形，k=3时为文献［18］的情形.根据命题1～2和定义1可知，式(5)表达了A的病态结构，ZPZT是A的病态主体，Z，ZT分别是A的左、右病态因子，H=Ln为方程(5)中Z的去病因子.

2.2 两点边值问题有限差分方程的病态结构

使用有限差分方法，求解两点边值问题［21］

得到差分格式

根据差分格式(7)，易得到下列命题4

命题4问题(6)有如下的差分方程

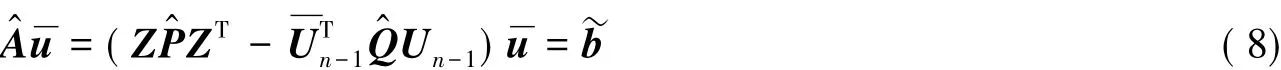
3 两点边值问题网格方程的病态机理与去病因子

在方程(5)、(8)中，病态结构类似，有相同的病态因子以及对应的去病因子.ZPZT，ZP^ZT是网格方程的病态主体对网格方程的病态影响很小.

定义3称病态因子Z表达的病态为原发病态表达的病态为继发病态.

4 网格方程的预处理及其效果分析

仅讨论方程(5)的预条件子，k=1时即为方程(8)的预条件子，方程(8)中相当于方程(5)的的不对称性，不影响预处理过程与效果.根据命题3，易验证下列命题5.

命题5对于式(5)，有其中:是m阶块对角矩阵，第i个块分别记为ˇ

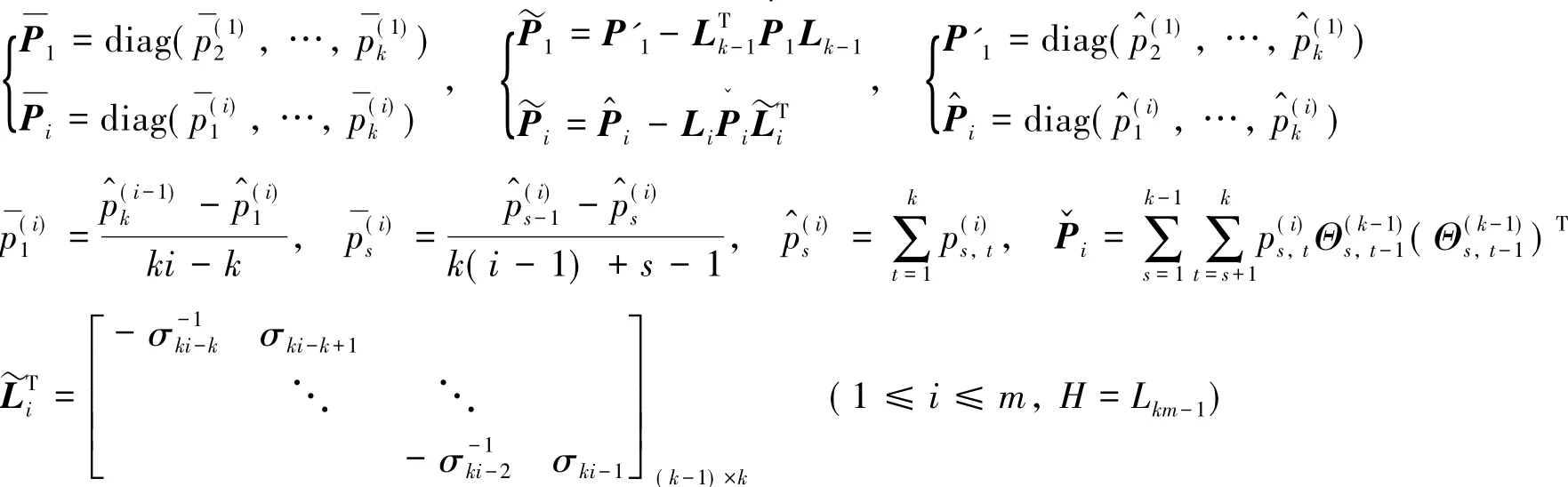
上述预处理方法是文献［17－18］方法的推广.k=1时即为方程(8)的情形，k=2时为文献［17］的方法，k=3时为文献［18］的方法.对于方程(10)，可以取迭代式为u″(k+1)=d″－Ru″(k)，在该式的求解中，无需计算R，每个迭代步，只要一次R与向量的乘积计算，O(kn)次计算操作，与一般的迭代法相当.方程(9)～(10)的系数矩阵主体仍然是正定对称矩阵，可以使用经典Krylov子空间方法——共轭梯度法求解，即为预处理共轭梯度法［2］，其中主要的计算操作仍然是R与向量的乘积，所以计算量几乎没有增加.

5 结论

基于结构分析的策略，研究两点边值问题网格方程的病态机理和预处理原理，结论如下:

1)对于不同两点边值问题，使用不同的离散方法形成不同的网格方程.这些网格方程隐藏着类似的病态结构和相同的病态因子，病态因子表达了主要的病态——原发病态，而次要的病态——继发病态则因具体问题、具体方法的不同而不同，针对病态因子，可以找到去病因子，使用去病因子作为预条件子的重要部分，可消除病态因子的作用，即消除原发病态.

2)文献［17－18］中的网格方程，与本研究两种网格方程有相同的病态因子，因此相应的去病因子也相同，这说明作为预条件子主要部分的去病因子，是预条件子中可以通用的部分.

3)使用去病因子进行预处理后，网格方程的条件数，几乎与网格方程的阶数无关，因此去病因子是最优预条件子［4］.

4)使用去病因子进行预处理，不明显增加计算成本，也不改变网格方程的正定对称性.

综上所述，通过结构分析，发现病态结构和病态因子，确定原发病态和继发病态，有针对性地设计出最优的、通用的预条件子，可以有效地解决病态问题.