基于包络仿真的谐波齿轮刚轮设计方法
2019-07-09张开元汪中厚
张开元, 汪中厚
(上海理工大学 机械工程学院, 上海 200093)
谐波齿轮是依靠柔轮的周期性弹性变形实现传动的新型传动机构,谐波齿轮具有结构紧凑、体积小、传动精度高、传动比大以及同时啮合齿数多等特点,因而得到了广泛应用和研究[1]。在机器人关节和伺服系统中,使用谐波齿轮减速器替换传统齿轮减速器可以极大地提高定位精度和响应灵敏度[2-3]。
谐波齿轮传动机构主要由三个零件组成:波发生器、柔轮和刚轮。其中,波发生器根据工况的需要可以进行调整和互换,柔轮齿廓的求解是按照设计要求的齿形,分别计算齿廓参数得到的[4]。
目前,谐波齿轮刚轮的设计是通过设计公式进行计算,实际加工后再根据啮合效果对参数进行调整来实现的[5]。刚轮与柔轮在设计过程中保持了相对的独立,刚轮的齿廓往往和柔轮齿廓配合效果不佳,导致传动机构精度降低。
另一方面,谐波齿轮在进行有限元分析之前,需要对传动机构进行三维建模。现有的建模手段构建三维模型时过于繁琐,为了解决上述问题,已经有学者尝试使用参数化建模的方法提高谐波齿轮设计效率[6-7]。然而,参数化建模只能缩短标准渐开线齿形的设计时间,当与柔轮配合的刚轮齿廓为非标准渐开线齿廓,或是使用了双圆弧、摆线等特殊齿廓时,参数化建模方法在灵活性和通用性方面存在的问题就会暴露出来。
因此,本文以谐波齿轮共轭理论为依据,分析实际传动中柔轮的运动轨迹,在MATLAB中通过编程实现柔轮运动仿真,在双圆弧柔轮齿廓设计的基础上,进行不同径向变形系数的包络仿真,分析径向变形系数对共轭齿廓的设计影响。
1 谐波齿轮共轭理论
在进行刚轮共轭齿廓求解时,把柔轮的齿廓假想成刀具的轮廓,刀具在波发生器的激励下,形成特定的运动轨迹[8]。在这一过程中,柔轮所占据的位置,都视为被假想刀具切削掉,所形成的包络线簇即为所需的刚轮共轭齿廓。
柔轮设计坐标系以柔轮中性面作为横坐标轴,以波发生器长轴作为纵坐标轴。刚轮设计坐标系以波发生器短轴作为横坐标轴,以波发生器长轴作为纵坐标轴。刚轮和柔轮的设计坐标系并不相同,坐标系的位置关系如图1所示。

图1 齿廓设计坐标系位置关系
柔轮在装入波发生器后,内圈从圆形拉伸为椭圆形。距离柔轮内圈长轴处t/2距离处的平面为柔轮的中性面,柔轮是在坐标系xRORyR中设计的,该坐标系以柔轮中性面为横坐标轴xR,以齿廓对称线作为纵坐标轴yR。在进行刚轮设计时,考虑到柔轮需要围绕回转中心旋转和径向位移,因此需要将柔轮的坐标转换到刚轮坐标系中。刚轮坐标系以波发生器的回转中心OG作为原点,波发生器长轴作为横坐标轴xG,波发生器短轴作为纵坐标轴yG。
谐波齿轮以固定刚轮、波发生器主动,柔轮从动的形式传动时。柔轮的空间位置发生变化,对应在刚轮坐标系中坐标变换矩阵为
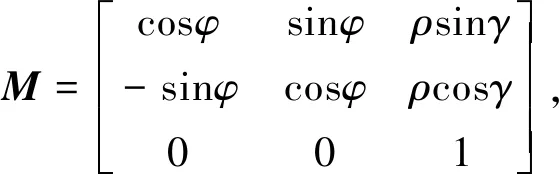
(1)
式中φ为柔轮位置变化后两坐标系纵坐标轴之间的夹角,ρ为柔轮变形后的向径,γ为波发生器和刚轮转角差值。根据谐波齿轮第一定律,柔轮与刚轮之间可以视作是无滑动的纯滚动运动,柔轮运动的弧长应等于刚轮运动的弧长,即
(2)
式中φ1为柔轮位移圆弧对应的角度,φ2为刚轮位移圆弧对应的角度,rG为刚轮特征曲线半径。进而按照γ的定义,可以求出
(3)
计算出位移圆弧夹角γ后,可以得到
(4)
因此,共轭齿廓参数方程组可以表示为
(5)
2 仿真求解刚轮共轭齿廓
在MATLAB中进行包络仿真可以快速求解出刚轮共轭齿廓,进行编程之前,首先要对柔轮的运动轨迹进行分析。柔轮在传动过程中的运动属于复合运动,可以拆解为径向运动和切向运动。波发生器转过角度α后,柔轮转过角度β,柔轮的运动轨迹如图2所示。

图2 柔轮运动轨迹

图3 包络仿真程序框架
柔轮的运动过程可以分解为从A点沿着特征曲线运动到B点,再沿着椭圆向径从B点运动到C点。
谐波齿轮的波发生器为椭圆形,当波发生器转过90°时,波发生器长轴处的柔轮完成从啮合到啮出的过程。谐波齿轮的传动比很大,这里用于包络仿真的传动机构传动比为100。在该传动比下,波发生器转过90°,对应柔轮从动转过0.9°,转过的角度很小。切向运动走过的圆弧可以近似视为一段以柔轮向径ρ作为半径的圆弧,切向运动的弧长Δx可以表示为
(6)
在径向方向上,波发生器向径的变化量即为柔轮齿廓沿径向的位移,径向运动量Δy可以表示为
(7)
式中a为波发生器长轴长,b为波发生器短轴长。
根据上述分析,在MATLAB中进行包络仿真求解刚轮共轭齿廓的程序基本框架如图3所示。
3刚轮齿廓求解结果
谐波齿轮第二定律认为:刚轮的共轭齿廓与柔轮齿廓的截形和波发生器的尺寸有关。在确定了柔轮齿廓后,刚轮齿廓的求解就仅受波发生器尺寸的影响。
波发生器的尺寸是通过影响柔轮的径向变形系数ω*来改变啮合过程的,ω*可以由下式确定:
(8)
其中m为柔轮模数,ω为柔轮最大径向变形量。从图1中可以看出,最大径向变形量即为波发生器长轴a和柔轮未变形前的半径r之间的差值,即:
ω=a-r。
(9)
选取ω*为1的标准传动形式进行仿真,得到的包络线簇如图4所示。在设计时,增大柔轮的径向变形系数,可以增加柔轮的啮入深度,提高传动机构的承载能力[9]。调整径向系数为1.2,得到的包络线簇如图5所示。

图4 ω*为1的柔轮包络线簇 图5 ω*为1.2的柔轮包络线簇
从图5中可以看出,在这种传动形式下,组成刚轮齿廓的线条数少于径向变形系数为1时的线条数,即柔轮和刚轮的有效啮合区间有所缩小。在啮出的过程中,柔轮齿顶和刚轮包络齿廓的齿顶之间距离明显增大,存在跳齿的可能性。
减小径向变形系数,会使得波发生器的形状更贴近于圆形,可以增加传动机构的同时啮合齿对数,补偿传动误差。柔轮在波发生器的作用下,拉伸延展比较小,有利于提高柔轮的弯曲疲劳寿命,当径向变形系数为0.8时的包络线簇如图6所示。
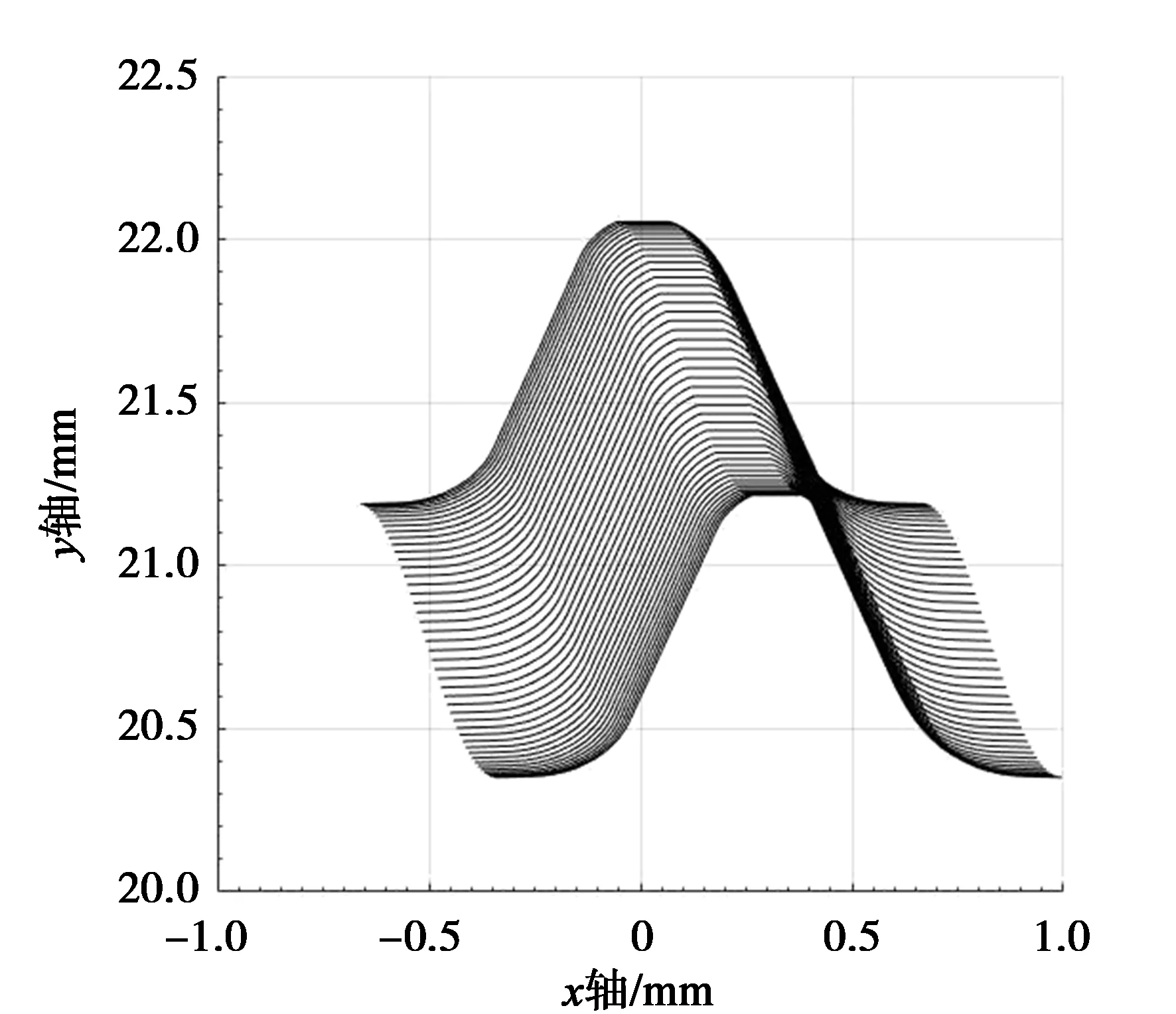
图6 ω*为0.8的柔轮包络线簇
仿真结果表明,柔轮的啮入深度有所降低,有效啮合区间明显增大。在啮出过程中,柔轮齿顶和刚轮包络齿廓齿顶之间的距离过小,这就使得刚轮和柔轮之间的啮合传动过程容易发生干涉。
综上所述,在设计刚轮共轭齿廓时,需要根据啮入深度、重合度、有效啮合区间和齿廓间隙等啮合选择合适的径向变形系数。同时,为了避免跳齿和干涉现象,径向变形系数的选择范围为0.8~1.2之间。
4 刚轮齿廓的拟合
在完成了包络仿真后,需要对包络所得的齿廓坐标进行曲线拟合,完成与柔轮配合的刚轮齿廓设计。首先要将所有的数据进行离散化,重新分割x轴,进行间隔取点。依次提取当前横坐标位置的纵坐标最大值ymax,取这组坐标作为刚轮齿廓组成点,刚轮齿廓坐标点的提取结果如图7所示。
提取全部齿廓坐标后,在MATLAB中进行数据处理,拟合出刚轮的齿廓。MATLAB中可以实现多项式拟合和加权拟合,多项式拟合是使用polyfit函数,通过最小二乘法实现曲线拟合的[10]。多项式拟合实现较为简单,但是容易出现数据震荡,因此选用加权拟合进行刚轮齿廓的曲线重构。
加权拟合不要求通过每一个数据点,通过计算坐标点到拟合曲线的垂直距离方差,为每一个坐标点进行加权,得到最贴合数据整体走势的平滑曲线。在MATLAB中进行加权拟合,得到的刚轮齿廓如图8所示。

图7 刚轮齿廓坐标点提取结果 图8 刚轮齿廓拟合结果
刚轮齿廓拟合结果可以以样条曲线的形式导入到Creo中,重构出刚轮齿面。通过镜像、阵列、实体化等处理后,能够构建出刚轮的三维模型,如图9所示。

图9 刚轮三维模型
在进行包络仿真时使用的柔轮齿廓为双圆弧齿廓,因此求得的刚轮共轭齿廓也属于双圆弧齿廓。与现有的参数化建模手段相比,包络仿真求解共轭齿廓的方法不受柔轮齿廓形状的限制,并且可以快速得到与给定柔轮配合的刚轮三维模型,在建立了CAD模型的基础上,可以进行后续的CAE分析,研究传动机构啮合的运动学和力学特性。
5 结 论
本文使用包络法进行了谐波齿轮刚轮的设计,得到了以下结论:
(1)使用MATLAB进行编程和仿真,可以极大降低共轭齿廓求解的计算量,得到柔轮包络线簇。设计方法不受齿廓形状的限制,并且在设计阶段考虑到了波发生器尺寸的影响,在求解与不同柔轮和波发生器配合的刚轮齿廓时具有灵活性。
(2)径向变形系数对于刚轮的设计影响很大,径向系数过小容易发生跳齿,反之容易出现啮合齿面的干涉。为了避免跳齿和干涉现象的出现,在设计阶段应保证径向变形系数介于0.8~1.2之间。
(3)通过加权拟合,能够生成平滑的刚轮齿廓曲线,进而重构出刚轮齿面,可以用于后续研究。
