Ti3(Ge1-xSix)C2固溶体力学和热力学性能的第一性原理研究

李亚盟, 金文媛, 焦照勇

(河南师范大学物理与材料科学学院 光电子技术及先进制造河南省工程实验室，新乡 453007)

1 引 言

三元层状化合物Mn+1AXn(n=1, 2, 3，其中M是早期过渡金属，A是第三、四主族元素，X是C或N元素)由于其具有金属材料的优点，如：良好的导电和导热性，较小的硬度和很强的抗腐蚀能力，同时还具有陶瓷材料的高比刚度，高熔点，良好的热稳定性和抗氧化性的特点，引起了人们的极大关注. 在MAX相材料中，Ti3AC2(A=Ge, Si)材料是比较有代表性的，Mane等[1]在实验上研究了MAX相Ti3GeC2固溶体粉末的合成与烧结，成功地合成了高纯Ti3GeC2粉体，对其形成反应研究发现，在锗的熔融后随着反应的缓慢扩散，开始发生液-固反应. 近些年来人们对于MAX相材料的研究主要集中在以下三个方面：一是新MAX相材料的合成；二是如何提高MAX相材料合成纯度；三是如何改善MAX相材料的性能. 其中，对MAX相材料中的M、A或X位置进行固溶掺杂是实现MAX相陶瓷材料的强化的一个有效的方法，可以在一定程度上改善MAX相材料的性能. Ganguly等[2]实验合成了Ti3GeC2和Ti3(SixGe1-x)C2固溶体并对其力学性质进行了分析，发现Ge含量增加会导致抗压性下降. 目前人们对于三元层状陶瓷Ti3AC2材料的研究主要集中在研究纯相材料的电子结构和力学性能，如胡洁琼等[3]采用第一性原理研究了Ti3AC3相(A = Si, Sn, Al, Ge)的电子结构、弹性性质，并且对几种MAX相材料的性质进行了比较. Cui等[4]采用第一性原理计算方法研究了压强对Ti3GeC2结构稳定性的影响.而关于Ti3(Ge1-xSix)C2固溶体的晶体结构、结构稳定性、力学以及热力学性能的系统理论研究鲜见报道. 基于此，本文将采用基于密度泛函理论(DFT)的第一性原理计算方法对Ti3(Ge1-xSix)C2(x=0, 0.5, 1)固溶体体系进行系统的研究，对比分析其晶格结构、电子结构、力学和热学性能的变化趋势，以及Si掺杂对Ti3(Ge1-xSix)C2固溶体性质的影响.

2 理论模型与计算方法

本文采用基于密度泛函理论(DFT)的第一性原理计算方法(CASTEP软件包)，对Ti3(Ge1-xSix)C2(x=0, 0.5, 1)固溶体体系进行模拟计算. 计算中，电子之间的交换相关能用GGA-PBE泛函计算，离子实与价电子之间的相互作用用平面波超软赝势处理，其中Ti、Si、Ge和C的价态分别为3s23p63d24s2、3s23p2、4s24p2和2s22p2. 布里渊区积分k网格采用16164取样方法，平面波截断动能取500 eV，自洽迭代收敛精度设置为1×10-6eV/atom，应力的收敛标准设为0.01 eV/Å，最大应力偏差精度设置为0.05 GPa.

3 结果与讨论

3.1 Ti3(Ge1-xSix)C2体系的晶体结构和热力学稳定性

Ti3GeC2、Ti3(Ge0.5Si0.5)C2和Ti3SiC2都是三元层状化合物，属六方晶系(空间群为P63/mmc)，晶体结构如图1所示. 从图1可以看出，每个晶胞内有两个Ti3(Ge1-xSix)C2(x=0, 0.5, 1)分子，共包含12个原子. 其中3个Ti1原子占据2a(0, 0, 0)位置，3个Ti2原子占据4f(1/3，2/3，0.1290)位置，2个A位原子(Ge/Si)占据2b(0, 0, 1/4)位置，4个C原子占据4f(1/3,2/3,0.5701)位置.

图1 Ti3(Ge1-xSix)C2 (x=0, 0.5, 1)固溶体的晶体结构Fig.1 Crystal structure of Ti3(Ge1-xSix)C2 (x=0, 0.5, 1) solid solutions

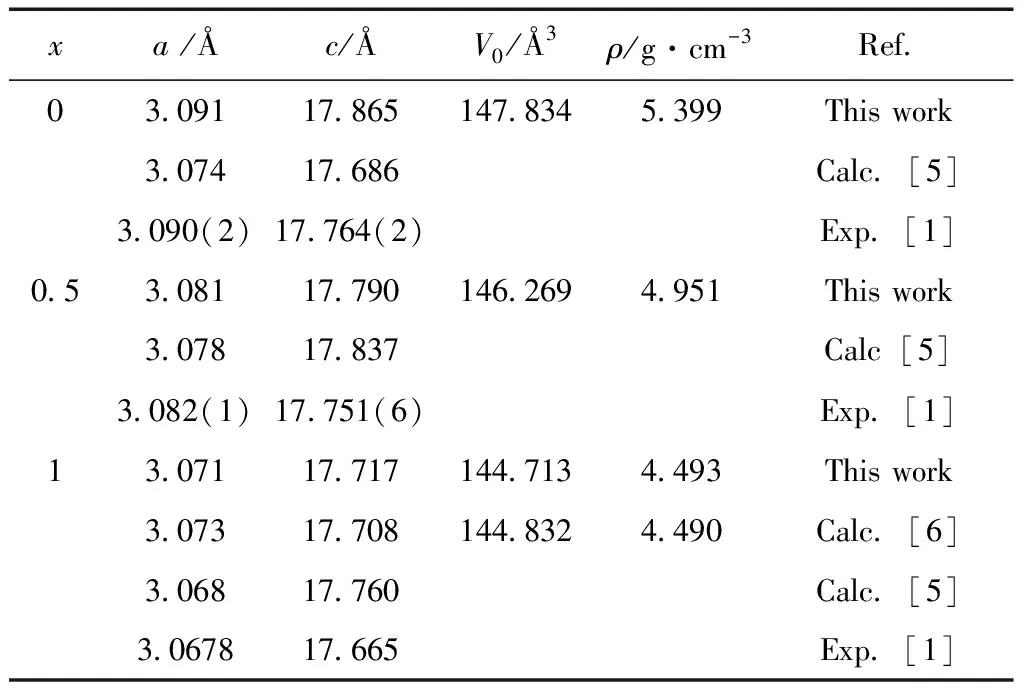
首先，对Ti3(Ge1-xSix)C2进行结构优化，表 1列出了优化后的晶体结构参数以及前人的理论和实验值. 从表1可以看出，本文的理论计算值与相关理论和实验结果均符合的很好. 此外，从图1可以看出，共边TiC6正八面体原子层与A原子层交替排列， C原子位于 Ti6C八面体的中心. 在TiC6正八面体中Ti-C键长为：Ti1-C:2.200 Å，Ti2-C:2.089 Å，键长较短，为强共价键，结合力更强，决定了它的熔点和弹性模量较高；A(A=Ge，Si)位原子层形成的平面将Ti3C2层隔开，两层A位原子间的相互作用力较弱，决定了它的自润滑性能较好，这些结构特点决定了Ti3(Ge1-xSix)C2(x=0, 0.5, 1)固溶体兼备陶瓷和金属的双重性能.

表1 计算所得Ti3(Ge1-xSix)C2(x=0,0.5,1)固溶体的晶格常数(a和c),原胞体积(V0)和密度 (ρ),以及其他理论或实验值

Table 1 Calculated lattice parameters (aandc), unit cell volumes (V0) and densities (ρ) for the Ti3(Ge1-xSix)C2(x=0,0.5,1) solid solutions together with other results.

xa /Åc/ÅV0/Å3ρ/g·cm-3Ref.03.09117.865147.8345.399This work3.07417.686Calc.[5]3.090(2)17.764(2)Exp.[1]0.53.08117.790146.2694.951This work3.07817.837Calc[5]3.082(1)17.751(6)Exp.[1]13.07117.717144.7134.493This work3.07317.708144.8324.490Calc.[6]3.06817.760Calc.[5]3.067817.665Exp.[1]

为了研究固溶体的热力学稳定性，我们计算了晶体的内聚能(Ecoh)和形成焓(ΔHm)，对于Ti3(Ge1-xSix)C2体系，计算公式如下：

(1)

(2)

其中，Etotal(Ti3(Ge1-xSix)C2)是Ti3(Ge1-xSix)C2化合物的晶胞优化之后的总能量；Eiso(Ti),Eiso(Ge),Eiso(Si)和Eiso(C)分别是Ti，Ge，Si, C单个原子在长为15 Å的立方晶胞内的能量；Ebulk(Ti),Ebulk(Ge),Ebulk(Si)和Ebulk(C)分别是Ti，Ge，Si, C的晶胞在最稳定状态下的单个原子能量；x是Si的取代浓度. 为了判断Ti3GeC2化合物中是否能稳定掺杂Si，我们还计算了Ti3(Ge1-xSix)C2化合物相关的竞争相化合物的形成焓，计算公式如下：

ΔHcp=Etotal(Ti3(Ge1-xSix)C2)-E(竞争相)

(3)

表2给出了计算所得Ti3(Ge1-xSix)C2(x=0, 0.5, 1)化合物的内聚能Ecoh，形成焓ΔHm和竞争相化合物的形成焓ΔHcp以及可能存在的竞争相化合物. 通过表2可以得知，Ti3(Ge1-xSix)C2化合物的内聚能和形成焓都小于零，说明Ti3(Ge1-xSix)C2化合物是热力学稳定的结构. 形成焓ΔHm小于竞争相化合物的形成焓ΔHcp，说明Ti3(Ge1-xSix)C2体系都是热力学稳定的. 根据计算公式(1)可知，内聚能的绝对值越大晶体键合力越强，从表2中看出Ti3GeC2、Ti3(Ge0.5Si0.5)C2到Ti3SiC2的内聚能逐渐减小，说明Si的浓度越高，Ti3(Ge1-xSix)C2化合物越稳定.

3.2 Ti3(Ge1-xSix)C2体系的弹性和力学性能

材料的弹性常数(Cij)决定晶体对于外界应力的响应，是反映材料弹性性能多种强度的重要物理量，根据材料的弹性常数可得出材料的力学稳定性、各向异性、刚度和脆性等相关力学性能.

表2 计算所得的Ti3(Ge1-xSix)C2(x=0, 0.5, 1)固溶体的内聚能(Ecoh, eV/atom),形成焓(ΔHm, eV/atom)以及竞争相的形成焓(ΔHcp, eV/atom)和可能存在的竞争相

Table 2 Calculated cohesive energies (Ecoh, eV/atom), formation enthalpies (ΔHm, eV/atom) and formation enthalpies relative competing phases (ΔHcp, eV/atom) and the most competing phases for the Ti3(Ge1-xSix)C2(x=0, 0.5, 1) solid solutions.

CompoundsEcohΔHmΔHcpMost competing phaseTi3GeC2-8.969-0.903-0.164Ti2GeC, TiCTi3(Ge0.5Si0.5)C2-9.025-0.890-0.148Ti2SiC, Ti2GeC, TiCTi3SiC2-9.083-0.877-0.138Ti2SiC, TiC

为了进一步研究Ti3(Ge1-xSix)C2的力学性能，在结构优化的基础上，计算给出了Ti3(Ge1-xSix)C2体系的弹性常数和弹性模量等. 由于Ti3(Ge1-xSix)C2化合物属六方晶系，因此它有5个独立的弹性常数(C11, C33, C44, C12和C13)，根据六方晶体玻恩力学稳定性判据[7]：

C11-C22>0，C44>0，

(4)

表3给出了计算所得Ti3(Ge1-xSix)C2化合物的弹性常数和其他理论值. 由表3可以看出Ti3(Ge1-xSix)C2化合物均满足玻恩力学稳定性判据，说明Ti3(Ge1-xSix)C2化合物都是力学稳定的. 此外，晶体材料的各向异同性在工程和晶体物理学中有着重要的应用，并且Ti3(Ge1-xSix)C2的各向异同性可以由弹性常数导出的三个参数来判断[8]：

(5)

其中，由Δp可以判断晶体压缩波(P)的各向异同性，由Δs1和Δs2可以判断晶体剪切波垂直于基面的波(S1)和基面上的偏振波(S2)的各向异同性，如果Δp、Δs1和Δs2的值等于1，则材料是各向同性的，如果Δp、Δs1和Δs2的值与1的差值越大意味着材料的弹性各项异性越强. 从表3的数据中看出三种参数的值都不为1，说明Ti3(Ge1-xSix)C2是弹性各向异性材料.

表3 计算所得的Ti3(Ge1-xSix)C2(x=0, 0.5, 1)固溶体的弹性常数 (in GPa)和各向异性参数Δp、Δs1和Δs2

Table 3 Calculated elastic constants (in GPa) and anisotropy parametersΔp,Δs1andΔs2for the Ti3(Ge1-xSix)C2(x=0, 0.5, 1) solid solutions.

xc11c12c13c33c44ΔpΔs1Δs2Ref.0334.894103.17391.752313.913140.4380.9370.8281.212This work373.1186.9991.80347.22144.97Calc.[5]0.5340.995101.02098.656328.846148.7060.9640.7941.239This work364.8782.2992.66343.69151.87Calc.[5]1355.51793.591103.521340.217166.1600.9570.7351.269This work372.6184.2095.39350.73155.37Calc.[5]365.886.999.8356.3163.9Calc.[6]

弹性模量是衡量材料抵抗弹性形变能力的参数，其值越大，使材料发生一定弹性形变所需的应力也越大，即材料刚度越大. 材料的弹性模量包括体积弹性模量(B)、剪切弹性模量(G)和杨氏模量(E)等. Ti3(Ge1-xSix)C2材料的体积弹性模量和剪切弹性模量可以利用公式(6)和公式(7)的Vogit-Reuss-Hill 模型[9-11]由弹性常数计算得出

BR=1/[(2S11+S33)+2(S12+S13)],

B=(BV+BR)/2,

(6)

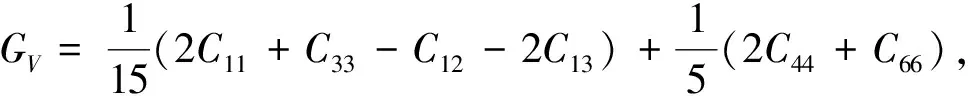
GR=15/[4(2S11+S33)-42(S12+2S13)+

3(2S44+S66)],G=(GV+GR)/2

(7)

计算结果见表4. 对表4中数据进行分析可知，Ti3(Ge1-xSix)C2化合物的弹性模量随着Si替代浓度的提高而增大，弹性模量数值的增加意味着材料刚度的增加，这与之前对其弹性常数的讨论结果一致. 此外，根据G/B的值能够判断材料是脆性还是延展性材料，其中G/B =0.57是区分脆性材料与延展性材料的临界值[12, 13].若G/B的值小于0.57, 该材料为延展性; 若G/B的值大于0.57, 则该材料为脆性. 由表4中可以看出Ti3(Ge1-xSix)C2化合物的G/B值均大于0.57，说明Ti3(Ge1-xSix)C2材料均为脆性材料. 同样能反映材料弹性性质的参数还有杨氏模量E和泊松比σ. 以上参数的计算结果见表4，计算结果表明Ti3(Ge1-xSix)C2材料的杨氏模量随Si含量的增加而增大，与体积弹性模量和剪切弹性模量变化情况类似. 泊松比可以用来衡量材料的韧脆性， 由于Ti3(Ge1-xSix)C2化合物的泊松比均小于1/3，说明材料是脆性的，与之前根据G/B值判断的结果一致.

3.3 Ti3(Ge1-xSix)C2固溶体电子结构和成键特性

为了研究Ti3(Ge1-xSix)C2固溶体化合物的成键特性，计算分析了该体系的电子结构:电子总态密度(Density of State，DOS)和分波态密度(Partial Density of State，PDOS)，见图2. 由图2可看出Ti3(Ge1-xSix)C2固溶体的电子态密度分布以及变化趋势较为相似，其价带和导带在费米面处有交叠，说明该体系材料均具有金属特性. 在费米能级以上，0—3 eV光子能量区间内Ti的3d电子贡献最大，Ge、Si、C的p电子也有少量贡献. 在费米能级以下，-6—-1 eV光子能量区间内贡献主要来自于C的2p电子和Ti的3d电子，其次是A原子(Ge、Si)的p电子的贡献. 因此在此区间内Ti-3d与C-2p杂化所成的Ti-C键占主导地位，其次为Ti-3d与Ge-4p、Si-3p杂化所成的Ti-A键，其中Ti-C的强相互作用对材料的稳定性起着重要作用. 在-12—-9 eV能量区间内C的2s电子做主要贡献. 在-6—-1 eV能量区间内C-2p电子和Ti-3d电子之间的杂化作用说明了Ti-C键的共价键性质，而Ti-A键、A-A键相对较弱. 通常键能越大键长越短，材料结构越稳定. 由于Ti3(Ge1-xSix)C2化合物的层状结构，根据以上分析可以得出Ti-A键为金属键，Ti-C键为共价键，这决定了Ti3(Ge1-xSix)C2化合物兼具陶瓷性与金属性的属性.

表4 计算所得的Ti3(Ge1-xSix)C2(x=0,0.5,1)固溶体的体积弹性模量 (in GPa) BV, BR和B=(BV+BR)/2, 剪切模量(in GPa) GV,GR和G=(GV+ GR)/2, G/B, 杨氏模量E以及泊松比的值

Table 4 Calculated bulk moduli (in GPa) BV,BRand B=(BV+BR)/2, shear moduli (in GPa) GV,GRand G=(GV+ GR)/2, G/B, Young's moduli E (in GPa) and Poisson's ratios σ for Ti3(Ge1-xSix)C2(x=0, 0.5, 1) compounds

图2 Ti3(Ge1-xSix)C2 (x=0, 0.5, 1)固溶体的态密度Fig. 2 Densities of state of the Ti3(Ge1-xSix)C2 (x=0, 0.5, 1) solid solutions

3.4 Ti3(Ge1-xSix)C2固溶体的热力学性能

(8)

其中,kB，NA和h分别为玻尔兹曼常数、阿伏伽德罗常数和普朗克常数;ρ，n和M分别为材料的密度、分子中原子的数目和分子质量；vm是平均声子波速, 可以由以下公式计算[15]：

(9)

表5给出了计算所得的Ti3(Ge1-xSix)C2固溶体体系的德拜温度(ΘD)以及声速(vl,vt和vm). 从表5可看出, Ti3(Ge1-xSix)C2材料具有较高的德拜温度，表明Ti3(Ge1-xSix)C2晶体中异种原子之间的共价性较强, 因此Ti3(Ge1-xSix)C2材料的结构较稳定, 这与之前根据形成焓数据和电子态密度(DOS)分析所得的结论一致.

MAX相陶瓷材料的晶格热导率(κph)源自于声子与声子的散射，晶格热传导可以看作声子扩散运动的结果.陶瓷材料的晶格热导率对于制作绝热与导热器件的应用有重要意义，Ti3(Ge1-xSix)C2晶体的晶格热导率κph可以用Slack基于Debye模型得出的经验公式[16]来计算：

(10)

式中M为平均原子质量(单位kg/mol)，ΘD为计算所得的德拜温度，δ3为原胞内每个原子的平均体积(单位m3)，γ为Grüneisen参数(单位(W·mol)/(kg·m2·K3)),其值可由泊松比(σ)得出，A是比例系数，大小取决于γ的值，n为晶胞中原子的数目, T为绝对温度. 其中，Grüneisen参数γ由以下公式给出[17]：

(11)

比例系数A可以由以下公式得到[18]：

(12)

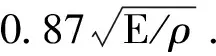
(13)

其中,kB，vm和Λmin分别是玻尔兹曼常数，平均声子波速和声子平均自由程，NA和ρ分别是阿伏伽德罗常数和晶体的密度.

此外，晶体的熔点(Tm)是在一定压强下材料从固相转变为液相的温度，一种物质熔点的高低取决于分子间作用力的大小，它反映的是材料是否耐高温的性质. 晶体的熔点可由弹性常数(Cij)通过下述经验公式计算得出[20]：

(14)

为了研究Ti3(Ge1-xSix)C2(x=0,0.5,1)固溶体的热力学性能，我们计算了Ti3(Ge1-xSix)C2固溶体在300K温度时晶格热导率、最小晶格热导率以及熔点. 计算结果见表5.

表5 计算所得的Ti3(Ge1-xSix)C2(x=0, 0.5, 1)固溶体的声子速度vl,vt和vm(m/s), 德拜温度ΘD(K),熔点Tm(K),在300 K温度下的晶格热导率κph(W/(mK)和最小热导率κmin(W/(mK))

Table 5 Calculated sound velocitiesvl,vtandvm(m/s), Debye temperaturesΘD(K), melting pointsTm(K), lattice thermal conductivitiesκph(W/(mK)) at 300 K, and minimum thermal conductivitiesκmin(W/(mK)) for Ti3(Ge1-xSix)C2(x=0,0.5,1) solid solutions.

XvlvtvmΘDTmκphκminRef.07932.54815.66139.8628.31829.627.5221.0013This work0.58434.35128.16535.1671.11870.330.5861.0734This work19100.85609.97118.3733.61930.938.9381.1776This work

从表5可以看出，Ti3(Ge1-xSix)C2固溶体有较高的熔点Tm，熔点随着Si含量的增加从1829.6 K增加到1930.9 K，这表明Ti3(Ge1-xSix)C2固溶体具有稳定的晶格结构，并且其稳定性随着Si含量的增加而增强，可以将其用于制作耐热材料. 同时Ti3(Ge1-xSix)C2固溶体在300 K温度时的晶格热导率κph稍低于金属，与多数合金的热导率相近，其值同样随着Si含量的增加而增加，这说明在室温下Ti3(Ge1-xSix)C2材料有着较好的导热性，并且其导热性能随着Si含量的增加而增强，因此Ti3(Ge1-xSix)C2固溶体材料有望用于一些电子元器件的封装材料.

4 结 论

综上所述，本文采用基于密度泛函理论的第一性原理计算方法，系统研究了Ti3(Ge1-xSix)C2(x=0, 0.5, 1)固溶体的晶格结构、热力学稳定性、电子结构以及热力学性能，并分析以上性质随Si取代浓度变化而发生的改变.研究结果表明，这些化合物均为力学和热力学稳定结构，并且为脆性材料，同时还显示出了金属特性；从电子结构层面分析，Ti-Ge/Si键为金属键，Ti-C键为共价键.Ti3(Ge1-xSix)C2固溶体的力学性能随Si取代浓度的增加而提高，因此在实际应用中可以通过适当的Si掺杂来得到较好力学性能的材料.Ti3(Ge1-xSix)C2固溶体由于具有相对较高的德拜温度和高熔点以及在300 K温度下有着较高的晶格热导率，表明所有的Ti3(Ge1-xSix)C2固溶体具有稳定的晶格结构以及良好的导热性能，因此Ti3(Ge1-xSix)C2固溶体材料有望用于电子元器件的封装材料.