初中数学命题方法之延续策略

姜晓翔

（浙江省湖州市南浔区教育教学研究和培训中心）

对于数学教师而言，命题能力是其专业发展中需要具备的重要基本数学素养之一，既能反映教师对于学生学习情况了解的精准度，又决定着课堂教学的效率与思维的深度.因此，笔者认为，无论是教研人员还是一线教师，都需要重视对于命题这一能力的培养，即命题研究.

有一种情怀叫传承，有一种命题方式叫延续，即以延续历年中考试题的优秀特征而重新命制新题的方法与策略.近年来，笔者负责或参与了多次区、县级中考数学模拟试题的命制，以及中考试题的命制，略有所感，与同仁分享、共勉.下面主要从优质素材、位置结构、解题方法、问题探究几个方面来说明延续策略的具体操作方式与实效.

一、对于优质素材的延续，追求创新特色

近年来，各地区的中考试题不断创新，PISA、核心素养、STEAM等前沿理念不断地被融入进中考试题中，让原本枯燥乏味的数学试题变得充满生机与活力.对于命题者而言，题目的质量高低某种程度上取决于对有价值素材的选取，故寻找好素材是命题者孜孜不倦的追求.

案例1：对一道七巧板试题的改编.

原题1（2017年浙江·湖州卷）七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图1所示的七巧板拼成的，则不是小明拼成的那幅图是（ ）.

图1

针对此题，笔者进行如下改编.

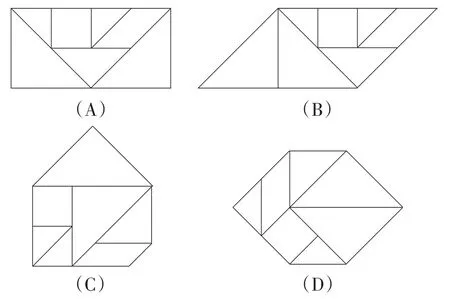
七巧板是我国祖先的一项卓越创造.爱思考的小红同学用如图2所示的七巧板拼成了如图3所示的四幅图，则这四个图形的周长从大到小排列正确的是（ ）.

图2

图3

（A）乙＞丙＞甲＞丁 （B）乙＞甲＞丙＞丁

（C）丙＞乙＞甲＞丁 （D）丙＞乙＞丁＞甲

原题1的特色明显，形式创新.命题者通过观察生活中的益智类玩具——七巧板，发现每块特殊多边形的边长存在着一种特定的数量关系，从而巧妙地编制出这样一道基于核心素养的PISA试题.基于原题1的改编题，不仅可以让学生感受到七巧板的强大魅力，还可以通过数学思考去探索其中蕴含的数学魅力.尽管改编题计算量稍大，但还是能充分体现对学生数学素养的考查功能.据笔者了解，其他地区的中考模拟试卷和2018年中考试卷中也有出现以七巧板为素材的试题，这无疑遵循了对优质素材的延续这一命题策略.

二、对于位置结构的延续，追求触类旁通

在探究类中考热点试题中，不乏一些对特殊位置状态下图形的研究，如通过平移、旋转及折叠等变换之后形成的特殊位置.而在这些特殊位置下，往往存在着某些边、角的特殊数量关系或位置关系，对于这些关系的探究也是当今中考的热点问题.笔者热衷于对这些热点问题进行研究，力求将其特殊的位置结构得以延续，从而命制出新的题目，并加以触类旁通，充分发挥其潜在的探究价值与评价功能.

案例2：对一道几何探究型试题的改编.

原题2（2016年江苏·泰州卷）已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA，EC．

（1）如图4（1），若点P在线段AB的延长线上，求证：EA=EC；

（2）若点P在线段AB上．

①如图4（2），连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由；

②如图4（3），设AB=a，BP=b，当EP平分∠AEC时，求a∶b的值及∠AEC的度数．

图4

针对此题，笔者进行如下改编.

已知菱形ABCD，∠ABC=α，P为射线AB上的一点，以BP为边作菱形BPEF，使点F在线段CB的延长线上，连接EA，EC.

（1）如图5（1），若点P在线段AB的延长线上，求证：EA=EC；

（2）若点P在线段AB上，且α=120°.

①如图5（2），连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由；

②如图5（3），设AB=2a，BP=2b，当EP平分∠AEC时，求的值.

图5

上述改编题的命制过程是对原试题中图形位置结构的一种传承，延续了原题2中两个特殊四边形的三种特殊的位置结构特征，只是将原题2的两个正方形改为两个含60°内角的菱形.如此改编，对于前两问，形变质不变.第（1）小题依然是通过三角形全等证得结论成立，只不过在证明夹角相等时需要通过公共角进行转化；对于第（2）小题第①问，原题2是通过两个45°角的和证明垂直，改编题是通过一个30°角与一个60°角的和证明垂直.然而，第（2）小题第②问通过改编略微提升了难度.原题2只需要利用一对相似三角形中的成比例线段即可求出的值，但改编题需要添加辅助线构造出相似三角形才能解决问题，从思维的考查立意要求来看，明显有所提高.

改编题的命制还得到了意外之喜，因为解决此题第（2）小题第②问的思路方法较多，起到了很好的拓宽思维的效果，现列举几种典型的解题思路.

思路1：如图6，连接PF，交EC于点M，通过证明△EMP∽△CMF，可求得.

图6

图7

思路2：如图7，过点A作AH⊥FB于点H，分别交EP，EC于点G，M，通过证明△EGM∽△CHM可求得结果.

Thus,hyperglycemia induces oxidative stress,which contributes to the accumulation of toxic products,which in turn leads to atherogenic modification of m-LDL,endothelial dysfunction and atherosclerosis progression in patients with diabetes.

思路3：如图8，延长CF至点M，使FM=EF，连接EM，通过证明△AEP∽△ECM可求得结果.

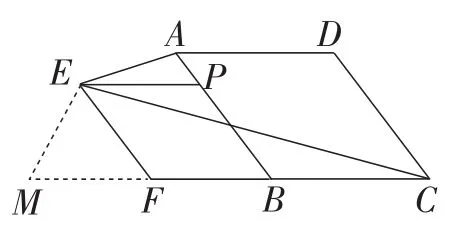
图8

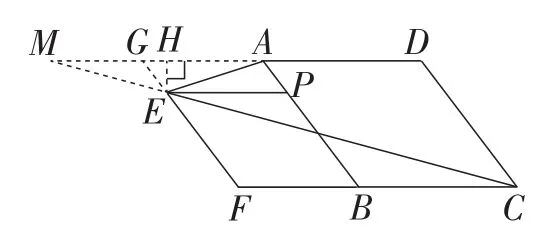
图9

思路4：如图9，延长CE，与DA的延长线交于点M，延长FE，与AM交于点G，过点E作EH⊥AM于点H，通过证明△MGE∽△CFE可求得结果.

其实解决此题的思路远不止于此.对中考试题进行改编不仅能起到触类旁通的效果，还能通过一题多解拓宽学生的思维.

三、对于解题方法的延续，追求通性、通法

解题教学的目的是为了让学生更好地掌握解决问题的通性、通法.高质量的中考试题中往往渗透着重要的解题的通性、通法，如果能将重要的解题方法延续到一道全新的题目中，这将会是一种很好的命题策略.笔者带着这样的命题思考，不断地尝试着对中考试题进行改编，效果颇佳.这不仅延续了中考试题中所渗透的解题通法，而且能使学生进一步巩固与完善该解题通法在不同形态下的体现与优化.

案例3：对一道动点最值类试题的改编.

原题3（2017年贵州·贵阳卷）如图10，在矩形纸片ABCD中，AB=2，AD=3，E是AB的中点，F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是_____．

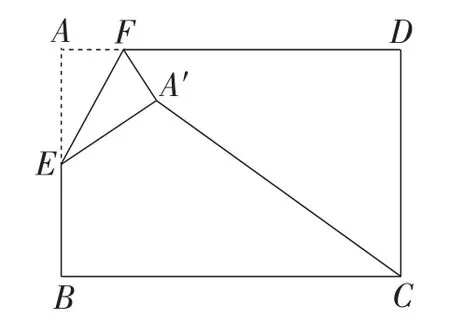
图10

针对此题，笔者进行如下改编.

如图11，在△ABC中，∠A=120°，AB=4，AC=5，D是AC上一点，且DC=3，E是BC边上的一个动点，连接DE，将△CDE沿DE所在直线翻折，得到△FDE，则点B与点F之间的距离最小值是______.

图11

原题3是一道求定点到动点距离的最值问题，此类问题首先要分析出动点运动的轨迹是什么.由翻折的性质不难发现EA′的长始终为2，于是动点A′的运动轨迹为圆.如图12，当C，A′，E三点共线时，A′C的最小值为.此题的解题方法在近年来的最值问题中实属常见.于是，笔者通过解题方法的延续策略命制了一道新的题目.

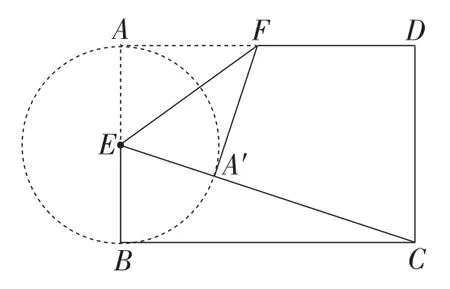
图12

改编题的初稿只是将原题中的矩形变式为直角三角形，如图13所示.然而，笔者认为，如此命制虽然起到了延续解题方法的作用，但与原题相仿程度过高，不甚理想.因此，就有了∠BAC=120°的改编，着实增加了BD的计算难度，如图14所示.改编题不仅延续了原题的解题方法，还增加了学生的思维厚度，从而赋予了其更好的评价功能.

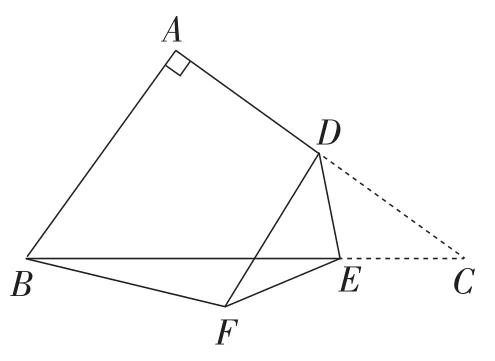
图13

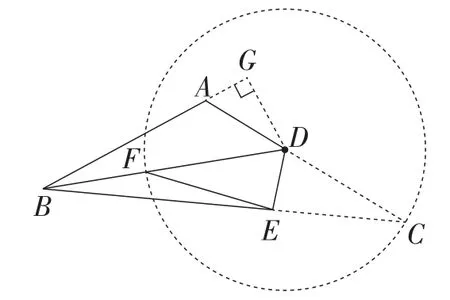
图14

四、对于问题探究的延续，追求思维生长

近年来，中考数学试题的命制从原来的“以知识立意”向“以能力立意”转化，强调由“知识测量型”向“能力测量型”转变，更加注重考查学生继续学习的潜能，注重考查学生的数学核心素养和创新能力.新定义型探究类问题是近年来中考数学命题创新的一个显著特点，它因具有新颖性、开放性、创造性和综合性的特点而深受命题者青睐.然而，当命题者对于命制出一个全新的新定义型试题存在困难时，可以对已有的高质量中考试题进行改编.可以尝试着将原中考试题的探究方向继续深入下去，让探究得到进一步延续，这何尝不是一种好的命题方式呢.

案例4：对一道新定义型试题的改编.

原题4（2016年浙江·衢州卷）如图15，我们把对角线互相垂直的四边形叫做垂美四边形．

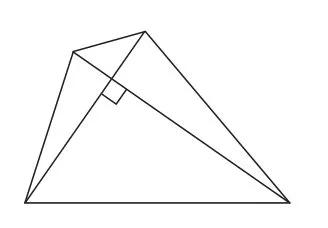
图15

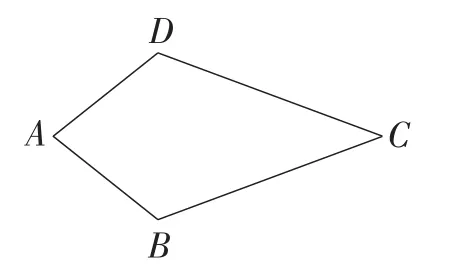
图16

（1）概念理解：如图16，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？并说明理由．

（2）性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．

猜想结论：_______（要求用文字语言叙述）．

写出证明过程（先画出图形，写出已知、求证）．

（3）问题解决：如图17，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5，求GE长．

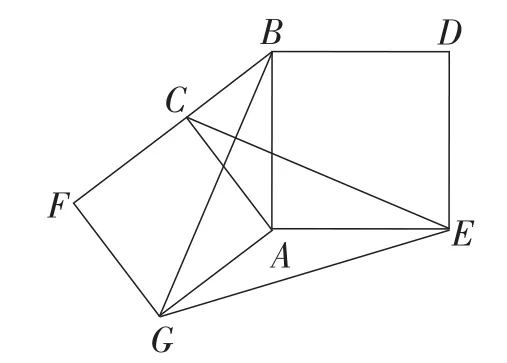
图17

针对此题，笔者进行如下改编.

（1）概念理解：如图18，已知在菱形ABCD中，对角线AC与BD交于点O，，问菱形ABCD是垂比四边形吗？试说明理由．

图18

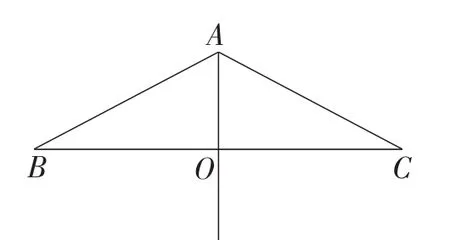
图19

（2）尝试探究：如图19，已知在等腰三角形ABC中，AB=AC=2，O是边BC的中点，tan∠BAO=2，问在射线AO上是否存在点D，使得四边形ABDC是垂比系数为2的垂比四边形.若存在，试求出此时线段OD的长；若不存在，试说明理由．

（3）问题解决：如图20，分别以Rt△ABC的斜边AC和直角边AB为边向外作Rt△ACD和Rt△ABE，且∠CAD=∠BAE=90°，连接DE，已知AE=1，BC=2，当四边形BCDE是垂比系数为3的垂比四边形时，求DE的长．

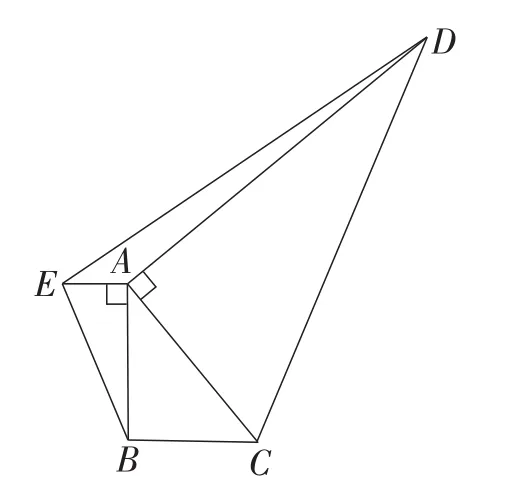
图20

上述改编题中的第（1）（2）小题较为容易，而第（3）小题的思维层次有了较大的飞跃.第（3）小题中，如图21和图22，连接BD，EC，通过证明△EAC∽△BAD，得到AB=3AE=3或两种情况.

图21

图22

原题4是一道经典的新定义型探究问题，以垂美四边形的“新定义理解—性质探究—解决问题”为探究主线，设置了层层递进的三道小题，充分发挥了其过程学习型的评价功能.笔者以此题中的核心条件“对角线互相垂直”为突破口，发现垂直是位置关系，假如再增加一个数量关系，是否能赋予试题新的探究价值与评价功能呢？于是，笔者就对互相垂直的两条对角线增加了一个“比值为某一具体整数”的条件，将垂美四边形变式为垂比四边形，命制出上述改编题.从垂美四边形到垂比四边形，虽然只一字之差，但是从题目的难度，以及思维的深度来看，融入了对相似三角形的对应边成比例的考查，渗透了分类讨论的数学思想，既明显提升了对学生的思维层次的要求，又在延续原题探究问题的基础上达到了思维的生长.

五、结束语

初中数学题的命制是一门高深的教学艺术.不会命题的教师很难成为真正的优秀教师.可见，命题的技术对于一线教师来说，体现了把握教学标准的能力.本文只是笔者对于近几年命题实践的不太成熟的点滴体会，由于水平和经验有限，必定存在着诸多瑕疵，望读者能批评指正.同时，文中所阐述的命题方法之延续策略还不够完善，必然还存在对于其他优秀特征的延续，待今后在命题实践中不断地探索与完善.