从一节“看上去很精彩”的新授课说起

雍思贤

（重庆市綦江区三江中学）

在2018年送教下乡期间，笔者曾听了一节人教版《义务教育教科书·数学》八年级上册（以下统称“教材”）“13.3等腰三角形”（第1课时）的新授课.本节课的教学设计完整、内容丰富、教学流畅.现呈现本节课的部分教学环节，并提出笔者的思考与建议.

一、重回课堂，再现“精彩”环节

1.复习引入

为了创设一个引人入胜的问题情境，执教教师精心制作了微课.其微课声音悦耳，画面美观，脚本描述如下.

我国著名的数学家华罗庚曾经说过，宇宙之大，地球之变，日用之繁，无一处不用数学.从古埃及气势磅礴的金字塔到我们中国雄伟壮丽的深圳之窗，随处皆可见数学的影子.生活中，建筑工人在盖房子时，用一块等腰三角板放在梁上，在顶角的顶点系一个重物，如果系重物的绳子恰好经过三角板底边的中点，就表明房梁是水平的，你知道其中的道理吗？首先来复习一下，什么是等腰三角形呢？两边相等的三角形是等腰三角形.相等的两边是腰，另一边是底边，两腰的夹角是顶角，腰和底边的夹角是底角.怎样快速地找出等腰三角形的两个底角呢？其实，只要找出两腰的对角即可.请看，在△ABC中，腰AB的对角是∠C，腰AC的对角是∠B，所以，等腰三角形ABC的两个底角是∠C和∠B.

上述微课中提及了数学家的经典话语，呈现了生活中的等腰三角形模型，创设了生活中的问题情境，回顾了等腰三角形的相关概念，激发了学生的学习兴趣和探究欲望，看上去是一个很精彩的情境引入.

2.探究新知

在探究等腰三角形的两条性质时，教师按以下几个步骤实施教学：让学生用折纸法剪出一个等腰三角形，并猜想它的两个底角具有怎样的关系；接着鼓励学生大胆验证，在学生采用度量法和折叠法验证之后，师生共同展开几何论证，画出如图1所示的等腰三角形ABC，并写出已知和求证．

图1

为了顺利证明等腰三角形ABC中∠B=∠C这个结论，教师引导学生观察之前剪出的等腰三角形模型中的折痕，从而找寻辅助线的作法，可以作△ABC的顶角平分线AD，作△ABC的底边中线AE，作△ABC中BC边上的高AH.

在探究出“等边对等角”这一性质之后，教师顺势追问“刚才我们画出了等腰三角形ABC的顶角平分线AD，底边上的中线AE和底边上的高AH，这三条辅助线是同一条线段吗？为什么？”

以下教学过程略.

就这样，教师引导学生亲身经历了“观察—猜想—验证”的过程，特别是“三线”（顶角平分线、底边上的中线和底边上的高）的构造，既顺利实现了对性质1“等边对等角”的逻辑验证，又轻松开启了对性质2“三线合一”的探究，如此一箭双雕，看上去很精彩．

二、“看上去很精彩”的课是不是真的精彩

本节课中，执教教师对课前的巧妙预设和课中的启发诱导，使教学过程得以顺利推进.乍一看，本节课的确精彩；但稍做思考，还有值得质疑和商榷之处.

1.采用微课来复习旧知合适吗？

如今，微课凭借内容短小精悍的优势进入课堂，成了课堂教学的一种有效补充.本节课中，执教教师通过自制的微课来“创设情境，引入课题”的做法值得充分肯定.然而，采用微课来复习旧知合适吗？建构主义认为，教师应当把学生原有的知识经验作为新知识的生长点，引导学生从原有的知识经验中生长出新的知识经验.《义务教育数学课程标准（2011年版）》（以下简称《标准》）指出，教学活动是师生积极参与、交往互动、共同发展的过程.而微课往往会让教师快速地讲、学生被动地听，省略了师生互动的环节，使学生缺乏充分思考的时间.因此，以微课的形式来复习旧知一定要慎重.

2.新授课仅仅是为了教学新知吗？

本节课中，经过学生的剪和折，再辅以教师的点拨，等腰三角形的两条性质得以顺利推出.课堂上，教师教得轻松，学生学得愉快.然而，轻松愉快的课堂就是精彩的课堂吗？答案当然是否定的.《标准》指出，数学教学不仅要使学生获得“四基”，还要求学生发展“四能”，培养其科学态度.课堂上，教师仅仅局限于“三线”的构造，只字未提其他的思路，没有引导学生反思构造辅助线的意图，没有引导学生总结“证明等腰三角形两个底角相等”的方法，阻碍了学生数学思维的发展.学生在教师的牢牢掌控和循循善诱之下顺畅地回答着、实践着，影响了反思、质疑等习惯的培养.建构主义认为，教学不是知识的传递，而是知识的处理和转换.教师不单是知识的呈现者，更应该重视学生对各种现象的理解.因此，新授课不能局限于对新知结论的教学，应该遵循建构主义原理.例如，让学生充分经历“动手操作—观察猜想—推理验证—得出结论”等过程，主动参与新知的形成过程，从而促进其思维的发展和能力的提升.

三、思考与建议

教师应该如何施教才能避免以上两点遗憾呢？笔者有以下几点建议.

1.削减微课篇幅，巧设复习环节

由于微课能先声夺人，造成学生渴望追求新知识的心理状态，所以本节课仍可以采用微课来创设情境.但学生在小学接触过等腰三角形，对等腰三角形的相关概念并不陌生，因此，教师可以对“复习引入”环节的微课进行“瘦身”，砍掉其中的复习环节，并将它融入到新知探究中.当学生动手剪出等腰三角形后，教师引导学生“找一找”“说一说”，以此来回顾等腰三角形的腰、底边、顶角和底角等相关概念.如此教学，汲取了微课引人入胜的精华，舍弃了微课单向传输的糟粕，诱发了学生主动复习旧知和建构新知的强烈欲望，使课堂教学得以有效推进.

2.夯实新知探究，启迪学生思维

尽管教师竭力引导学生添加了三种不同的辅助线，但学生不清楚为什么要添加这些辅助线.这种一带而过的教学有“形”无“魂”，不利于对学生思维的培养.数学家哈尔莫斯说过，问题是数学的心脏.因此，在学生思维的最近发展区设置一连串的关键问题，可以打破学生思维的平衡，引起学生的适度焦虑，从而通过学习去努力解决问题.为了证明“等腰三角形两个底角相等”这个猜想的正确性，学生写出已知、求证之后，教师的问题串就可以闪亮登场.在“剪一剪”和“折一折”的基础上，教师启发学生先画出一条辅助线（构造“三线”）证明两个三角形全等，接着尝试引出两条辅助线（两腰上的高）证明两个三角形全等，然后思考不添加辅助线也能证明一个三角形和自身全等，最后反思和总结证明两个角相等的常见方法.教师可以将问题串设计如下.

问题：根据最近所学的全等三角形知识，如何证明等腰三角形的两个底角相等呢？为什么可以这样证明？

预设：证明这两个角所涉及的两个三角形全等.因为全等三角形的对应角相等.

追问1：如何构造两个全等三角形呢？

预设：通过“三线”中的一种即可.

追问2：你还有哪些方法构造全等三角形？

追问3：刚才通过添加“等腰三角形底边上的高”这条辅助线，构造了两个全等三角形，你还有其他的添加方法吗？

师生活动：学生先独立思考，然后交流展示.如果学生遇到困难，教师引导学生画出两腰上的高.如图2，先作出等腰三角形ABC腰上的高BD和CE，并用面积法得出两腰上的高相等，再证明△BCE≌△CBD，得出∠ABC=∠ACB.

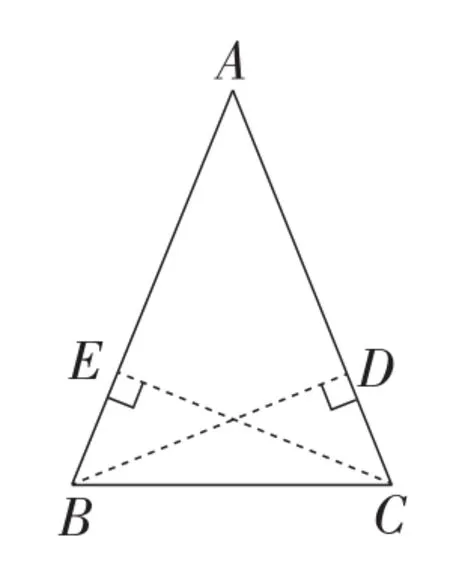
图2

追问4：刚才我们添加的这些辅助线，有什么共同的目的呢？

预设：构造全等三角形.

师生活动：通过师生互动得出“等边对等角”的结论，并启发学生将它翻译成符号语言.

追问5：对于含钝角的等腰三角形，以上方法还适用吗？请大家课后去完成.

预设：既可以构造“三线”，也可以画出如图3所示的图形.对照图2，用类比的方法即可以证明.

图3

追问6：在等腰三角形中，如果不画辅助线，可以证明∠B和∠C这两个底角相等吗？请大家课后去思考.

预设：用“SSS”证明△ABC≌△ACB.

追问7：现在有哪些方法可以证明两个角相等？你认为哪种方法更优越？

就这样，通过一连串的提问和追问，给学生营造一个学习不止、思维不断的探究氛围，使学生的思维水平不断提升.

3.开展数学活动，提高数学素养

积累活动经验是数学教学的重要目标，应贯穿在整个课程之中.数学活动隶属于“综合与实践”课程内容，是实现这个目标的有效载体.在本节课中，学生已经尝到了用三角形全等和面积法来证明两条垂线段相等的“甜头”，教师不能让学生的思维浅尝辄止，可以将教材第83页习题13.3第13题（等腰三角形两底角的平分线相等吗？两腰上的中线呢？两腰上的高呢？）和教材第89页活动3“等腰三角形中相等的线段”结合起来，专设课时组织学生开展自主学习、实践操作、归纳概括、质疑验证、总结反思等系列活动.通过数学活动的有效开展，可以帮助学生进一步巩固全等三角形和等腰三角形的重要性质，逐渐加深对轴对称性质的理解，及时总结证明两条线段相等和两个角相等的常见方法，从而积累数学活动经验，提高学生的数学素养.

四、再思考：新授课因何而“精彩”

为什么一节“看上去很精彩”的新授课却存在这么多问题？这引发我们再思考：什么样的课堂才称得上精彩？新授课因何而精彩？课堂是否精彩有诸多评价指标，但笔者认为，精彩的课堂必须以培养学生的核心素养为终极目标，教师至少要做到以下两点.

1.以学定教

课堂上教什么？教师除了帮学生达到《标准》的要求，还需要以学定教.

（1）立足课时目标.

教师在备课时要有起点意识，应根据学生的学情来确定每节课的教学目标和教学内容，并给学生留足思考的时间，使教学更深入、更彻底.本节课中，如果学生的学习基础较为薄弱，则可将新知应用移到下一节课去学习，只需探究出等腰三角形的两条性质即可，从而避免“蜻蜓点水，止于表面”的教学.

（2）胸怀长远目标.

课堂上重点教什么？那就是发展学生的数学核心素养，即培养学生的必备品格和关键能力.由于本节课隶属于“图形与几何”课程内容，因此，学生思维的训练和推理能力的发展应该贯穿在整个学习过程中.本节课中，执教教师应该从学生的认知规律出发，不仅要通过“剪一剪”“折一折”等几何实验来培养学生的直觉思维和创造性思维，还要利用三角形全等来证明等腰三角形的两条性质，让学生经历观察、实验、归纳、论证的认识图形的全过程，帮助学生完成由实验几何到论证几何的过渡，逐步培养和训练学生的逻辑推理能力.

2.以生为本

课堂上如何教？教育的出发点是什么？那就是“以生为本”.

（1）实施因材施教.

每个班级的学生都存在着一定的差异，教师应尊重学生的差异实施因材施教、分层教学.例如，在前文建议2的几个追问中，追问5和追问6只适合学有余力的学生；对于学困生，追问2和追问3也可以让他们自主选择，真正实现让不同的人在数学上得到不同的发展.

（2）落实师“导”生“演”.

有效的教学活动是教师教与学生学的统一.学生是学习的主体，教师是学习的组织者、引导者和合作者.课堂上，不但需要教师精心的“导”，通过有效的教学过程激发学生的学习兴趣，帮助学生获得有效的学习方法，形成良好的学习习惯，而且需要学生积极的“演”，通过实验观察、独立思考、合作交流、猜想验证、反思质疑等方式，切实提高学生的核心素养.

总之，评价一节课是不是精彩，不能只停留于课堂表面，不能只看教学流程是否流畅，不能只看学生是否学得轻松，等等.数学教学中，教师应该以数学核心素养为导向，着眼于学生的终身发展，重点关注新知的形成过程，重点训练学生的思维并培养学生的关键能力.