考虑尺度效应的微振动能量采集器建模

李创业， 霍 睿， 王伟科， 赵 辰

(1. 山东大学 机械工程学院，济南 250061； 2. 山东大学 高效洁静机械制造教育部重点实验室, 山东 济南 250061；3. 中国人民解放军32145部队 机要科, 河南 新乡 453000)

“物联网”[2-4]囊括了数以万计的传感器，传统供电方式因寿命短、储能有限、更换费用昂贵、污染环境等缺点[5]无法满足物联网持久、可集成、工作环境多变、环境友好型的供能需求，新型1供电技术的研究意义重大。压电式能量采集器[6]可以将机械能吸收转化为电能，具备能量转化效率高、结构简单紧凑、寿命长、环境友好、与微纳制造技术兼容等优势[7]。由于尺度效应，微结构力学性能与宏观模型分析结果不吻合[8-10]。而微压电悬臂梁是微振动能量采集器的一种基本结构形式。

基于此，本文首先验证了考虑尺度效应的悬臂梁模型，进而建立微振动能量采集器的改进模型。通过仿真和实验证明本文建立的采集器改进模型有效的降低了误差。改进模型为微供能设备的设计提供了参考依据。

1 微压电悬臂梁模型改进及验证

1.1 微压电悬臂梁动力学模型

不考虑尺度效应，微梁动力学模型是

(1)

文献[11]中引入表征尺寸效应的本征长度l，采用偶应力理论改进了微梁的动力学模型，得到运动控制方程如下

(2)

式中：h为微梁厚度，无量纲厚度h/l=3.5。根据振型叠加法，可以得到谐振频率

(3)

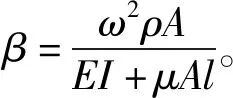
1.2 微压电悬臂梁有限元分析

由式(2)可知：在尺度效应影响下，μAl2是微悬臂梁刚度增大[12-15]的主要原因，为便于进行有限元分析，引入等效杨氏模量E1

(4)

微悬臂梁可简化为Si梁和PZT-5H两层结构。简化后Si的尺寸LSi×WSi×TSi：3 150 μm×1 000 μm×13 μm；PZT-5H的尺寸LPZT-5H×WPZT-5H×TPZT-5H：3 150 μm×1 000 μm×1.6 μm。引用文献[16]中的参数，结合式(4)可得等效杨氏模量，如表1所示。

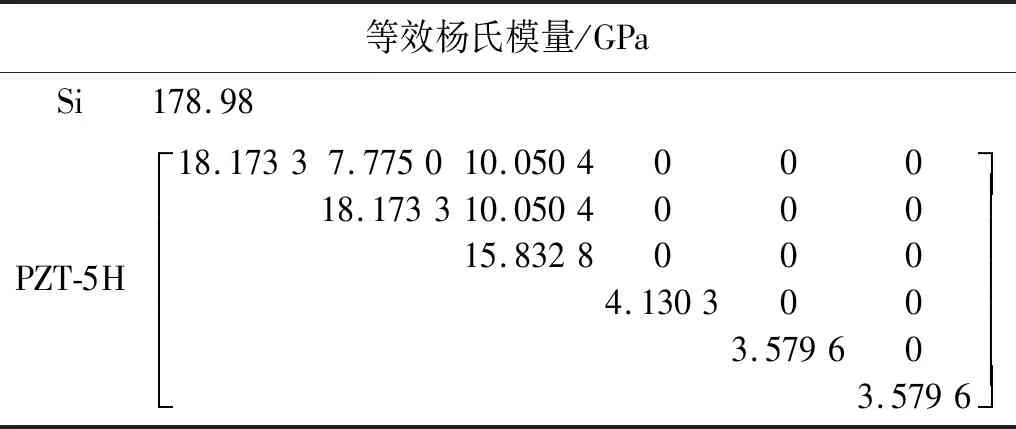
表1 材料的等效杨氏模量

对悬臂梁进行有限元分析，得到悬臂梁宏观与改进模型的一阶振型图，模态频率分别为1 536 Hz与1 803 Hz。如图1和图2所示。

图1 悬臂梁宏观理论模型有限元分析结果

图2 悬臂梁改进理论模型有限元分析结果

1.3 微压电悬臂梁制作与性能测试

在4 10.16 cm的SOI基片上采用光刻、溅射、溶胶凝胶、干法刻蚀等工艺完成制备与封装，其SEM图，如图3和4所示。

图3 微压电悬臂梁俯视图

图4 微压电悬臂梁厚度放大图

采用信号发生器(YE1311)、功率放大器(E5871A)、振动台(E-JZK-5)、激光测振仪(OFV505/5000)、数据采集卡(INTEST Main Unit INJ9008U-I)、加速度传感器(CA-YD-1182)等仪器搭建了如图5所示的悬臂梁振动特性实验平台。

图5 实验平台

当加速度激励为6 g(1 g=9.8 m/s2)时，在1 600～2 000 Hz范围内依次改变振动加速度的频率，并记录尖端位移的数据。采用功率谱对尖端位移进行处理，可得到功率谱值与振动频率的曲线，如图6所示。在1 818 Hz时，功率谱值达到最大，即为谐振频率。

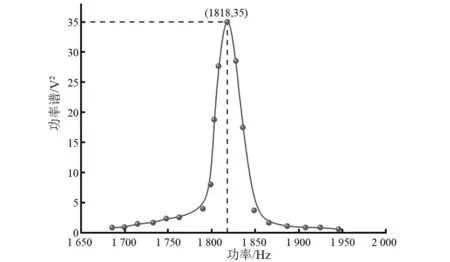
图6 尖端位移曲线的功率谱-频率曲线

由表2可知，宏观理论模型与实验测试的谐振频率相差282 Hz，误差是15.5%；而考虑尺度效应后，改进理论模型与实测结果相差15 Hz，误差是0.8%；

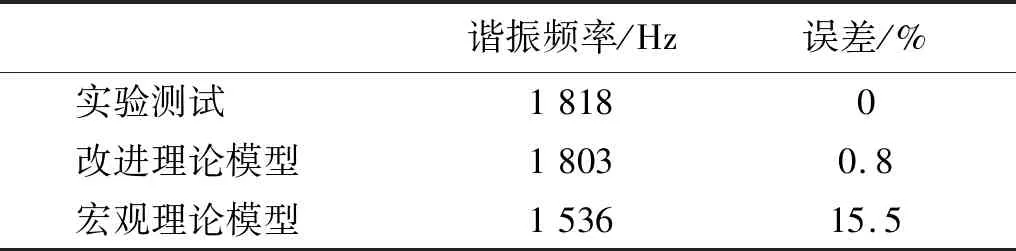
表2 实验测试频率和理论分析频率对比

2 微压电振动能量采集器建模及验证

由上一小节知，微梁的谐振频率在1 000 Hz以上，然而传感器周围环境中的低频振动较多。大量学者[17-19]通过在悬臂梁自由端附加Si或Ni质量块来减小谐振频率，使其能在低频振动环境中发挥作用。本文把Si质量块刻蚀到T型悬臂梁上，得到了“T型”采集器，采集器可简化为由PZT-5H、Si梁和质量块三层结构组成[20]。结构如图7所示。

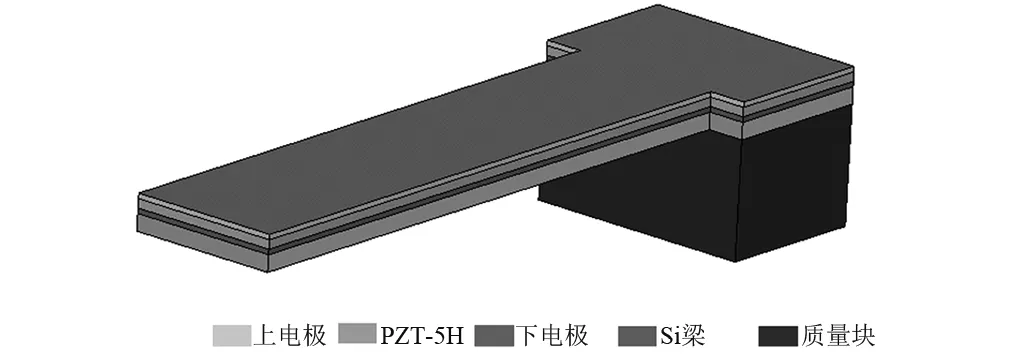
图7 T型采集器结构示意图

2.1 微振动能量采集器动力学模型

考虑尺度效应，并结合微梁的改进理论模型，采集器自由振动的动力学模型为

(5)

当除去式(5)中的μAl2时，模型自动退化为宏观理论模型。在给定的边界条件下，设谐振频率为ωr，振型函数为Wr(x)，第r阶模态质量Mr。引进正则坐标qr(t)，根据振型叠加原理，对微分方程解耦，可得

(6)

采集器形变产生的电荷Q集聚在PZT-5H的上下表面，形成电容器，容易得出

(7)

式中：Ss为极板正对的面积；εr为相对介电常数；Cs为等效电容。Vs是PZT-5H上、下表面之间的电势差，也是微振动能量采集器的开路输出电压。

2.2 微振动能量采集器有限元分析

有限元分析结果以云图的形式可以体现出采集器的实际运动状态。沿用表1中的等效弹性模量及文献[16]中相关参数，建立采集器有限元模型。设置固定端的自由度为零，加载幅值为1 g加速度激励后，输出电压和尖端位移在谐振频率300 Hz处均到达最大，输出电压为0.17 V，尖端位移为10.7 μm。

2.3 微振动能量采集器性能测试

设定加速度激励幅值为1 g，采用确定频率激励方式在50～500 Hz范围内对振动台进行激振，并在PC端观测记录加速度、自由端的尖端位移与输出电压。

图8、图9给出了采集器分别由宏观模型、改进模型以及实验测试所得的尖端位移-频率曲线、输出电压-频率曲线。各谐振点上的主要信息以及与实验结果的对比误差详见表3。

图8 微振动能量采集器的位移-频率曲线

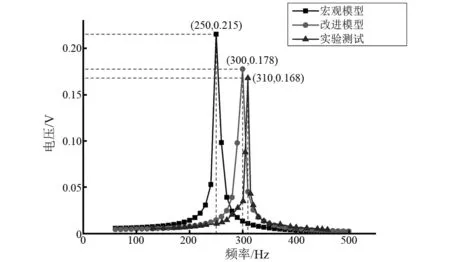
图9 微振动能量采集器的电压-频率曲线

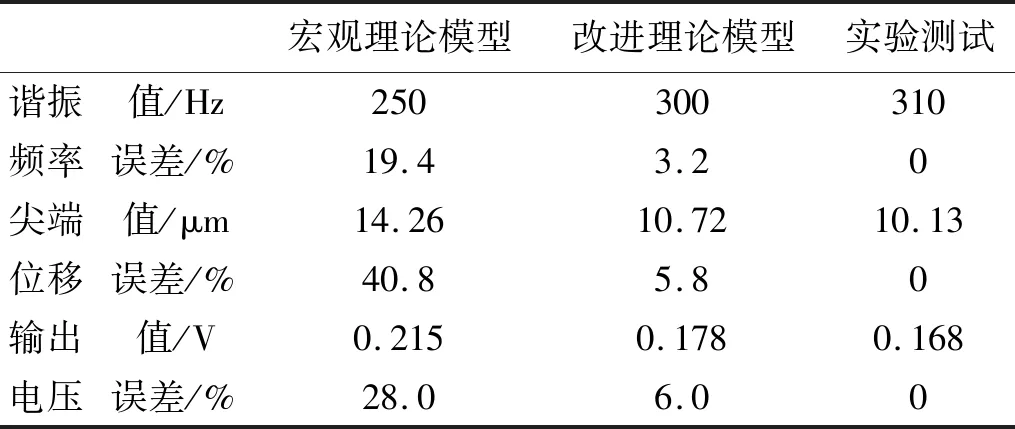
宏观理论模型改进理论模型实验测试谐振值/Hz250300310频率误差/%19.43.20尖端值/μm14.2610.7210.13位移误差/%40.85.80输出值/V0.2150.1780.168电压误差/%28.06.00

宏观理论模型分析与实验测试获得的谐振频率之间误差为19.4%，尖端位移误差为40.8%，输出电压误差为28%，宏观模型无法准确描述微振动能量采集器的动力学性能；改进理论模型分析与实验测试两种方式获得的谐振频率之间误差为3.2%，尖端位移误差为5.8%，输出电压的误差为6.0%，改进模型分析的结果与实验结果吻合较好，但仍有一定误差。

3 误差影响因素分析

理论计算与实际测试结果之间的偏差，可由两方面的因素导致：一是在理论模型中存在一些近似假设，例如Euler梁[21]假设，一是计算参数不够精确。

在理论建模方面，如前所述，尺度效应是理论模型误差的一个重要来源，此外应考虑其他理论假设因素的影响。由于本文理论计算是基于有限元模型，在建模方法上是将压电层和Si基梁分别划分相同数量的单元，在两种材料的结合面上令其对应单元节点合二为一，其中即考虑了材料剪切作用的影响，因此可以认为理论模型本身有较高的计算精度。

由于微器件的加工制作公差，使计算参数不够精确，不可避免地造成理论计算与实际测试结果之间的偏差。以下仅以式(1)的Euler梁模型对加工公差造成的计算误差进行简要分析。在此采用Euler梁模型一方面是为简化理论计算，一方面注意到对于本文算例，压电层的厚度远小于Si基梁，PZT-5H的杨氏模量也远小于Si，按设计尺寸，可估算压电层与Si基梁的抗弯刚度之比约为5.2×105。

在式(3)中令r=1，并注意到β1L=1.875以及对矩形截面I=Ah2/12，同时引用式(4)的等效杨氏模量，有

(8)

显然，根据式(8)，微梁宽度误差不对其基频产生影响。假设微梁的长度存在加工误差ΔL，则由其导致基频计算误差

(9)

取式(9)与式(8)的比值

(10)

亦即每1%的长度加工误差将导致约2%的固有频率计算误差。类似地可知，每1%的厚度加工误差将产生相同比率的固有频率计算误差。此外，设若材料密度取值与实际值存在1%的偏差，则导致固有频率计算产生约0.5%的误差。最后，基于Euler梁理论也可对尺度效应造成的固有频率计算误差进行大致估计

(11)

对本文算例，式(11)计算结果约为18.8%，对比表2的宏观理论模型误差大致相当；上式计算结果偏大的主要原因，可解释为ΔE1较大，因而需要考虑泰勒级数的高阶项以提高误差估计精度。

4 结 论

本文以微压电悬臂梁为研究对象，研究了尺度效应对微结构力学性能的影响，引入材料的本征长度，采用改进的偶应力理论完善了动力学模型。通过有限元分析与实验测试的方式研究了微压电悬臂梁的力学性能，表明改进模型精度更高。以微梁力学性能研究结果为基础，改进了微振动能量采集器的动力学模型，采用有限元方法和实验测试分析采集器的输出性能。改进的采集器动力学模型可以更好的解释尺度效应对微结构力学性能的影响。