碾压混凝土HJC动态本构模型修正及数值验证

2019-07-08张社荣魏培勇

振动与冲击 2019年12期

张社荣，宋冉，王超，尚超，魏培勇

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300350；2. 天津大学建筑工程学院，天津 30035)

随着碾压混凝土在水工大坝建设中的应用越来越广，需要考虑结构可能遭受到地震、爆炸等极端荷载的作用。目前对水工大坝结构的抗震研究还局限在将材料的静态力学特性参数提高一定比例的方式上，抗爆研究更是缺乏统一的标准[1-3]，因此有必要对碾压混凝土的动态力学特性进行深入的研究。碾压混凝土作为一种组分复杂、施工成型方式明显区别于常态混凝土的材料，采用何种本构模型描述其在冲击荷载下的动态力学行为是一个值得探讨的问题[4]。国内外学者针对混凝土类材料动态本构理论进行研究，获得了多种关于承受冲击、爆炸等动力荷载下率相关的混凝土动态本构模型，例如基于黏弹性理论建立的粘弹性动态本构模型(ZWT模型)[5]、基于黏塑性力学理论的粘塑性本构模型[6]，以及考虑静水压力、应变率强化效应和应变软化的影响的本构模型[7]，如Holmquist-Johnson-Cook(HJC)模型、连续光滑盖帽(CSC)模型和Karagozian&Case(K&C)模型等。其中HJC本构模型[8]是针对混凝土材料在大应变、高应变率、高压下提出的一种率相关的动态损伤本构模型，适合描述材料在压缩状态下的损伤规律。巫绪涛等[9]基于LS-DYNA有限元计算程序，采用HJC本构模型对混凝土的SHPB试验进行了模拟，得到了和试验结果一致的力学行为；吴赛等[10]通过模拟混凝土的SHPB试验，得到了HJC模型中各关键参数对混凝土动态力学性能的影响规律，由此对模型的原始参数进行了修正；任根茂等[11]以常态混凝土的静态单轴压缩试验、三轴压缩试验、SHPB试验和飞片撞击Hugoniot试验结果为依据，确定了一套适用于常态混凝土的HJC模型参数，并用于混凝土靶板冲击试验的模拟中；Kong等[12]不仅对混凝土HJC模型中的强度面参数和应变率效应进行了修正，还重新考虑了罗德角和拉伸损伤的影响，利用修正后的HJC模型模拟了混凝土靶板冲击试验中的开坑和碎甲效果，与试验结果吻合良好。上述研究均针对常态混凝土，对于碾压混凝土动态本构模型的确定及其适用性目前几乎处于空白，因此本文就碾压混凝土开展了准静态单轴压缩试验和SHPB试验，并借助已有文献中的碾压混凝土三轴压缩试验成果，对HJC模型中的强度面参数和应变率增强效应进行修正，给出修正模型参数的确定方法，基于有限元计算程序建立SHPB试验的数值模型，验证修正HJC模型描述碾压混凝土在冲击荷载下动态力学特性的有效性。

1 模型修正的试验基础

1.1 试验概述

参考黄登水电站碾压混凝土大坝施工实际的材料配比和成型方式进行试样的制备，主供材料如下：水泥(祥云中热42.5号硅酸盐水泥)，粉煤灰(贵州火焰Ⅱ级)，河砂，人造粗骨料(粒径5～12 mm)，减水剂(江苏博特JM-IIRCC)和引气剂(云南晨磊HLAE)。使用DC-25C手持式压路机对混凝土拌合料分层摊铺碾压，每层厚10 cm，共计5层。制备了强度等级分别为C15和C20的碾压混凝土试样，在温度为33℃和相对湿度为95%的条件下养护90天，之后进行钻取、切割、打磨得到∅100 mm×200 mm、∅70 mm×35 mm和∅50 mm×25 mm的圆柱体试样。表1为两种强度碾压混凝土试样的配合比，图1为试样制备和成型过程。

表1 碾压混凝土试样的配合比

图1 碾压混凝土试样成型过程

分别对制备的碾压混凝土试样进行准静态单轴压缩试验和SHPB冲击试验。受试验条件限制，准静态三轴压缩试验数据参考已有文献中的结果。采用天津大学水利工程实验室的微机控制电液伺服加载试验机对碾压混凝土试样(∅100 mm×200 mm)进行单轴压缩试验，加载应变率为10-5s-1，试验结果取三个试样加载结果的平均值。动态冲击试验采用中南大学研制的利用异形冲头作为整形方法的杆径分别为75 mm和50 mm的SHPB装置，对∅70 mm×35 mm和∅50 mm×25 mm两种尺寸的碾压混凝土试样进行了应变率范围为50～150 s-1的冲击压缩试验。

1.2 准静态压缩试验结果

经试验测定，C15碾压混凝土试样的准静态单轴压缩强度为16.4 MPa，C20试样的准静态单轴压缩强度为20.9 MPa。

静载下三轴压缩试验参考邓荣贵等[15]的研究，采用MTS815TestStar数字程控伺服岩石力学刚性试验机进行加载，控制加载应变速率为10-5s-1，试验结果如表2所示。由表2的结果可以看出，碾压混凝土的峰值压缩强度和残余强度均随围岩的增大而增加。

1.3 SHPB试验结果

通过调节加载压力控制SHPB试验中异型冲头的冲击速度从而控制加载波形的峰值。图2给出了不同尺寸和强度碾压混凝土试样的应力-应变曲线。可以看出，C20碾压混凝土试样的动态峰值应力大于C15，峰值应力对应的应变在近似应变率加载下差别不大。在平均加载应变率为91 s-1和136 s-1时，C20试样的峰值强度分别比准静态单轴抗压强度高54%和126%。C15试样在平均应变率98 s-1和147 s-1下的峰值强度分别比准静态单轴抗压强度高127%和170%，说明强度低的试样在高应变率加载下的应变率增强效应更为明显。从图2(a)和图2(c)所示的两种尺寸的C20试样的应力-应变关系可以看出，在加载波形峰值为175 MPa时，∅50 mm试样的平均应变率达到136 s-1，大于∅70 mm的96 s-1，说明大直径的碾压混凝土试样强度较低、更易破坏。

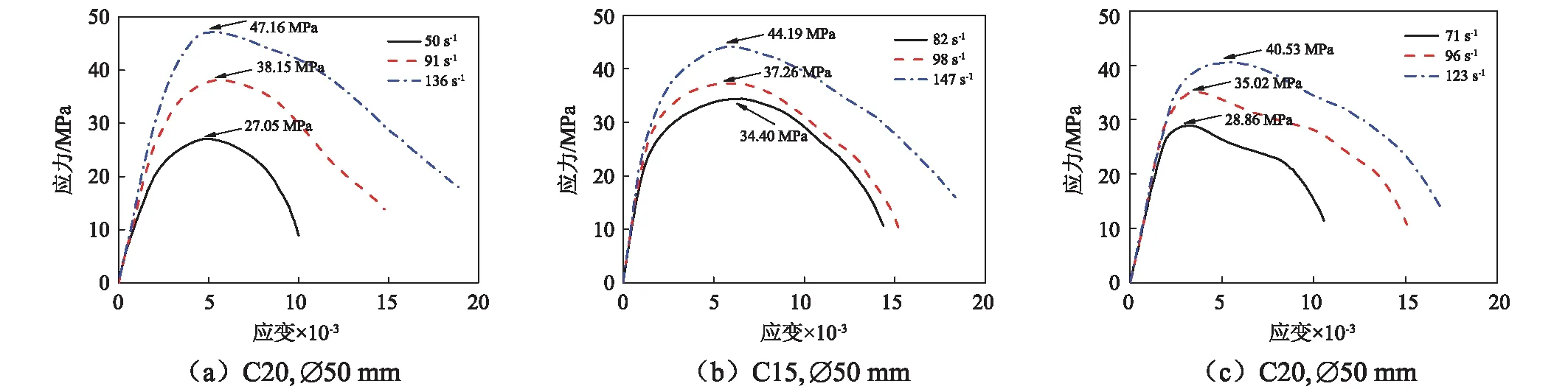
图2 碾压混凝土SHPB试验应力-应变曲线

2 HJC本构模型修正

2.1 原始HJC本构模型

参考对碾压混凝土的HJC动态本构模型进行修正前，首先对原始的HJC模型进行简要介绍，主要包括屈服面方程，损伤方程和静水压力随体积应变的变化关系，如图3所示。

HJC模型屈服面方程(图3(a)所示)由式表示：

(1)

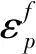
图3 原始的HJC模型

图3(c)所示为混凝土材料所受静水压力和体积应变的关系。OA段为线性关系，ppl，材料内不再存在孔隙并被彻底压碎。各阶段加、卸载过程的表达式可参考Holmquist等的研究结果。图中pc和μc分别为单轴压缩试验中的压碎压力和相应的体积应变；pl和μl为锁定压力和相应的锁定体积。

HJC模型目前常被用于描述常态混凝土的动态力学特性，虽然碾压混凝土在成型方法和材料配比上与常态混凝土有所不同，但考虑到两类材料的各项力学参数相近，可依据试验数据就原始HJC模型进行针对于碾压混凝土的修正。从前述HJC模型包含的方程可知，强度屈服面可由三轴压缩试验数据确定，动态抗压强度的应变率增强效应由SHPB试验结果确定。

2.2 强度面修正

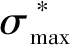
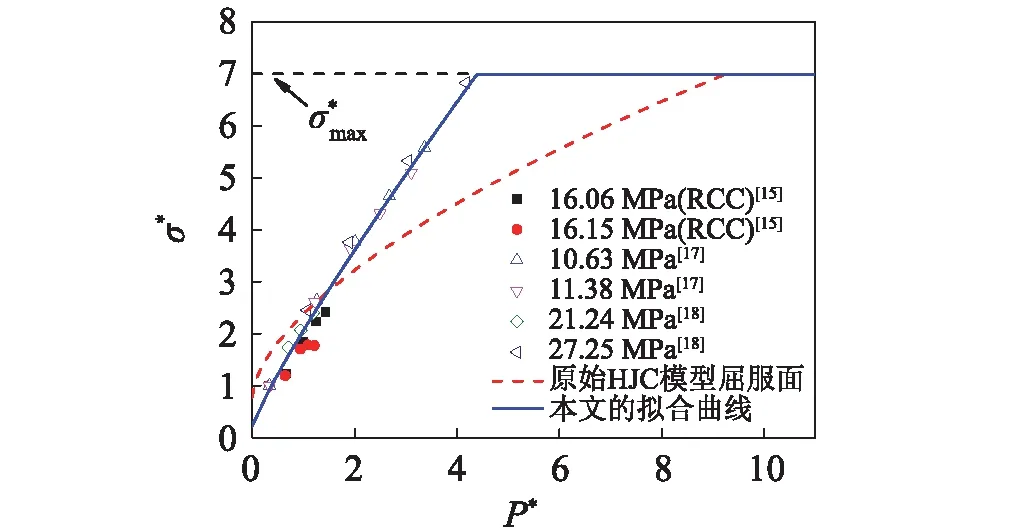
图4 基于三轴压缩试验结果的强度面修正

(2)

2.3 应变率增强效应修正

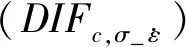
(3)

式中:DIFσ,t为抗拉强度增长因子，ft为单轴抗拉强度。

图5给出了DIFc,σ(动态压缩强度增长因子)随应变率的关系，包括CEB(Comite Euro-International du Beton)模型[19]、常态混凝土的试验结果[20]和碾压混凝土试验结果[21]。其中LI和Meng的研究结果消除了惯性效应的影响，因此DIFc,σ明显低于CEB模型的计算值，式给出了根据本文碾压混凝土SHPB试验数据并按照Li和Meng的研究结果减去惯性效应影响后的动态强度增长因子DIFc,σ并用于修正的HJC模型中，应变率参数C取为0.315。

(4)

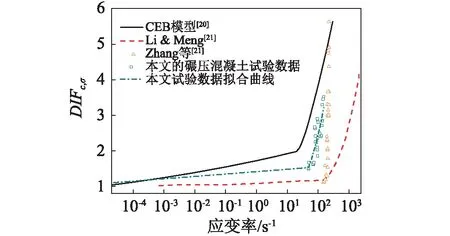
图5 基于试验数据和经验公式的DIF

2.4 模型参数确定

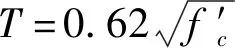
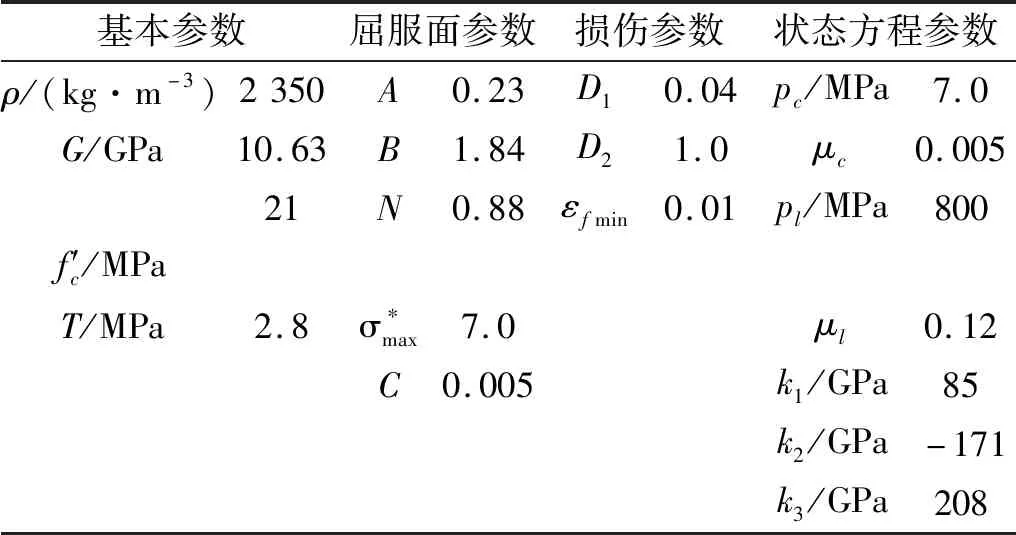
表3 C20碾压混凝土的修正HJC模型参数

3 修正HJC模型的数值验证

3.1 SHPB试验的数值模型

为了评估前述修正HJC模型对描述碾压混凝土在冲击荷载作用下的动态力学响应特性，借助有限元分析手段，对50 mm杆径的SHPB试验进行模拟。图6为SHPB数值试验的模型图。计算模型包括入射杆、碾压混凝土试样和透射杆三部分，其中入射杆和透射杆长度均为2.0 m，压杆材料为高强钢，密度为7 800 kg/m3，弹性模量200 GPa，泊松比取0.25，与SHPB试验相同，在两杆中部表面布设典型的应变测点。考虑到模型对称性，计算采用1/4建模，模型的互相垂直的两端面施加无反射边界。采用在入射杆前端面加载一定压力峰值(对应试验加载的几种应变率，分别为75 MPa、125 MPa和175 MPa)的半正弦波形以获得异形冲头整形后的加载效果，压杆/试样接触面采用“侵蚀面面接触”算法，经试算后，压杆网格尺寸约为0.005 m，试样网格尺寸为0.001 25 m。SHPB试验中采用的碾压混凝土试样，其高度均小于成型过程中单层摊铺料的厚度，大部分试验用试样并未包含施工层面，模拟计算中亦不予考虑，且不考虑碾压混凝土材料的细观结构，按照均质材料计算，材料采用表2给出的修正HJC模型参数。为合理描述碾压混凝土的损伤破坏，并结合SHPB试验过程中高速摄像机拍摄到的试样破坏过程[22]，采用最大主应变破坏准则，即ε1≥εmax时，模型中的单元失效并被删除，同时失去承载能力，其中ε1最大主应变，εmax为破坏时的最大主应变。

3.2 应力-应变关系重构

对C20强度等级的∅50 mm碾压混凝土试样的SHPB试验进行模拟计算，根据得到的典型测点1#、2#的应变时程曲线，按照“三波法”重构可得到碾压混凝土试样的应力-应变曲线，并与试验结果进行对比，如图7所示。其中实线为试验曲线，虚线为模拟计算得到的结果，且分别对应模拟加载正弦压力波峰值75 MPa、125 MPa和175 MPa的工况。

(a) SHPB试验系统及测点布置

(b) 模型局部放大示意图

图7所示的碾压混凝土试样应力-应变关系与1.3节中的试验结果基本一致，试样强度随加载应变率的提高而增大，试样严重破坏阶段的曲线曲率随应变率的增大而有所减小，说明损伤演化程度更加充分。对比SHPB试验结果的应力-应变关系曲线和数值计算结果可知，采用修正的HJC本构模型参数可准确有效地重现碾压混凝土在冲击压缩荷载作用下的动态力学特性。

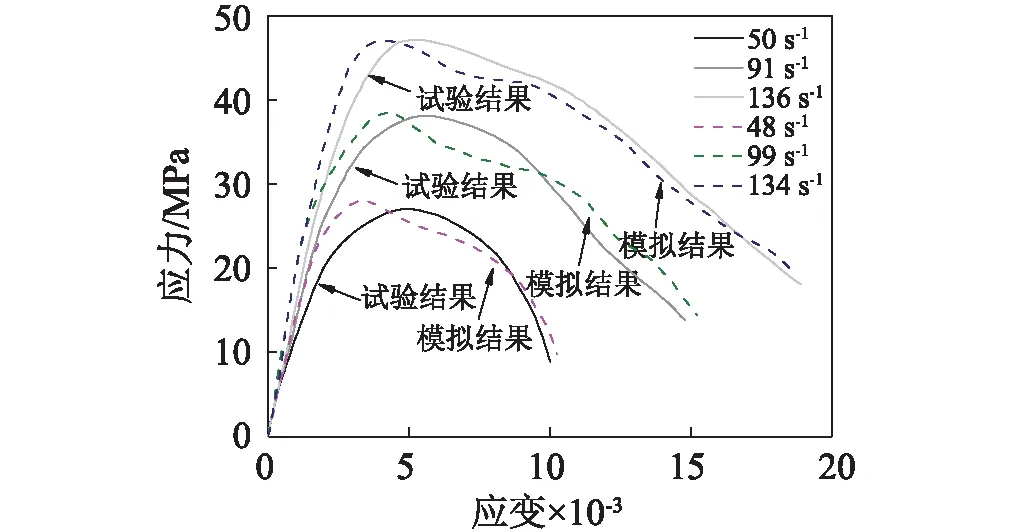
图7 不同应变率下碾压混凝土应力-应变曲线

3.3 试样破坏模式

失效准则的选取对于描述结构破坏模式和冲击荷载作用下损伤破坏阶段的动态响应至关重要，在数值计算中采用不同的失效准则(最大主应变失效准则和切应变失效准则)得到的试样破坏模式往往差异明显。图8给出了平均加载应变率为48 s-1时不同失效准则的计算结果，并与试验结果[16]进行了对比。由试验结果可知试样的破坏呈现出留核现象，破坏表现为从四周到中心的发展过程，采用最大主应变失效准则，且εmax=0.05时对碾压混凝土受冲击压缩荷载时的行为进行模拟最为接近试验结果。