饱和土-管桩-刚性承台水平振动研究
2019-07-08刘林超闫启方
刘林超, 闫启方
(信阳师范学院 建筑与土木工程学院,河南 信阳 464000)
桩基振动特性的研究一直是岩土工程和地震工程领域研究的重点[1-5],近年来管桩作为一种新型桩在建筑工程、海洋工程、高速铁路工程等众多领域得到了广泛应用,由于管桩经常要承受诸如地震、海浪等动态激励的作用,所以针对管桩在动态荷载作用下力学特性的研究近年来得到了足够的重视,并取得了一定的研究成果,如丁选明等[6]考虑土体材料的黏性阻尼和桩-土纵向耦合振动,采用Laplace变换的方法求得了轴对称均匀黏弹性地基中现浇薄壁管桩纵向振动的解析解,郑长杰等[7-9]从土体三维波动方程出发,对黏弹性和饱和黏性土地基中管桩水平振动响应以及横观各向同性饱和土中管桩的扭转振动进行了理论研究,刘林超等[10]将桩周土、桩芯土和管桩视为一个整体,利用轴对称模型和桩-土接触面的连续性条件得到了管桩的竖向振动解,靳建明等[11]基于Biot饱和多孔介质的波动方程,研究了均质各向同性饱和土中端承管桩的扭转振动。当前针对管桩的研究主要是研究完全埋入管桩,且假定管桩深度和管桩桩身长度相等,不考虑管桩桩顶承台或结构的影响。考虑桩顶承台或上部结构影响研究管桩动态响应的研究相对较少,相关的研究主要针对实芯桩,黄茂松等[12]运用简化解析方法对部分埋入群桩基础的水平-摇摆耦合振动和基础阻抗对风机结构共振特性的影响进行了研究,朱超等[13]通过振动台模型试验得到了软夹层地基上土-桩-隔震结构动力相互作用体系的振动反应特性及其规律,邵艳丽等[14]基于桩-土相互作用的Winkler模型,将桩等效为Timoshenko梁,上部结构等效为单自由度弹簧质量块,研究了垂直入射简谐SH波作用下桩-液化土-上部结构耦合体系的水平振动特性。由于管桩的广泛应用和动态激励的作用,而以往的研究主要以单个管桩为研究对象,较少开展管桩-承台或管桩-上部结构耦合体系动态响应的研究,开展管桩-承台或上部结构耦合体系的振动研究对于管桩-结构的抗震设计、施工等具有十分重要的理论和实际工程应用价值,同时我国长江三角洲、珠江三角洲等地区存在大量的饱和土,有必要进行饱和土-管桩-刚性承台的动态响应研究。本文将基于多孔介质理论,研究饱和土-管桩-刚性承台耦合体系在水平简谐荷载作用下的动态响应。
1 系统模型与基本方程
1.1 模型与假定
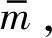
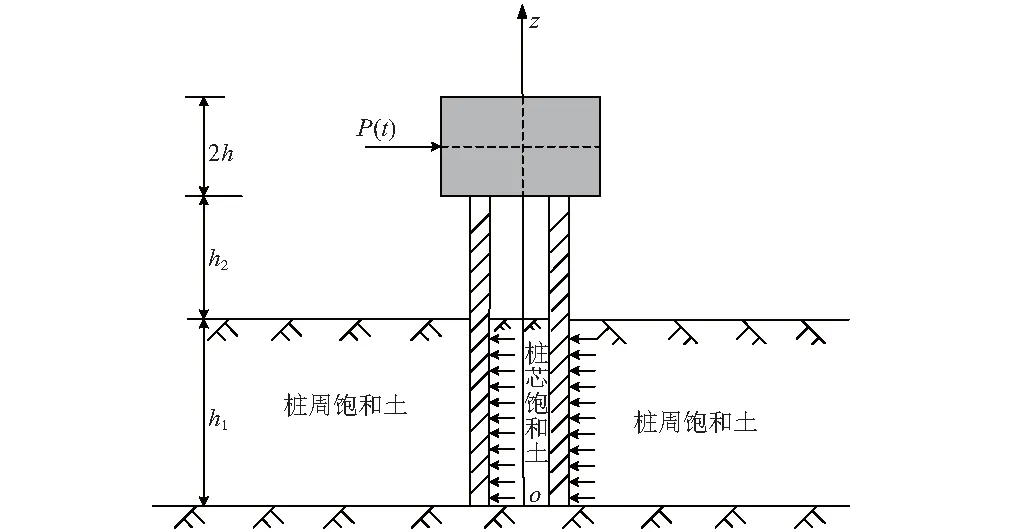
图1 饱和土-管桩-刚性承台模型
1.2 桩周饱和土和桩芯饱和土运动方程
基于多孔介质理论可以建立桩周饱和土和桩芯饱和土的控制方程为[15]
(1)
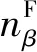
1.3 刚性承台运动方程
(2)
(3)

1.4 边界条件与连续性条件
桩周饱和土无限远处位移满足
(4)
设桩周饱和土与管桩、桩芯饱和土与管桩接触面不透水,满足
(5)
管桩与桩周饱和土、管桩与桩芯饱和土接触面处位移满足连续性边界条件
(6)
和
(7)
式中:u1p为埋入部分管桩的水平位移,这里假设管桩与土下基岩完全接触,即管桩为端承摩擦桩,则管桩埋入部分、外露部分满足如下边界条件和连续性边界条件
(8)
2 桩周饱和土和桩芯饱和土运动方程求解
为了求解问题,需要求解出桩周饱和土和桩芯饱和土的水平振动,参考文献[16]通过引入势函数的方法,在忽略竖向位移和轴对称坐标下对桩周饱和土和桩芯饱和土的水平振动进行解耦和求解,考虑饱和土的位移边界条件求出桩周饱和土和桩芯饱和土的径向和环向位移,随后根据应力和位移关系可以得到单位厚度桩芯土和桩周土对管桩的作用力,再利用初始参数法和传递矩阵法求解管桩和承台的振动进而得到承台的水平位移。
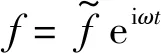
(9)
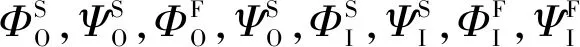
桩周饱和土
(10)
桩芯饱和土
(11)
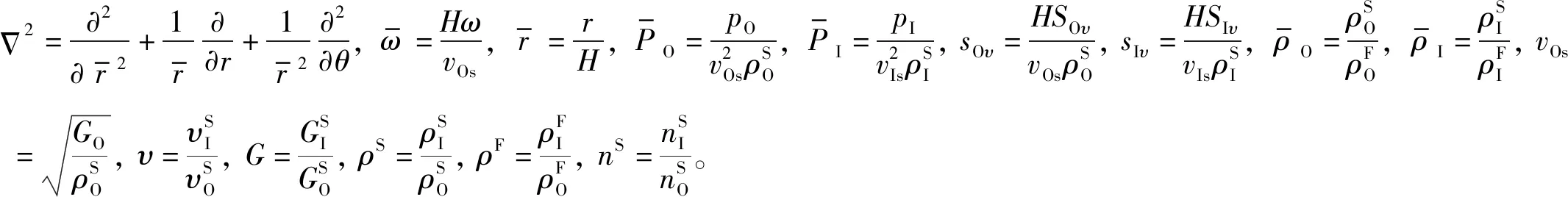
考虑式(4)和式(5),求解式(10)和式(11)可得势函数和孔隙水压力分别为
(12)
(13)
(14)
(15)
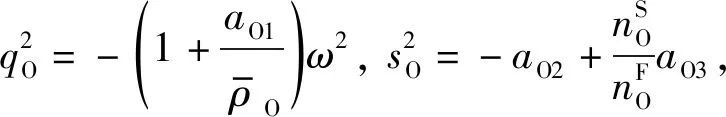

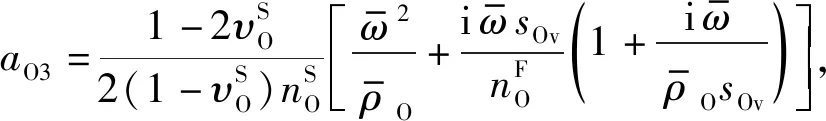

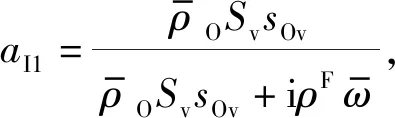

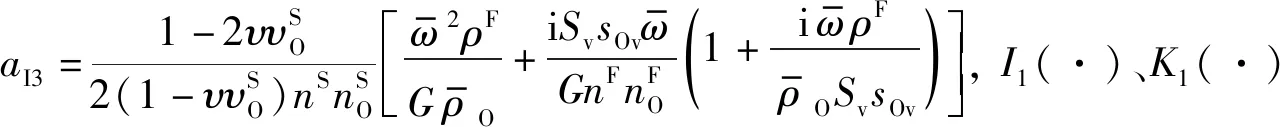
(16)
(17)
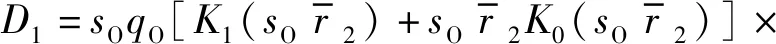
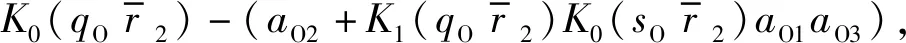

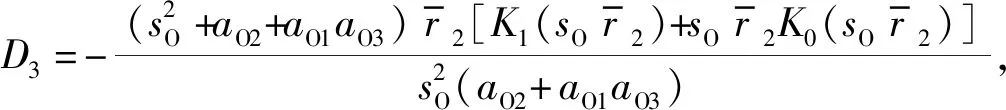

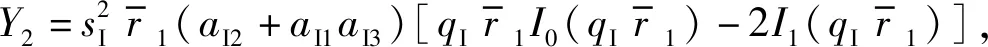
由式(12)~式(15)和式(9)可以求出桩周饱和土和桩芯饱和土的径向位移和环向位移,再根据应力位移关系可以得到桩周饱和土和桩芯饱和土的径向应力和剪切应力,进而可以得到当管桩产生单位水平位移时单位厚度桩周饱和土和桩芯饱和土对管桩的无量纲化后的水平作用力分别为
FO=πfO,FI=πfI
(18)
式中:
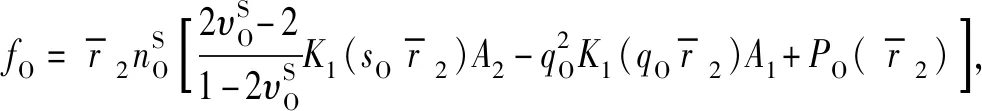
3 饱和土-管桩-承台系统运动方程求解
考虑桩周饱和土和桩芯饱和土对管桩的作用式(18),可以建立无量纲化后的埋入部分管桩和外露部分管桩的运动方程为
(19)
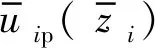
运用初参数法求解方程式(19)可得[17]
(20)
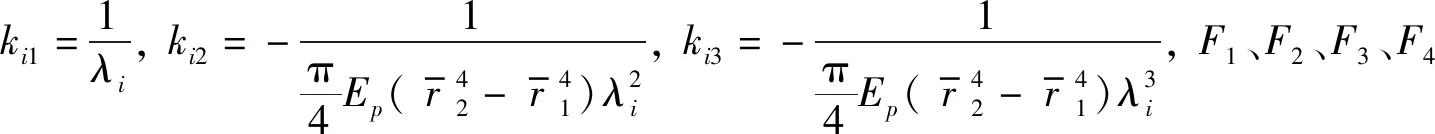
(21)
分别以各部分管桩桩底为坐标原点建立坐标系,由式(20)和式(21)可得埋入部分管桩和外露部分管桩的桩顶和桩底位移、转角、剪力和弯矩之间的关系为
(22)
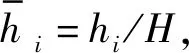
[T]i=
(23)
以整个管桩的桩底为坐标原点建立坐标系,考虑埋入部分管桩和外露部分管桩的连续性边界条件式(8)的第2式,运用矩阵传递法[18]可以建立外露部分管桩桩底与埋入部分管桩桩底的关系,即
(24)
这里,
(25)
假设管桩桩底完全固定,桩底位移和转角为零,由式(8)的第1式边界条件得
(26)
由于刚性承台也做简谐振动,消去式(2)和式(3)各参量的eiωt项,并进行无量纲运算则有
(27)
(28)
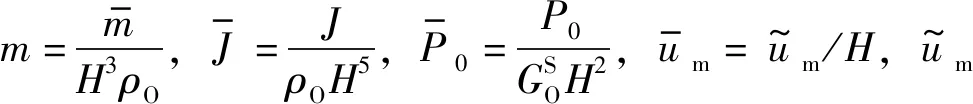
(29)
(30)
由式(29)和式(30)可得
(31)
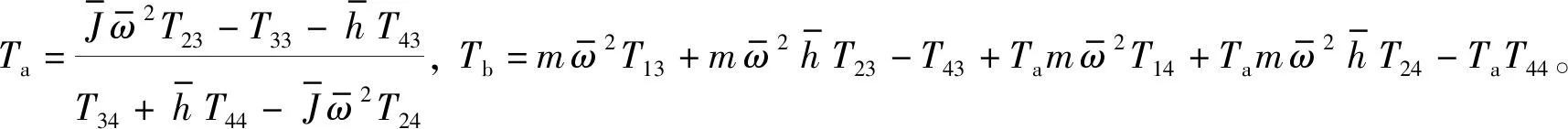
(32)
4 数值分析与讨论
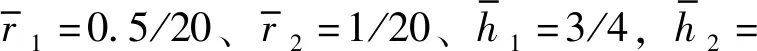
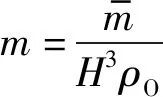
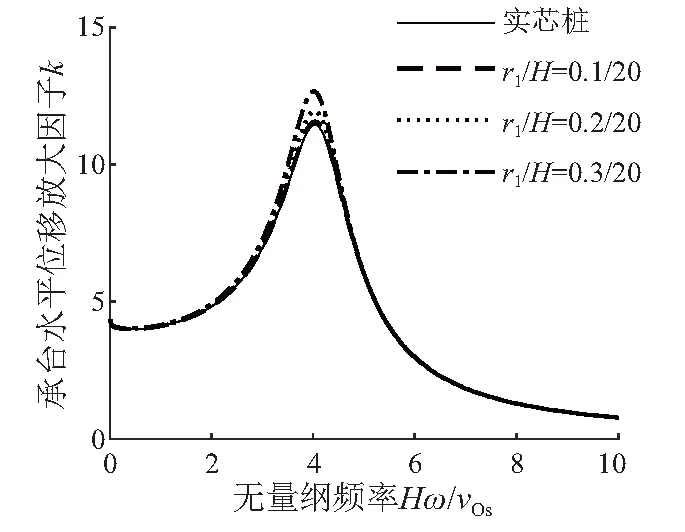
图2 桩芯半径不同时位移放大因子随频率变化曲线
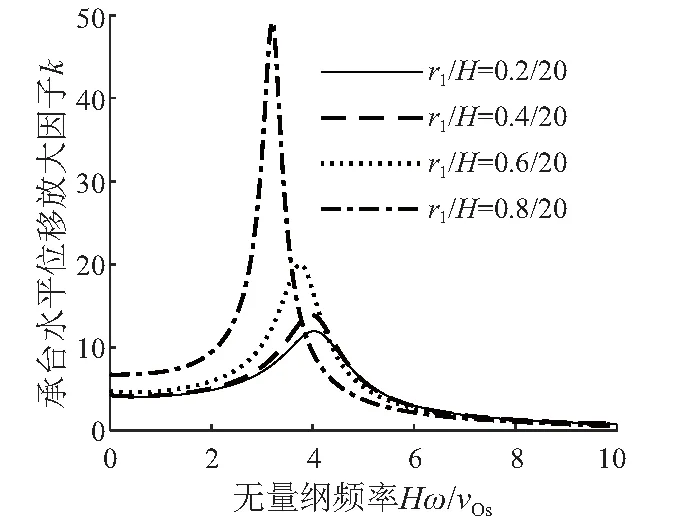
图3 桩芯半径不同时位移放大因子随频率变化曲线
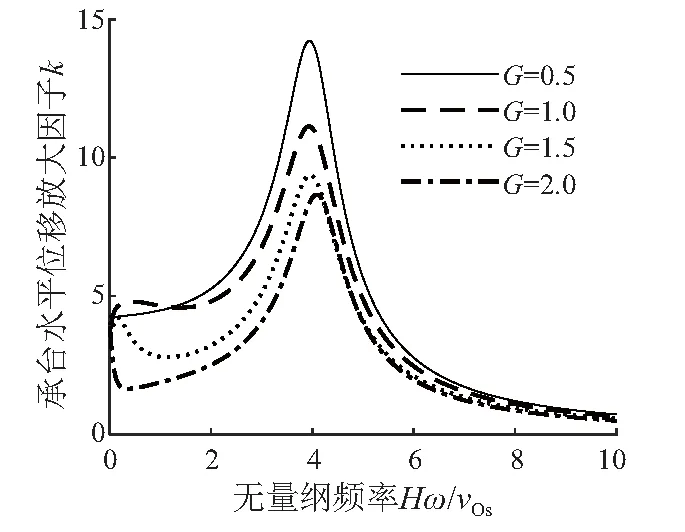
图4 桩芯与桩周饱和土固相剪切模量比不同时位移放大因子随频率变化曲线
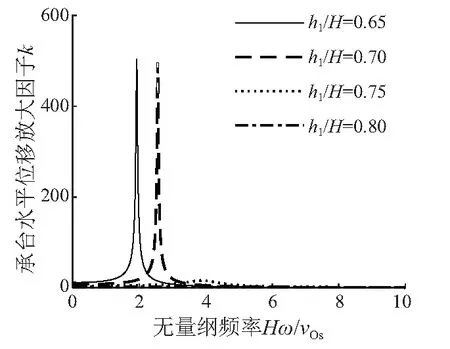
图5 管桩外露部分长度不同时位移放大因子随频率变化曲线

图6 承台高度不同时位移放大因子随频率变化曲线

图7 承台质量不同时位移放大因子随频率变化曲线
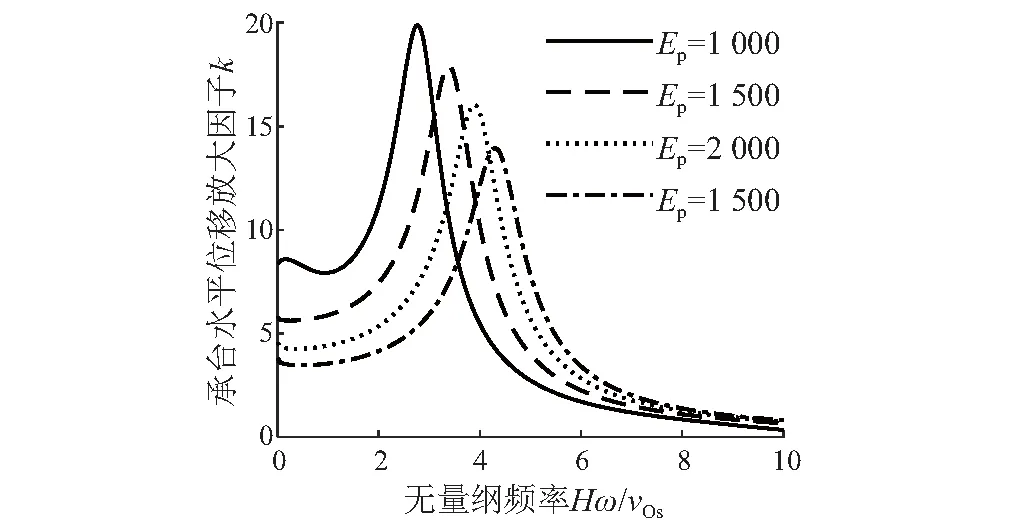
图8 管桩与桩周饱和土模量比不同时位移放大因子随频率变化曲线
5 结 论
本文以饱和土-管桩-刚性承台耦合体系为研究对象,借助于初始参数法和传递矩阵法,在考虑边界条件和连续性条件的情况下得到了水平简谐荷载作用下刚性承台水平位移的解析解,最后进行了数值算例分析,主要得到以下结论:
(1) 在水平简谐动态激励作用下需要考虑饱和土-管桩-刚性承台耦合体系的共振,工程设计中应使体系周期避开荷载周期。
(2) 管桩桩壁不宜过薄,否则容易产生共振而导致位移幅值过大。
(3) 虽然实际工程施工中管桩经常不被充满,但将桩芯土填满并夯实以及管桩埋入部分越长可以较明显的降低刚性承台的水平位移幅值,对提高结构体系的抗震有利。
(4) 在设计中建议在允许的情况下降低承台高度和重量。
