基于本征正交分解的波浪力随机场降维模拟

刘章军， 刘 磊， 汪 峰

(1. 武汉工程大学 土木工程与建筑学院，武汉 430074；2. 三峡大学 土木与建筑学院，湖北 宜昌 443002)

随着我国经济快速发展，海洋资源的开发日益重要，对海洋工程结构(如海上平台、离岸码头和海上风电机装置等)安全性的要求越来越高。此类结构下部支撑一般为墩柱结构，在复杂的海洋环境中，将受到波浪荷载、风荷载、轮渡撞击和地震等作用。其中，波浪荷载是主要作用力之一，其不仅随时间变化(具有动态特性)，而且具有明显的随机性和空间相干性，因而采用波浪力随机场加以描述[1]。

在波浪随机过程或随机场研究中，Pierson[2]建立了波面位移随机过程与波高谱之间的关系，开辟了应用波高谱研究波浪随机过程的先河。Borgman[3]对Morison方程进行了线性化处理，并利用谱分析法研究了作用在柱桩上的随机波浪力。Di Paola等[4]结合波高与波速的关系，利用本征正交分解(POD)方法模拟了波速随机场。Ren等[5]进行了结构在随机波浪冲击下的数值模拟分析，并与实验数据进行对比。Dong等[6]结合波浪谱模拟了重力式网箱在随机海浪力作用下的力学特性。上述方法均是基于波高谱来实现波浪随机过程或随机场模拟。在波浪方向谱研究方面，Longuet-higgins等[7]应用傅里叶级数估计海浪方向谱，并提出了方向谱的分布函数。Ren等[8]对方向谱的观测方法进行了改进，并进行了波面模拟；文献[9-11]利用方向谱对波浪进行了三维数值模拟；赵振民等[12]则将波面的三维仿真模拟用于船舶振动研究。

上述波浪随机过程或随机场模拟均是以Monte Carlo方法为基础，为保证模拟精度，往往需要对一系列随机变量进行大量的随机抽样，不仅极大地增加了波浪随机场模拟的计算量，而且对复杂海洋工程结构的非线性随机动力反应分析带来巨大困难。为克服这一困难，文献[13-14]通过引入随机函数的约束，实现了仅用一个基本随机变量即可精确地模拟一维单变量随机过程。为此，本文将随机函数思想引入到平稳多变量随机过程模拟的POD方法中，结合线性化的Morison方程和P-M波浪谱，实现用两个基本随机变量即可模拟作用于小尺度桩上的波浪力随机场，且仅需数百条代表性样本即可在概率密度层次上描述波浪力随机场的概率特性，为结合概率密度演化理论[15-16]研究海洋工程结构在随机波浪力场作用下的动力响应与可靠度分析奠定基础。

1 基于正交随机变量的本征正交分解

本征正交分解是时-空随机场模拟的最主要方法之一。在一般情况下，由于无法直接获取特征问题的解析解或封闭解，需要将连续的1V-2D时-空随机场f0(x,t)离散化为nV-1D随机过程X(t)。

假设X(t)=[X1(t),X2(t),…,Xn(t)]T是一个零均值的nV-1D平稳随机过程，其双边的功率谱密度函数矩阵SX(ω)可表示为

(1)

式中：Sii(ω)是第i个分量过程Xi(t)的自功率谱密度函数；Sij(ω)(i≠j)是第i个分量过程Xi(t)与第j个分量过程Xj(t)的互功率谱密度函数。

一般地，功率谱密度函数矩阵SX(ω)是一个非负定的Hermitian矩阵， 其特征值λi(ω)是频率ω的非负实函数， 特征向量ψi(ω)=[φ1i(ω),φ2i(ω),…,φni(ω)]T一般是频率ω的复函数。对于任意给定的频率ω，存在如下的特征问题

Ψ*T(ω)Ψ(ω)=In×n,SX(ω)Ψ(ω)=Ψ(ω)Λ(ω)

(2)

式中： 符号“*”和“T”分别表示共轭和转置；Λ(ω)=diag{λ1(ω),λ2(ω),…,λn(ω)}为特征值矩阵；Ψ(ω)=[ψ1(ω),ψ2(ω),…,ψn(ω)]为特征函数矩阵。

对于零均值的nV-1D平稳随机过程X(t)， 可分解为n个互不相干的子随机向量过程之和[17]

(3)

式中： 子随机向量过程xi(t)的表达式为

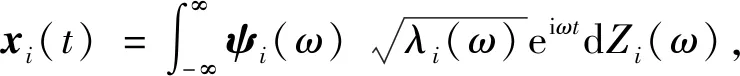
(4)

在式(4)中，Zi(ω)(i=1,2,…,n)是零均值的复随机过程，其增量满足如下的基本条件

E[dZi(ω)]=0

(5a)

(5b)

(5c)

式中：δij和δωω′均为Kronecker符号。

进一步地，在式(4)中，若令

(6)

式中：Pik是一组零均值的标准正交复随机变量，满足如下的基本条件

(7)

于是，子随机向量过程xi(t)可近似地表达为有限级数的复形式

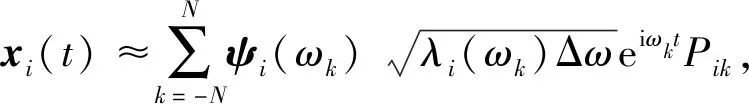
(8)

式中：ωk为离散的频率点，N为频率截断项数， Δω为频率步长。为了尽量避免零频率点对模拟结果的影响，本文定义ωk如下

(9)

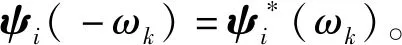
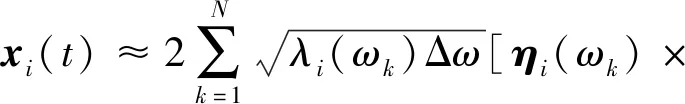
(10)

式中：Rik和Iik是一组零均值的正交随机变量，满足如下的基本条件

E[Rik]=E[Iik]=0

(11a)

E[RikIjm]=0

(11b)

(11c)

最后，将式(10)代入式(3)中得到平稳多变量随机过程X(t)的本征正交分解

(12)

式(12)即为基于正交随机变量的本征正交分解。 在实际应用中，由于正交随机变量Rik和Iik仅需满足基本条件式(11)， 其概率分布并未给定，因而不能直接采用式(12)来模拟平稳多变量随机过程。

2 基于本征正交分解的降维模拟

在基于正交随机变量的本征正交分解式(12)中，若将正交随机变量Rik和Iik定义为

Rik=cosφik,Iik=sinφik

(13)

式中：φik(i=1,2,…,n,k=1,2,…,N)为区间[0,2π)上相互独立的均匀分布随机相位角。显然，式(13)满足正交随机变量的基本条件式(11)。

同时，将特征向量ψi(ωk)的实部ηi(ωk)和虚部ρi(ωk)分别写为

ηi(ωk)=|ψi(ωk)|cos ϑi(ωk)

(14a)

ρi(ωk)=|ψi(ωk)|sin ϑi(ωk)

(14b)

于是，将式(13)和式(14)代入式(12)中，得到基于随机相位角的本征正交分解模拟式[18]

(15)

式中：X(C)(t)为传统的本征正交分解模拟过程。在式(15)中，由于随机相位角的概率分布已知，通过随机相位角的一组随机抽样即可生成样本函数，因而在工程模拟中得到广泛应用。

从上述式(15)的推导过程可知，基于随机相位角的本征正交分解式(15)是基于正交随机变量的本征正交分解式(12)的一个特例。事实上，通过定义正交随机变量Rik和Iik为式(13)的形式，使得式(15)中随机变量的数量比式(12)减少一半。这表明，通过施加某种约束(即定义式(13))可以有效地减少平稳随机向量过程模拟的随机度(随机变量的数量)。

进一步，在基于正交随机变量的本征正交分解式(12)中，可利用随机函数对正交随机变量Rik和Iik施加更强的约束，从而实现平稳随机向量过程的降维模拟。为此，将满足基本条件式(11)的正交随机变量Rik和Iik均定义为r维随机变量Θ=(Θ1,Θ2,…,Θr)的正交函数形式， 即Rik=hik(Θ)，Iik=gik(Θ)， 其中hik(·)和gik(·)均为确定性的正交函数。于是，式(11)可改写为

(16a)

(16b)

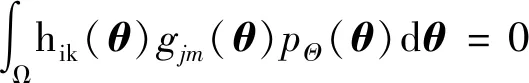
(16c)

(16d)

(16e)

式中：i,j=1,2,…,n和k,m=1,2,…,N；Ω为r维随机变量Θ的定义区间；pΘ(θ)为r维随机向量Θ的联合概率密度。

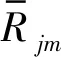
(17)

3 基于线性化Morison方程的波浪力随机场

在随机波浪下，水质点的水平速度u和水平加速度a可分别表示为

(18)

(19)

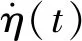
ω2=gktanh (kh)

(20)

式中：g为重力加速度，可取g=9.81 m/s2。

对于直立的小直径圆柱桩，可采用Morison公式来计算随机波浪力[20]

F(z,t)=FD(z,t)+FI(z,t)

(21)

式中：FD(z,t)和FI(z,t)分别为拖曳力和惯性力，其表达式为

(22a)

(22b)

式中：ρ为海水的密度；D为桩柱的直径；CD和CI分别为拖曳力系数和惯性力系数，文献[21]建议CD=1.2及CI=2.0。

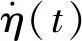
(23)

式中：σu(z)为水质点水平速度u(z,t)的均方差。 对于海浪随机过程η(t)采用P-M谱时，σu(z)可近似写为[22]

(24)

式中：H1/3为三分之一有效波高。

于是，随机波浪力的等价线性表达式为

(25)

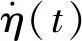
在式(23)中， 对于任意点z=zi处的拖曳力随机过程FD(zi,t)和z=zj处的随机过程FD(zj,t)， 其功率谱密度函数可写为

SDij(ω)=Sη(ω)Gi(ω)Gj(ω),i,j=1,2,…,n

(26)

式中：SDij(ω)为随机过程FD(zi,t)和FD(zj,t)的功率谱密度，Sη(ω)为海浪随机过程η(t)的功率谱密度，Gi(ω)的表达式为

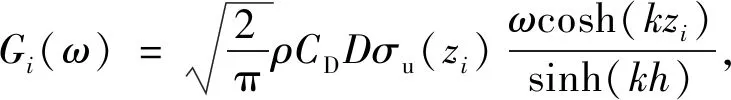
(27)

因此，n维拖曳力平稳随机向量过程FD(t)=[FD(z1,t),FD(z2,t),…,FD(zn,t)]T的功率谱密度矩阵为

(28)

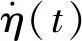
(29)

式中：Li(ω)的表达式为

(30)

最后，n维波浪力平稳随机向量过程F(t)=[F(z1,t),F(z2,t),…,F(zn,t)]T的功率谱密度矩阵可表示为

SF(ω)=Sη(ω)×

(31)

在上述Morison公式中，得到的拖曳力和惯性力的功率谱密度矩阵是一个非负定的Hermitian矩阵，满足本征正交分解的要求。

4 计算实例

为了验证本文方法的有效性，采用文献[23]中直立小圆柱桩进行分析，取桩底为原点，海底平面水平向为x轴，竖直方向为z轴，模拟10个等间距点处的波浪力随机过程，并与Monte Carlo方法的模拟结果进行比较，波浪力沿z轴的分布如图1所示。

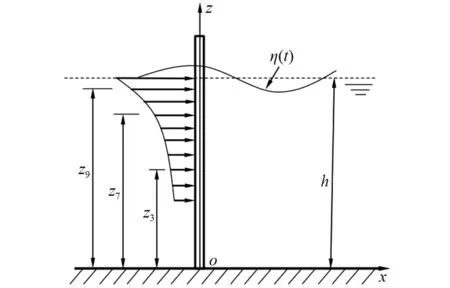
图1 波浪力沿z轴的分布

在此算例中， 波高谱采用P-M谱

(32)

式中：g=9.81 m/s2为重力加速度；v为海面以上19.5 m处的风速，取v=16.24 m/s。

本文算例的具体参数及取值如表1所示。

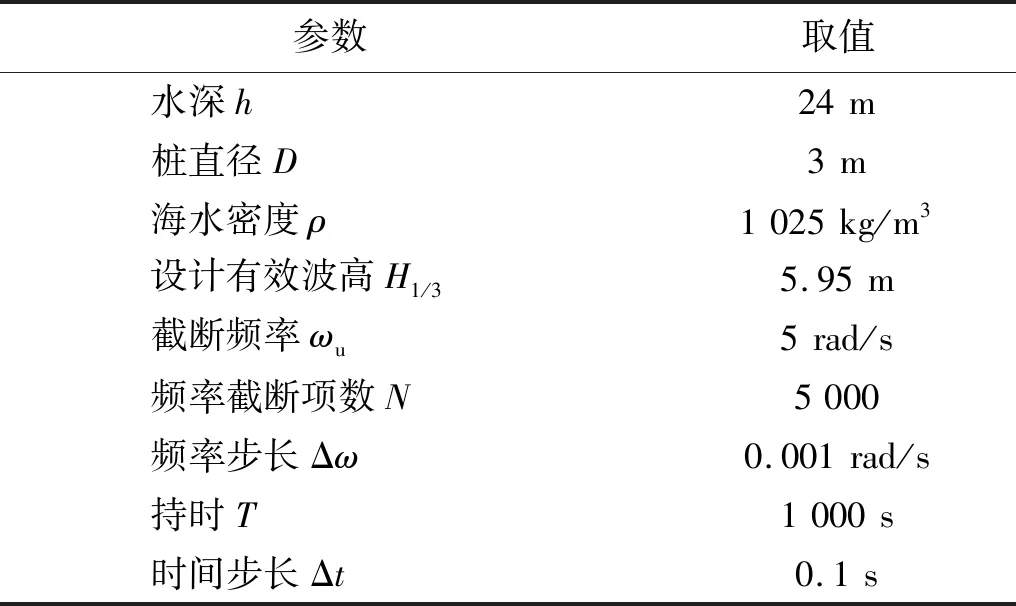
表1 计算参数及取值

图2为本文方法与Monte Carlo法生成位置z3、z7和z9三点处(见图1所示)的波浪力代表性样本曲线(第100条)的比较。由图可知，代表性样本曲线具有平稳随机波浪过程的基本特性，且本文方法与Monte Carlo法生成的曲线在幅值、波长变化等方面具有相似性。

表2为采用本文方法和Monte Carlo方法分别生成10个点处波浪力样本集合的均值及标准差相对误差的平均值，其中，各点处波浪力样本集合的均值相对误差和标准差相对误差的定义见文献[16]。表3为采用本文方法和Monte Carlo方法分别生成10个点处波浪力样本集合所需的总时间。从表2中可知，Monte Carlo方法生成的233条和1 000条样本的均值相对误差均远大于本文方法生成的233条代表性样本均值相对误差；对于标准差相对误差，本文方法生成233条代表性样本的标准差相对误差虽略大于Monte Carlo方法生成1 000条的样本标准差相对误差，但其较小于Monte Carlo方法生成233条样本的标准差相对误差。同时，从表3中可知，Monte Carlo方法生成233条样本的总时间略小于本文方法生成233条代表性样本总时间，但其生成1 000条样本的总时间约为本文方法生成233条代表性样本总时间的3倍。因此，从模拟的精度和效率两方面综合考虑，本文方法生成的233条代表性样本远优于Monte Carlo方法生成的233条样本，也优于Monte Carlo方法生成的1 000条样本。此外，本文方法仅需两个基本随机变量即可精细地表达波浪力随机场，生成的代表性样本数量少，且构成一个完备的概率集，因而与概率密度演化理论具有一致性，这为结合概率密度演化理论进行复杂工程结构的非线性随机动力响应分析和可靠度评价提供了基础。

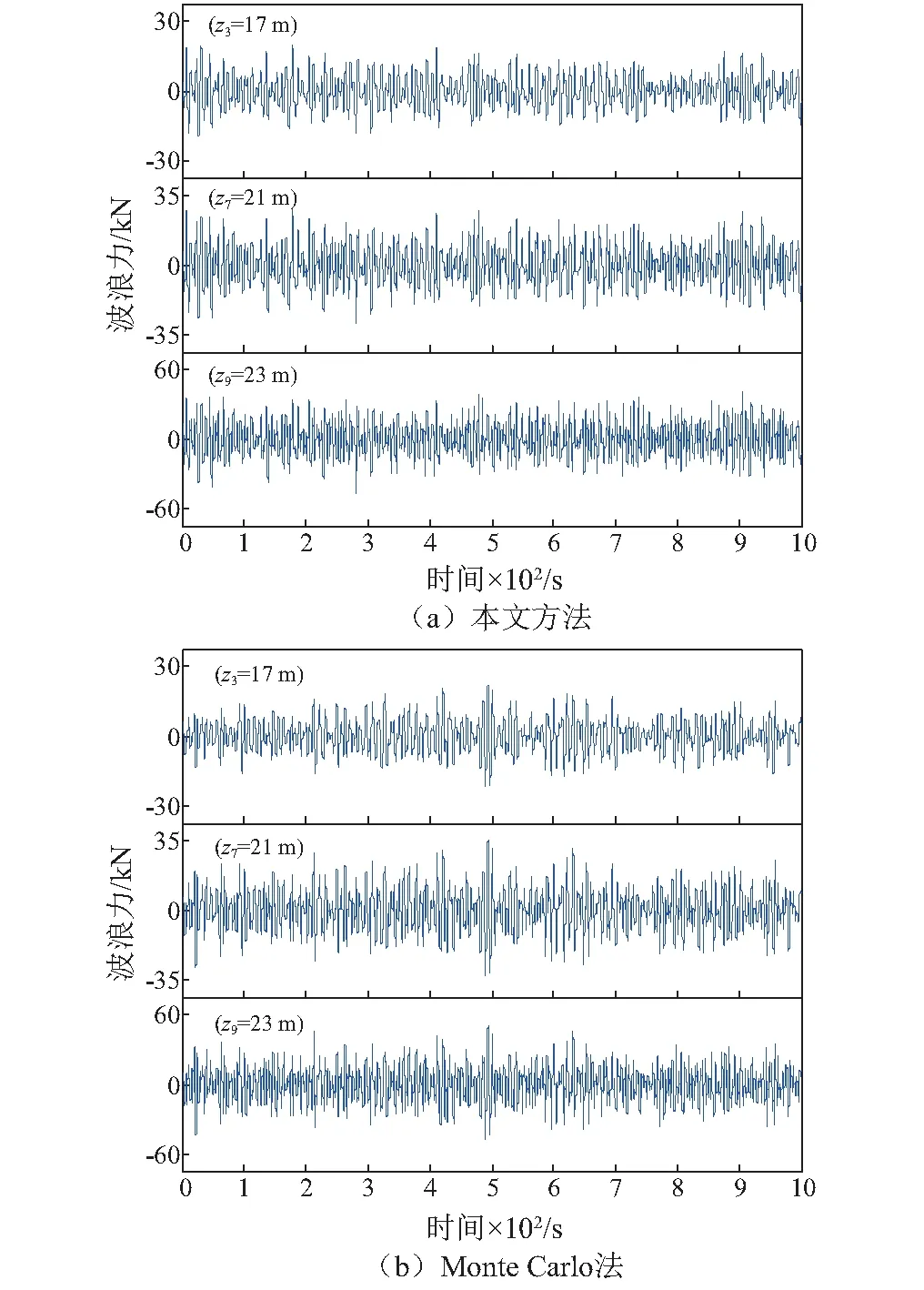
图2 随机波浪力代表性样本

图3和图4分别给出了本文方法在z3和z7两点处生成的233条波浪力代表性样本的自相关函数、互相关函数与目标值比较。为了清晰地反映模拟值与目标值的拟合程度，图3和图4均仅给出了时间区间(-50 s～50 s)的比较结果，同时对自相关函数和互相关函数进行了归一化处理。从图3和图4中可知，点z3和z7处模拟的自相关函数、互相关函数与目标值均拟合一致，进一步表明了本文方法的有效性。

表2 均值和标准差的相对误差

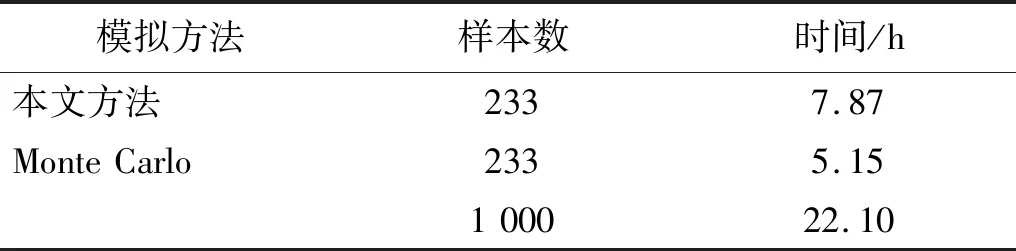
表3 模拟效率比较

图3 自相关函数比较

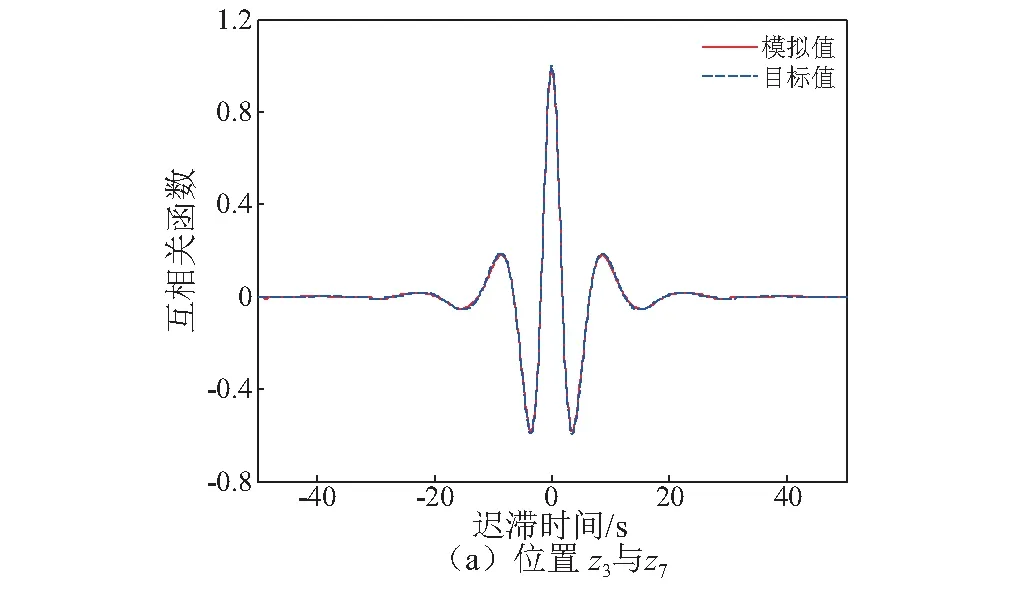
图4 互相关函数的比较

5 结 论

利用波高谱，结合线性化的Morison方程，建立了波浪力随机场的功率谱密度函数矩阵。在基于正交随机变量的本征正交分解上，引入正交随机变量的随机函数形式，实现了波浪力随机场模拟的降维表达。数值算例表明，本文方法具有如下特点：

(1) 结合波高谱与Morison方程，构造了波浪力多变量随机过程。与直接积分法计算整个桩柱上的波浪力相比，本文方法可精细化模拟作用在小尺度桩上每一点处的波浪力随机过程，更符合实际情况。

(2) 基于本征正交分解的降维模拟方法，能够极大地降低波浪力多变量随机过程模拟的随机度(随机变量的数量)。在本文方法中，仅需2个基本随机变量即可模拟波浪力多变量随机过程，从而可利用数论方法选取基本随机变量的代表性点集，实现仅用数百条代表性样本即可在概率密度层次上描述波浪力多变量随机过程的概率特性。

(3) 与Monte Carlo方法相比，本文方法所需的基本随机变量最少，生成的代表性样本数量少，且每条代表性样本具有给定的赋得概率，所有的代表性样本构成一个完备概率集，从而可结合概率密度演化理论进行复杂海洋工程结构随机波浪力作用的非线性动力反应分析。