Preferential orientation of tracer spheroids in turbulent channel flow
2019-07-08YuchengJieLihoZhoChunxioXuHelgeAndersson
Yucheng Jie, Liho Zho,,*, Chunxio Xu, Helge I. Andersson
a AML, Department of Engineering Mechanics, Tsinghua University, China
b Department of Energy and Process Engineering, Norwegian University of Science and Technology, Norway
Keywords:Direct numerical simulation Turbulent channel flow Particle-laden flow Non-spherical particle
A B S T R A C TAxis-symmetric spheroids, such as rod-like and disk-like particles, have been found to orient preferentially in near-wall turbulence by both experiment and numerical simulation. In current work we examined the orientation of inertialess spheroids in a turbulent channel flow at medium friction Reynolds number given based on the half of channel height. Both elongated prolate spheroid and flat oblate spheroid are considered and further compared with the reference case of spherical particle. The statistical results show that in near wall region the prolate spheroids tend to align in the streamwise direction while the oblate spheroids prefer to orient in the wallnormal direction, which are consistent with earlier observation in low Reynolds number() wall turbulence. Around the channel center we found that the orientation of spheroids is not fully isotropic, even though the fluid vorticity are almost isotropic. The mechanism that gives rise to such particle orientations in wall-turbulence has been found to be related to fluid Lagrangian stretching and compression (Zhao and Andersson 2016). Therefore, we computed the left Cauchy-Green strain tensor along Lagrangian trajectories of tracer spheroids in current flow field and analyzed the fluid Lagrangian stretching and compression. The results indicated that, similar to the earlier observations, the directions of the Lagrangian stretching and compression in near-wall region are in the streamwise and wall-normal directions, respectively.Furthermore, cross over the channel the prolate spheroids aligned with the direction of Lagrangian stretching but oblate spheroids oriented with the direction of Lagrangian compression. The weak anisotropy of orientations of fluid Lagrangian stretching and compression observed at the channel center could be the reason for the aforementioned modest anisotropic orientation of spheroids in channel central region.
Particle-laden flows are in a great variety of engineering processes [1] and natural phenomenon [2]. In practice, the flow is normally turbulence and the dispersed particles are often with irregular shapes, which is more complicated and of fundamental interest.
The non-spherical particles are usually modelled as axissymmetric spheroids, i.e. prolate (rod-like) spheroid and oblate(disk-like) spheroid. Intensive studies by experiments and numerical simulations on the dynamics of inertialess spheroidal particles in homogeneous and isotropic turbulence (HIT) have been carried out in past years [3-9]. These studies have shown particles to preferentially align with respect to fluid vorticity,which causes particle rotation to differ from that of fluid element, even though the particles are massless. Specifically, rodlike particles tend to align their symmetry axis with the local fluid vorticity vector, which leads them to rotate preferentially around their symmetry axis [5]. Disk-like particles align one of their longest axes with the local fluid vorticity, leading to the rotation normal to their symmetry axis. In other words, “rods spin and disks tumble” [9]. Furthermore, Ni et al. [8] showed that the fluid vorticity and long rods independently aligned with the Lagrangian fluid stretching direction in isotropic turbulence.
There were also extensive studies on the dynamics of spheroids in wall turbulence. Challabotla et al. [10] and Zhao et al. [11]investigated the inertialess spheroids in the turbulent channel flow and observed that the orientation of prolate and oblate spheroids are preferentially aligned in streamwise and wall-normal direction, respectively, in the near wall region. Such kind of preferential orientation distribution has been further explained by the analysis of Lagrangian fluid stretching and compression along the trajectories of the inertialess particles [12]. The influence of particle orientation on the rotational dynamics of particle is of importance and the behavior of inertialess spheroid in Couette-Poiseuille flow indicates that the anisotropy of particle orientation plays a dominating role on particle rotation mode [13].
In present work, we examined the orientation of inertialess spheroids in channel flow at a medium Reynolds number and the focus of the study is to understand the weak anisotropy of particle orientation in channel center.
In this work, an Eulerian-Lagrangian approach is adopted to study the orientational dynamics of spheroidal particles without inertia. Each individual particle is tracked along its trajectory in the turbulent flow field obtained by means of direct numerical simulations (DNSs) at frictional Reynolds number.The frictional Reynolds number is defined based on the wallfriction velocityand the channel half-height. The DNS data of flow field is obtained from the Johns Hopkins Turbulence Database.
A point-particle approach is used for tracking the spheroids with elongated and flat shapes. The governing equations of the rotation of massless spheroids were given by Ref. [14] as:

Here the Eq. (1) is formulated in the particle frame-of-reference with origirticle center of mass and coordinate axes aligned with the principal directions of inertia.The particle rotation vector are determined by both fluid rotation vector and the fluid strain rate tensor . The shape of particle is characterized by eccentricity defined as, whetio as and 2c is the length of the symmetry axis and 2a(2b) is the length of one of the two other axes. Therefore,represents the prolate spheroid, is for oblate spheroid while is for spheres.
Initially 100000 particles with eccentricityare randomly distributed in the fully developed turbulent field, see Fig. 1. The statistics given in the following section are obtained by averaging in the homogeneous directions, i.e. the streanwise and spanwise directions, and in time.
The orientation of spheroid normally can be represented by the mean absolute direction cosines of the angle between particle symmetry axis and the principle axes of inertial frame.As shown in Fig. 2, the orientation of spheroid is heavily shapedependent. We observed that the elongated prolate spheroid tends to align in the streamwise direction while the flat oblate spheroid preferentially orients to the wall-normal direction. The spheres, as we expected, orient randomly in the flow field regardless of their location. Those findings are in consistency of earlier studies in low-Reynolds-number channel flow [10].
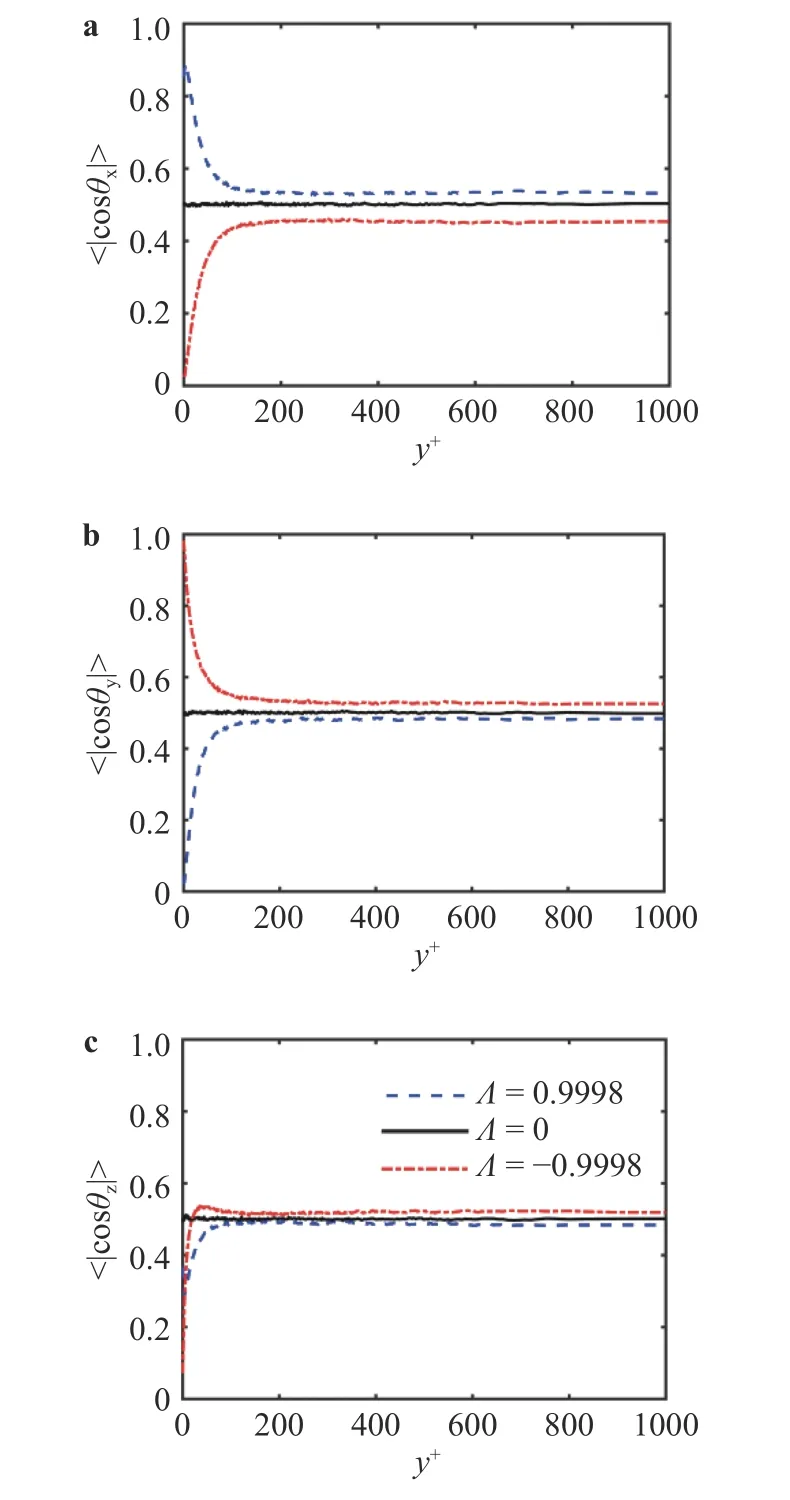
Fig. 2. Mean absolute direction cosines of oblate (= -0.9998),spheres (=0) and prolate (=0.9998) spheroids relative to a the streamwise direction, b the wall-normal direction, and c the spanwise direction
In the region of channel center, where the vorticity field is almost isotropic, however, we found the very modest anisotropy of particle orientation (see Fig. 2). In order to reach a better understanding of this observation, we further examined the orientation of fluid Lagrangian stretching and compression relative to the three axes of inertial frame as shown in Fig. 3. Ni et al. [8]and Zhao et al. [12] have pointed out that the orientation of prolate and oblate spheroid with no inertia is mainly induced by the fluid Lagrangian stretching and compression, respectively. This finding seems universal in both HIT and wall turbulence. Figure 3 shows that close to the wall the fluid Lagrangian stretching/compression is aligned in the streamwise/ wall-normal direction, which is similar to the behavior of spheroids.However, in the channel center both Lagrangian stretching and compression are anisotropically oriented in a modest manner,which, in our view, explains the observed weak anisotropy of spheroids orientation in the central region of the channel. The details of computation of Lagrangian fluid stretching and compression can be referred to the work by Ni et al. [8].
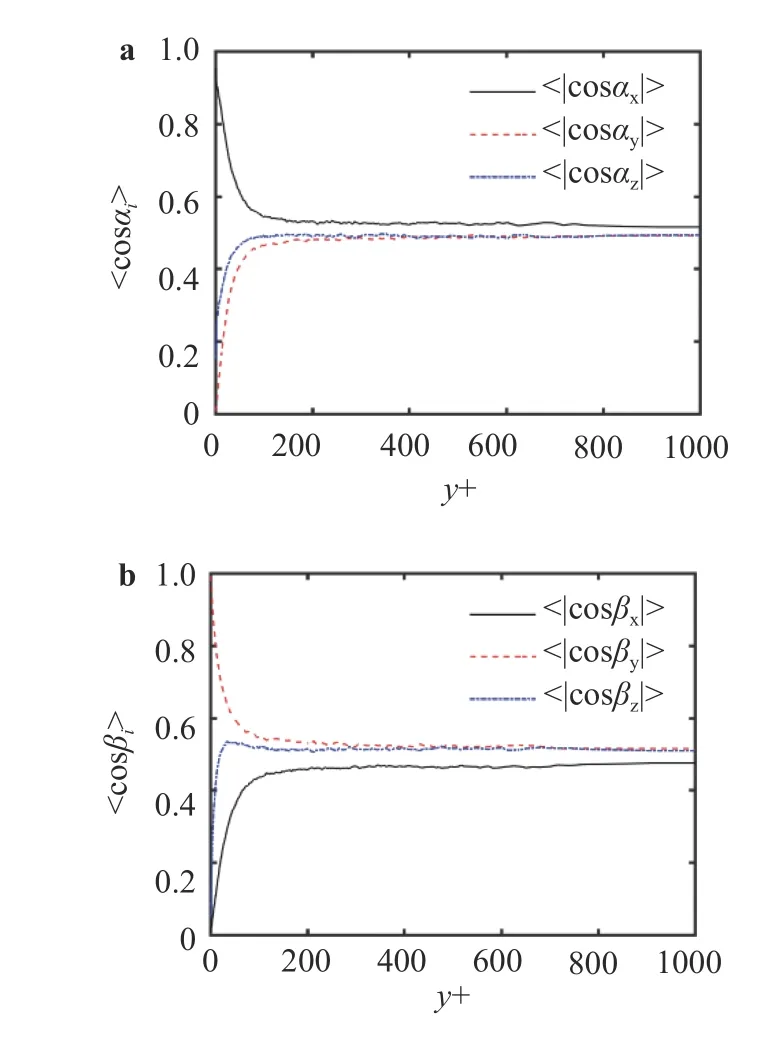
Fig. 3. Orientation distribution of Lagrangian fluid a stretching and b compression relative to the axes of inertial frame
The present study is focused on the orientation of inertialess spheroids in a turbulent channel flow at medium friction Reynolds number. We considered both prolate and oblate spheroids with a reference case of spheres. The statistics show a modest anisotropy of particle orientation in the channel center region. To better interpret this observation, we performed the analysis of Lagrangian fluid stretching and compression and found that the weak anisotropic particle orientation is mainly caused by the similar orientational behavior of Lagrangian fluid stretching and compression.
Acknowledgments
We gratefully acknowledge the financial support from the National Natural Science Foundation of China (91752205,11702158 and 11490551). Computing time was granted by the Programme for Supercomputing (NN2649K).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Mechanics of Tokamak fusion components
- Delamination strength of HTS tape under transverse tensile stress and its enhancement by using different Ag layer depositing temperatures
- Numerical study of MHD mixed convection under volumetric heat source in vertical square duct with wall effects
- Progress on design and related R&D activities for the water-cooled breeder blanket for CFETR
- Numerical methods for the magneto-mechanical coupling analysis of invessel components in Tokamak devices
- Progress on the ultrasonic testing and laser thermography techniques for NDT of tokamak plasma-facing components
