无线传感网络的标量信源估计的研究

周 胜，石艳红

(南京科技职业学院信息工程学院， 南京 210048)

目前，无线传感网络(Wireless Sensor Networks,WSNs)[1-2]广泛应用于环境检测、数据收集领域，如森林防火检测、康复医疗。在这些应用中，部署了多类的传感节点。通过这些传感节点收集数据。然而，传感节点所在的区域环境是复杂多变的。在某一个区域可能同时存在多个信号源(信源)，因此，导致传感节点所收集的信息较大。同时，由于通信环境的多变，节点所采集的信息包含了噪声。

因此，如何从包含噪声的信息中，分离或提取所需的源信号是提高WSNs应用的关键。换而言之，就是从观察的噪声信息中估计信源。目前，研究人员对信源估计进行了大量的研究。例如，文献[3]利用协作WSNs分析了标量信源参数的分布式估计问题，分析表明：依据信源的统计信息和噪声，多类估计算法具有低的均方误差(Mean Square Error,MSE)。类似地，文献[4-6]也分别基于可获取的信源知识，分析了最大似然估计(Maximum Likelihood Estimator,MLE)[4]、最佳线性无偏差估计(Best Linear Unbiased Estimator,BLUE)[5]和最小均方误差(Minimum Mean Square Error,MMSE)估计的性能。

然而，现存信源估计算法是基于高斯噪声场景，并没有考虑脉冲噪声。在实际环境上，环境内观测的信号多数包含脉冲噪声[6]。例如，在变电区域中，由多个电设备所产生的噪声均为脉冲特性[7]。目前，研究人员只分析了脉冲噪声的影响[8]。但是，这些研究并没有考虑脉冲噪声对估计算法性能的影响。

文献[9]分析了利用MMSE的最优贝叶斯估计(Optimal Bayesian Estimation,OBE)对受Middleton Class-A噪声影响的高斯信源的估计性能，其分析表明：提出的MMSE-OBE的性能依赖于接收信号的统计特性。此外，文献[10]也推导了MMSE-OBE。然而，文献[9-10]的分析局限于点-点场景，并且没有考虑信道衰落的影响。查询现有文献，目前没有文献针对基于瑞利衰落的脉冲噪声环境下，估计高斯信源以及研究估计算法的性能。

为此，本文基于瑞利衰落信道环境，分析了脉冲噪声对信源估计的影响。并考虑Middleton Class-A脉冲噪声的存在，对信源进行估计，并提出最优贝叶斯估计(Optimal Bayesian Estimator,OBE)。OBE算法针对瑞利衰落信道，推导了高斯信源的估计的表达式，并分析了OBE的最小均方误差(Minimum Mean Square Error,MMSE)的性能。仿真数据表明，提出的OBE算法的性能优于LMMSE估计算法。

1 系统模型

令s表示信源，其均值为高斯分布。信源s受Middleton Class-A噪声n影响，则所观察的信号y可表示为：

y=s+n

(1)

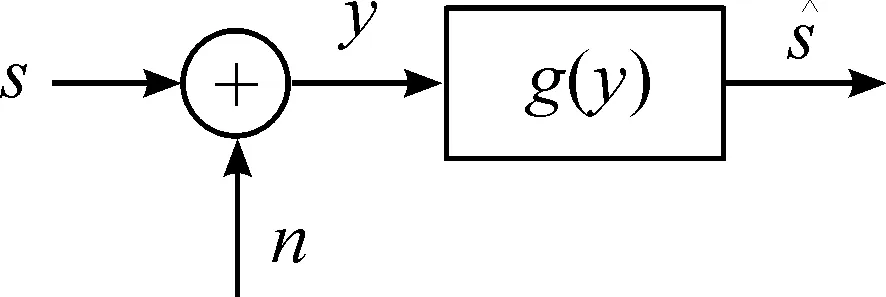
图1 信源估计模型

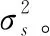
假定xi表示第i个传感节点所测量的信号，表示如下：

xi=his+ni,i=1,2,…，M

(2)

式(2)中，hi，ni分别表示信道参数、第i个传感节点处的噪声。

ϑ

(3)

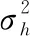
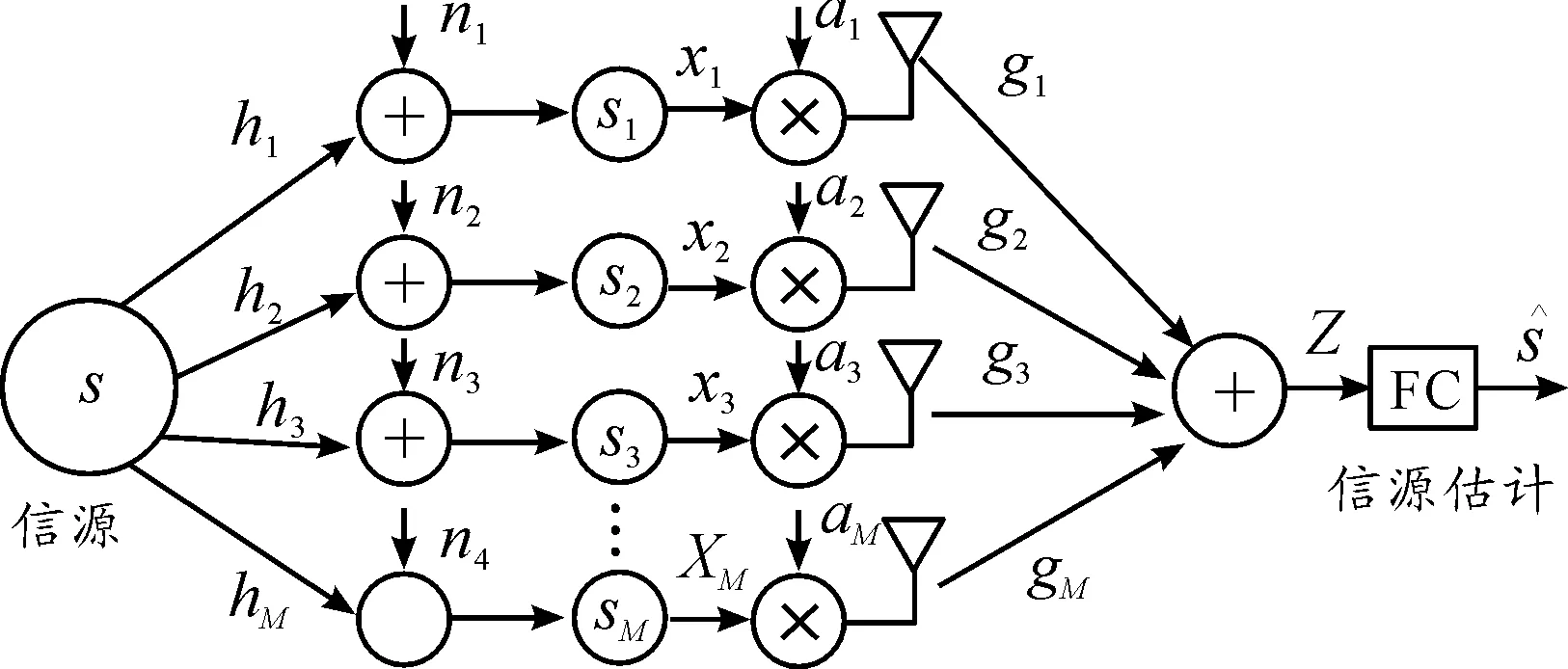
图2 面向分布式WSNs的高斯信源估计模型

假定ϑ服从Middleton Class-A分布，其表征脉冲通信干扰。因此，ϑ的概率密度函数(Probability Density Function,PDF)表示如下[7]：

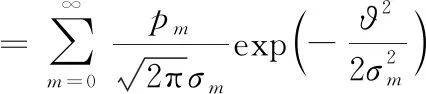
(4)

2 最优贝叶斯估计

利用最优贝叶斯估计算法对噪声信源进行估计，表示如下：

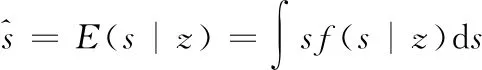
(5)

首先，对式(3)重新编排，可得：

z=gTWhs+gTWn+ϑ=αs+β

(6)

式(6)中，g=[g1,…，gM]T；h=[h1,…，hM]T；W=diag(α)，其中α=[α1,…，αM]T。且n=[n1,…，nM]T。每个节点的放大因子αi的定义如下：

(7)

式(7)中，PT表示所有传感节点的总的传输功率，且α=gTWh、β=gTWn+ϑ。

假定N=gTWn与ϑ为相互独立分布，β的分布可表示为：

(8)

(9)

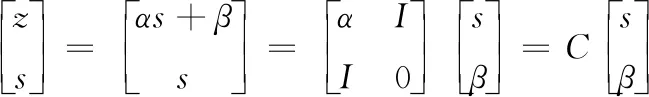
(10)

依据联合的高斯混合分布[10]，可得：

(11)

式(11)中Cμm为:

(12)

而C∑mCT的定义如下：

(13)

从式(11)的联合分布可知，条件PDFf(s|z):

(14)

式(14)中χm(z)的定义如下:

(15)

再利用文献[13]中的理论 10.3，可得：

(16)

(17)

最终，依据式(5)和式(13)可得，在给定z条件下s的MMSE-OBE估计值：

(18)

当ni和ϑ均为高斯变量时，相应地，s的MMSE估计如下：

(19)

3 OBE算法的MSE性能

本文第2节推导了对标量高斯信源的MMSE-OBE估计值。本节分析OBE的均方误差MSE性能。即选用MSE作为性能指标，表示如下：

(20)

式(20)中，∑s|z表示后验方差。其定义如下[10]：

(21)

然后，依据式(20)可得：

(22)

(23)

然后，采用LMMSE估计推导MSE上限MSEUB，表示如下：

MSEUB=MSELMMSE=

(24)

4 数值分析

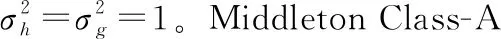
建立两个实验。第一个实验分析OBE算法的性能，即分析式(18)的输入-输出关系；第二个实验分析OBE算法的MSE性能。

4.1 实验一

图3显示了式(18)的输入-输出关系。从图3可知，A值的增加，使得脉冲噪声更逼近于高斯噪声，最终使OBE算法的输入-输出特性曲线与高斯噪声AWGN的曲线相近。换而言之，A值的降低，使得环境更具有脉冲性，导致输入-输出的非线性更突出。这就类似于点到点场景(脉冲噪声的存在引起测量值z的非线性)。因此，在这种场景下，OBE估计算法表现为非线性。从这些数据说明，在设计分布式估计算法时，应充分考虑脉冲噪声特性。

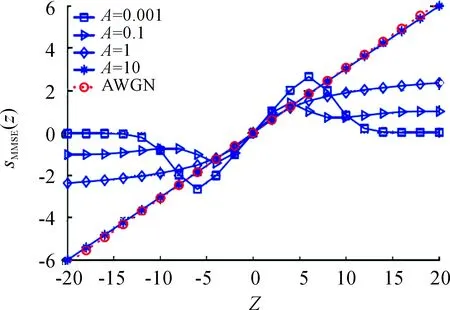
图3 OBE算法的输入-输出特性

4.2 实验二

本次实验分析OBE算法的MSE性能。测量SNR和通信SNR均为0 dB。传感节点数从0～500变化。实验数据如图4所示。图4中的LMMSE表示MSE的上限MSEUB。从图4可知，OBE算法的MSE性能类似于高斯场景。MSE性能随传感节点数的增加呈指数下降。并且随传感节点数增加，提出的非线性MMSE估计收敛于LMMSE估计，即逼近于上限MSEUB。同时，也观察到，在传感节点数增加的情况下，OBE算法的MSE性能并没有随A的影响。

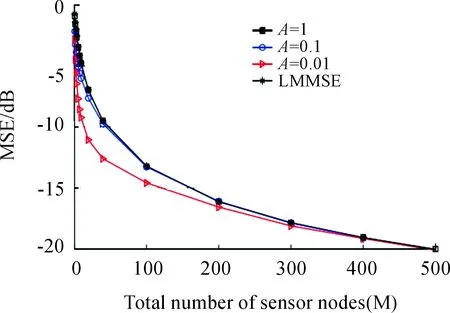
图4 OBE算法的MSE性能

5 结论

无线传感网络由空间分布的传感节点组成，其系统参数是未知，需要通过有效技术估计未知参数。本文考虑了WSNs中Middleton Class-A噪声存在，并分析了标量高斯信源的分布式估计，推导了MMSE的最优贝叶斯估计的闭型表达式，并分析了MSE上限和下限。数据分析表明，推导的OBE算法的性能优于LMMSE估计。