侧倾底凹结构对火炮弹丸阻力的影响

陆海波,高 洁

(1.南京炮兵学院 炮兵军事理论创新与作战实验中心， 南京 211132；2.江阴职业技术学院外语系， 江苏 江阴 214433)

自火炮诞生伊始，提高火炮的射程就是火炮设计人员和使用者的不懈追求。对于主要起火力压制作用的中大口径火炮而言，更远的射程无疑会使本方在非接触性作战中取得更大的优势。目前提高炮弹射程的弹药增程方法主要有底凹减阻、底排减阻[1-2]、助推火箭发动机、冲压发动机[3-4]、滑翔增程[5]以及各种方法组合使用的复合增程[6]等。

采用底凹减阻技术的火炮弹丸称之为底凹弹，具体是指底部带有凹腔的旋转稳定式炮弹[7]，由美国在20世纪初最先开始研制，可用于杀伤爆破弹、子母弹和特种弹等[8]。在各种弹药增程技术中，底凹弹丸具有结构简单，不引入其他介质，在运输、贮存等过程中要求少，容易保障等优点，从而使得底凹弹的研究受到重视。谷嘉锦[9]以风洞实验研究手段，验证了底凹结构对弹丸的减阻作用，且在底凹结构上带有导气孔的底凹弹丸具有更小的气动阻力。Fournier等[10]为了深入了解底凹弹底部复杂的流动结构，采用计算手段研究了高超声速(马赫数范围3.5-5.75)的锥柱裙弹丸结构，并与自由飞行实验结果进行了比较。王中原等[11]提出了一种底凹弹在超音速条件下侧壁开孔减小底阻的数学力学模型。鞠玉涛等[12]数值模拟了标准与底凹弹形的绕流流场，得到了流场参数分布及底部涡流结构的变化规律。Howell等[13]对作为底阻有效削弱手段的底凹结构展开了研究。结果表明，对于普通凹腔，在较宽的凹腔深度变化范围内，弹体总体阻力减小。他们还进一步研究了通风槽对弹体阻力以及凹腔的影响。王芳，郎田，魏志芳等[14]以某122底凹榴弹为例，研究了不同马赫数和不同底凹深度条件下，底凹弹丸的受力特性。Evrard等[15]从流动机理的角度展开了研究，发现足够深的底凹结构有助于形成并保持尾流的对称性并且底凹减阻的机理在于RSB模态的静态三维涡系与底面的相互作用及其稳定抑制。轩海彬，张文洁，于勇等[16]采用大涡模拟的方法对亚跨声速流动中底凹弹体绕流流场进行了非定常数值模拟，探索其减阻的流动机理。

位于底凹弹尾部的回流流动是底凹结构减阻的关键，本文从增强回流流动“压力恢复”能力的角度出发，在传统的柱状底凹结构底凹弹的基础上，通过数值模拟研究了具有不同“收缩倾角，α”(如图1)的底凹结构对弹丸的飞行阻力的影响，得到了不同收缩角底凹结构弹丸的超声速绕流流场参数分布和气动阻力系数，并对不同底凹结构底凹弹的受力特性进行了分析。为下一代新型底凹弹的设计提供理论支持。

1 数值计算方法

基于火炮弹丸绕流流场的轴对称特性，使用可压缩的轴对称N-S方程为控制方程[17]

(1)

式中，x为流向，r为径向，

τ为剪切应力，q为热通量，ρ，u，v，T，p，e分别为流体的密度，轴向速度，径向速度，温度，压力以及单位质量流体的能量，e=ρ[CvT+(u2+v2)/2]。

湍流模型采用经典的k-ε模型[18]。对流通量使用Van Leer格式处理，黏性扩散项采用2阶中心差分格式，时间项使用LU-SSOR的隐式格式离散分解。

流动边界条件数据如表1所示。计算中认为壁面无滑移并且使用了绝热壁假设。

为了研究带“收缩侧倾”的底凹结构对弹丸的飞行阻力的影响，分别计算了“收缩侧倾角，α”为0°(无收缩)，2°，5°，10°，15°的五组算例。

表1 流动边界条件数据

计算模型网格(以α=15°为例)如图2所示。

图2 计算模型网格(α=15°)

2 数值模拟结果与分析

2.1 流场参数分布

图3～图7分别给出了不同“收缩角”底凹结构底凹弹绕流流场的流线、马赫数云图以及压力分布。由图可见，由于弹丸外部轮廓一致以及超声速流场扰动只能向后传递的特性，各算例绕流流场的差别主要出现在弹丸尾部底凹结构处。沿流场从前至后，在弹丸头部，形成了经典的脱体弓形激波；弹体外形进入圆柱段时出现一个膨胀区；在弹尾，流动沿弹体侧壁与低端形成急剧膨胀。就底凹结构处的流场而言，当“收缩角”较小时(比如α=2°)，尾部回流的情况与没有“收缩角”(α=0°)的相似，在底凹结构内存在一个统一的大的回流区。随着“收缩角”增大，弹丸底端面的厚度增加，在流场纵截面上形成明显的“台阶”，此时，底凹结构内的回流区域在回流的内部被一分为二，并且当弹丸底端面足够厚，在底端面处也会形成明显的回流区域，图8给出了α=10°算例的尾部流动放大。

各算例绕流流场的温度分布相似，如图9所示(以α=10°算例为例)，在底凹结构内部存在高温区域。

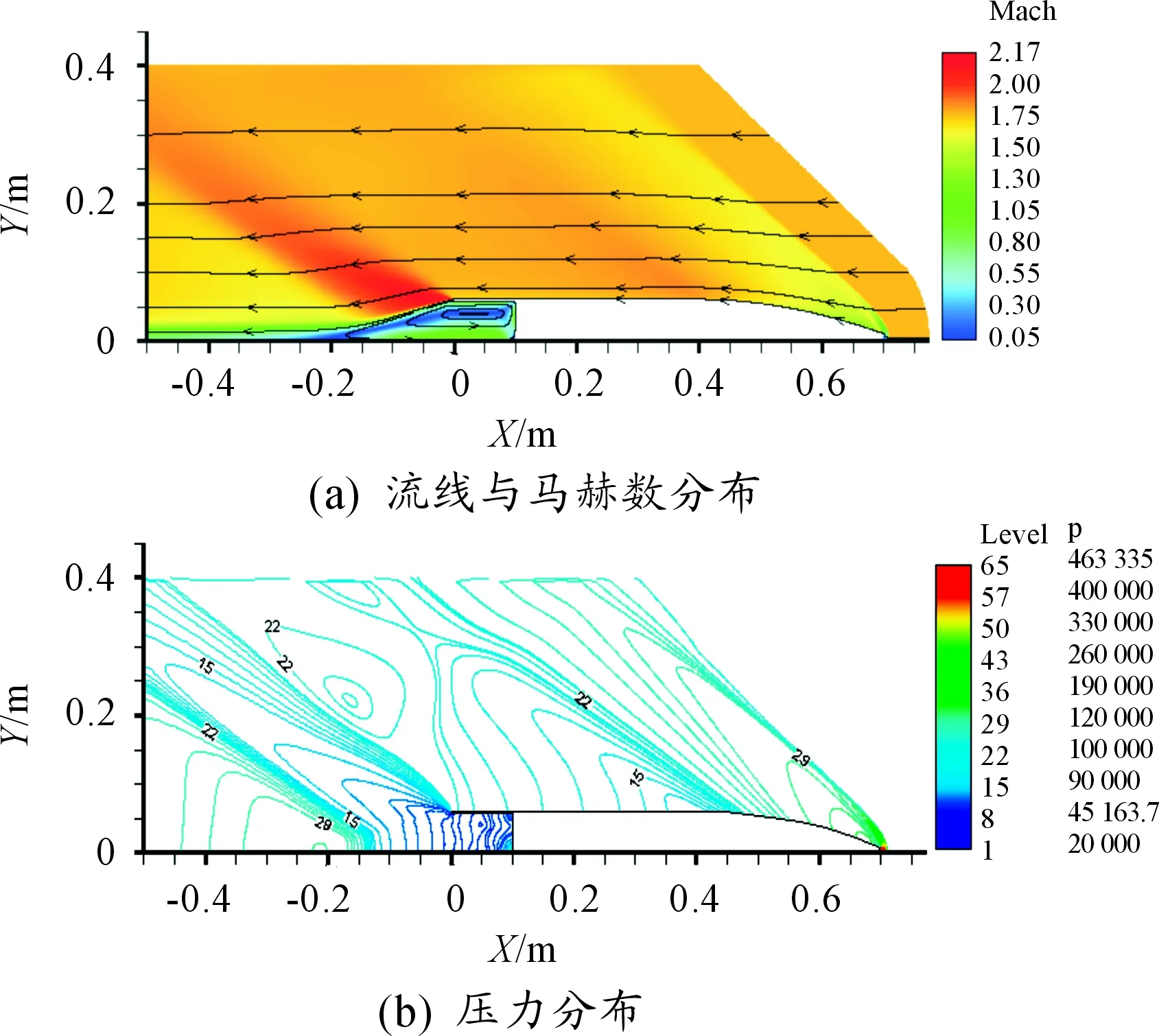
图3 α=0°底凹弹流场参数分布

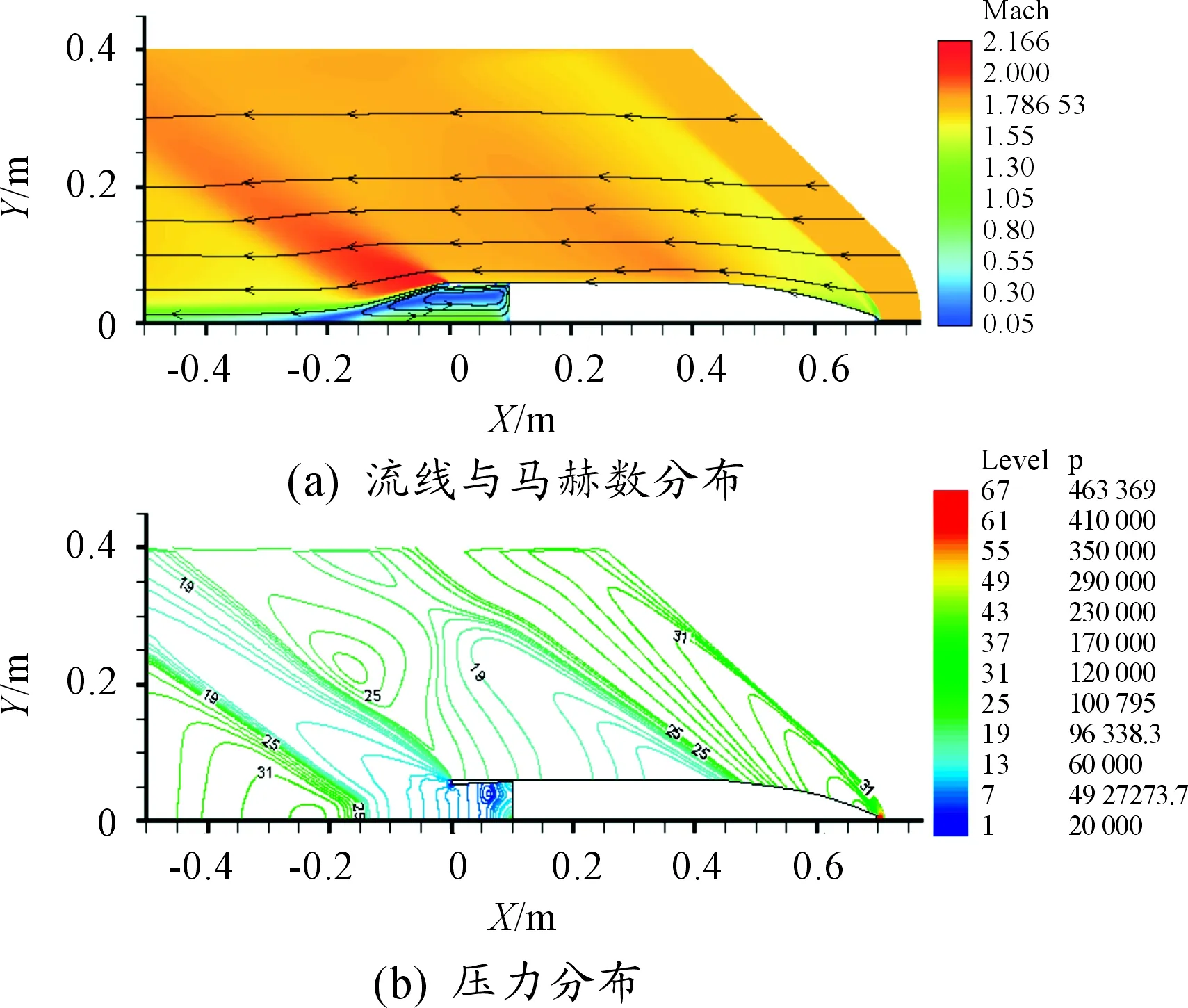
图4 α=2°底凹弹流场参数分布

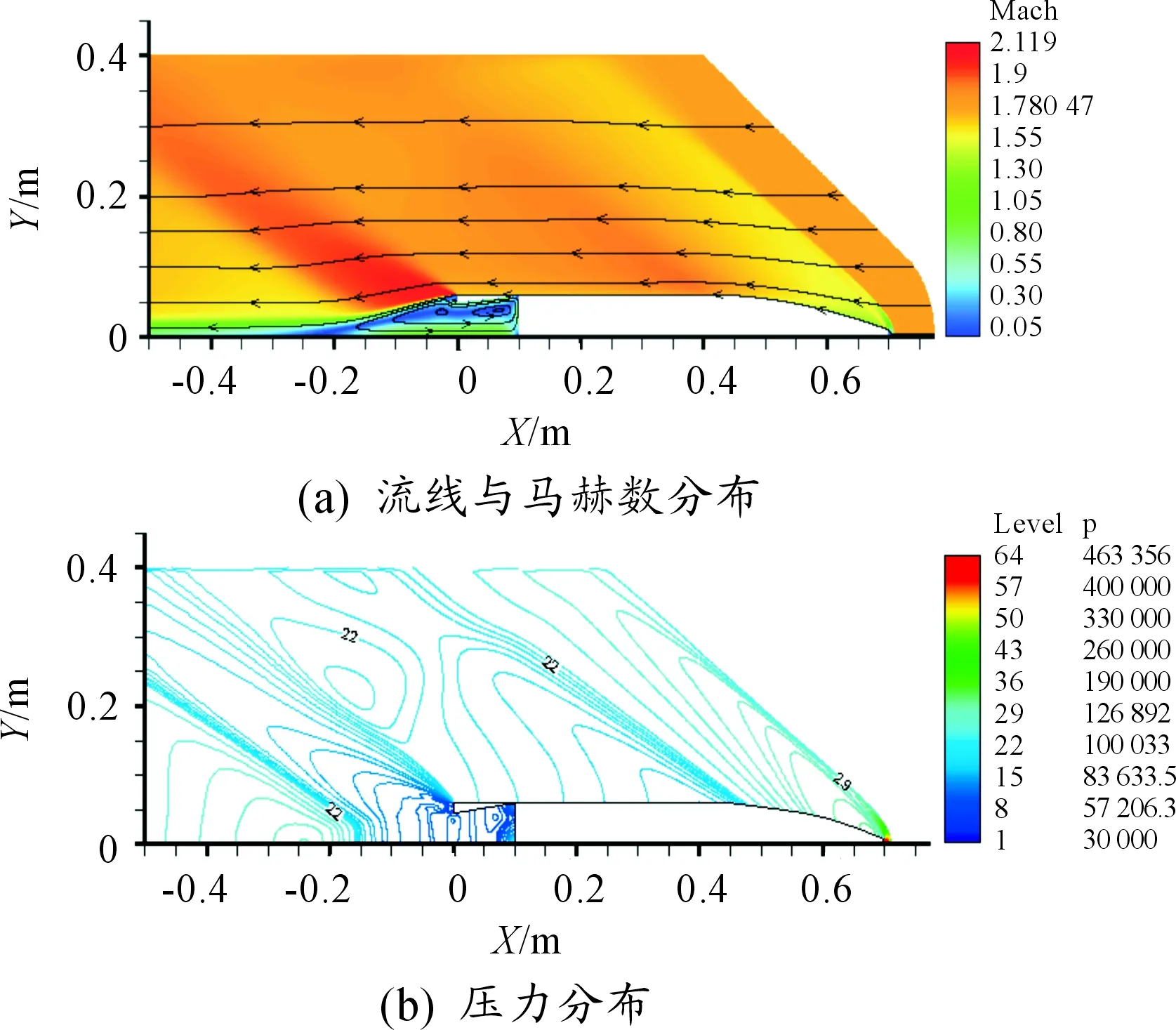
图5 α=5°底凹弹流场参数分布

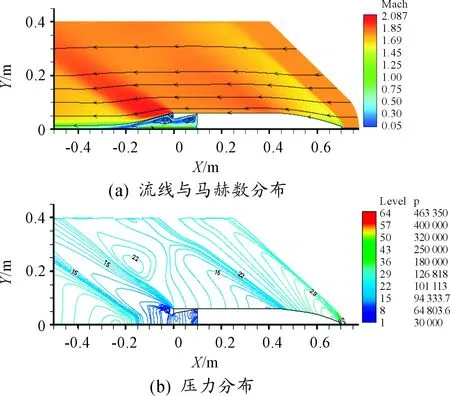
图6 α=10°底凹弹流场参数分布

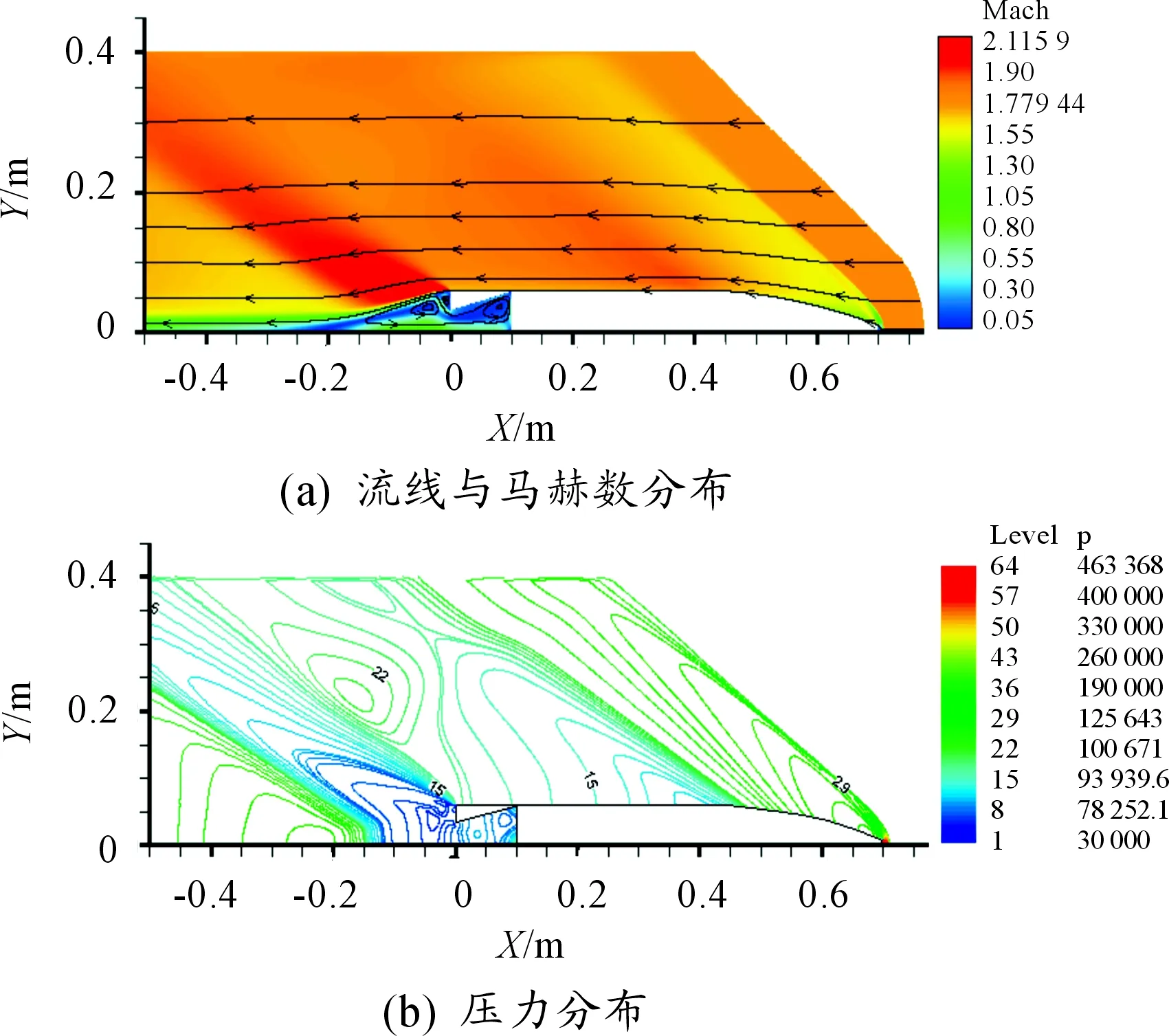
图7 α=15°底凹弹流场参数分布

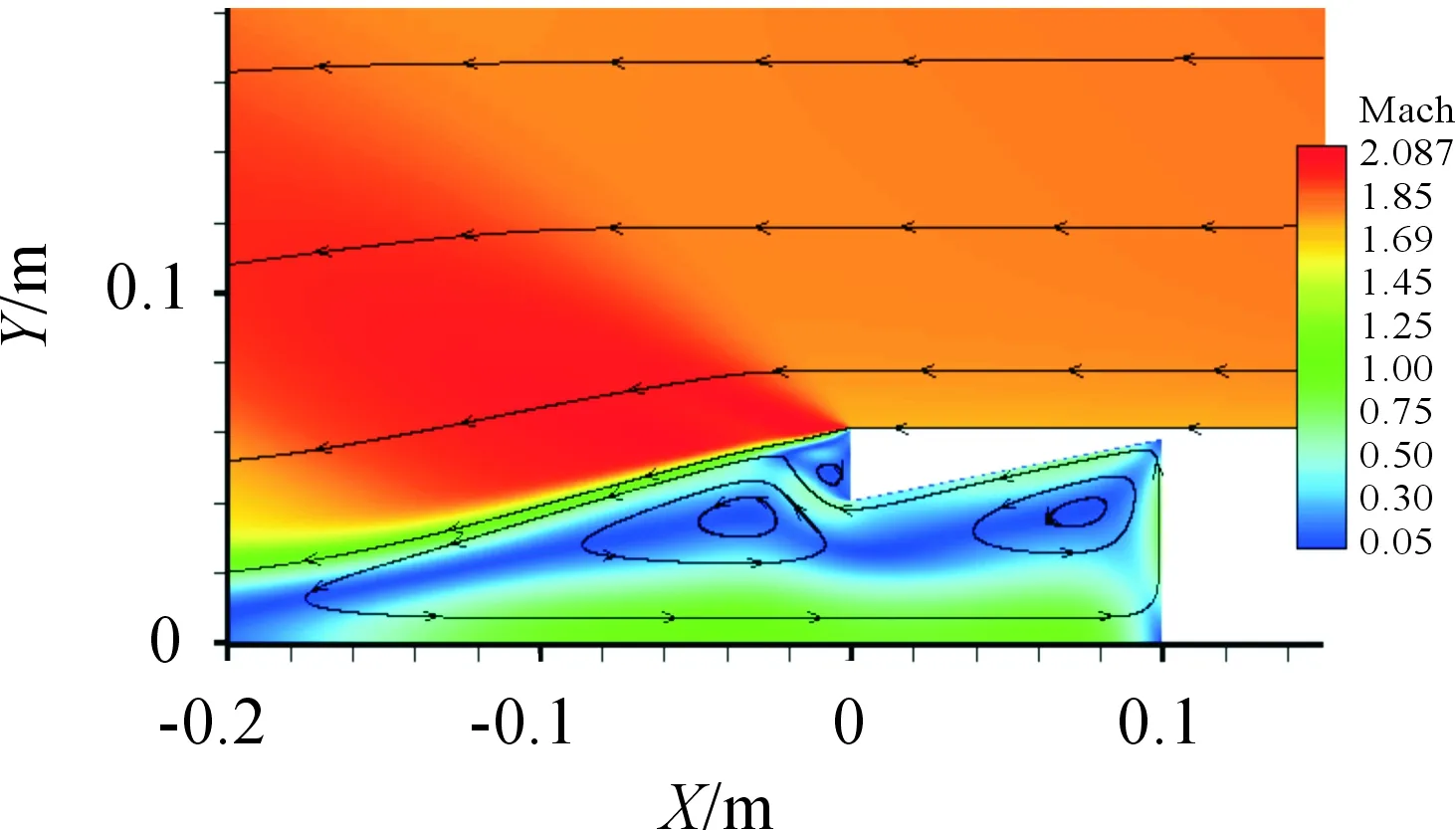
图8 底凹弹底部流动放大(α=10°)

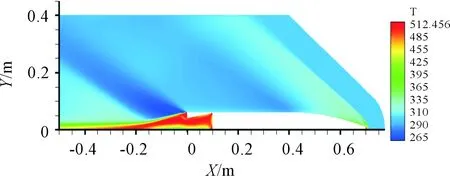
图9 温度分布(α=10°)

2.2 气动阻力

弹丸气动阻力系数(Cd)计算式如下：

(3)

式中，Fd为气动阻力，ρ∞为来流密度，u∞为来流速率，Sref为参考面积(弹丸最大横截面积)。

图10表示各算例的气动阻力系数。由图10可见，收缩结构的引入相比传统柱状的底凹结构(α=0°)，可以有效的减小弹丸的气动阻力。随着底凹结构“收缩角，α”的增大，气动阻力的变化趋势先减小后增大。在本文的计算范围内，α=5°的算例有最小的气动阻力。

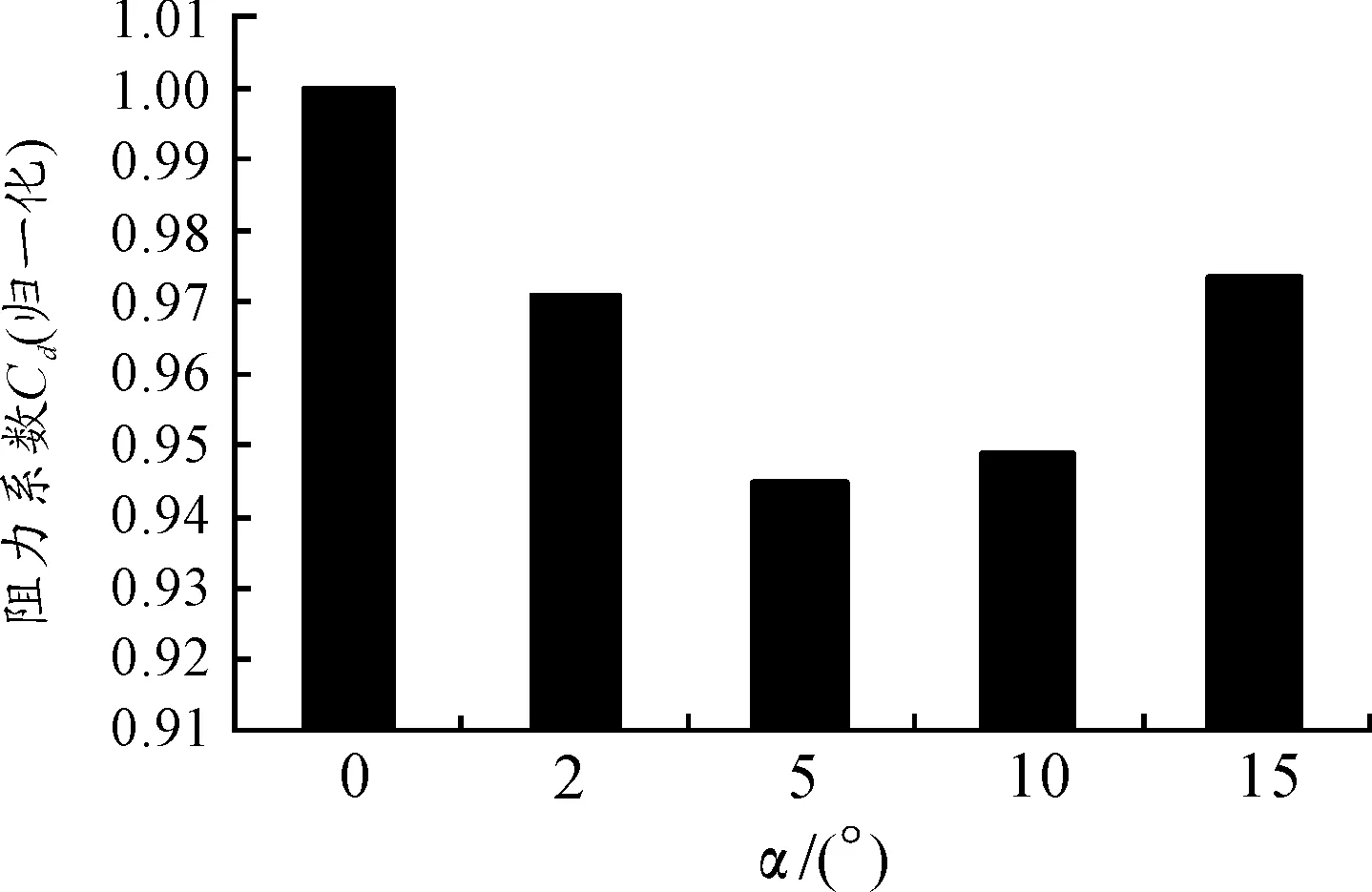
图10 各算例气动阻力系数

图11显示各个算例的底凹结构底面圆(图中A系)、侧壁圆台(图中C系)以及弹丸底面圆环(图中B系)上的压力分布。对于α=0°与α=2°的底凹算例，由于其弹丸底面圆环面积以及底凹侧壁圆台在轴向投影都很小，所以文中不讨论对应表面上的压力分布情况。

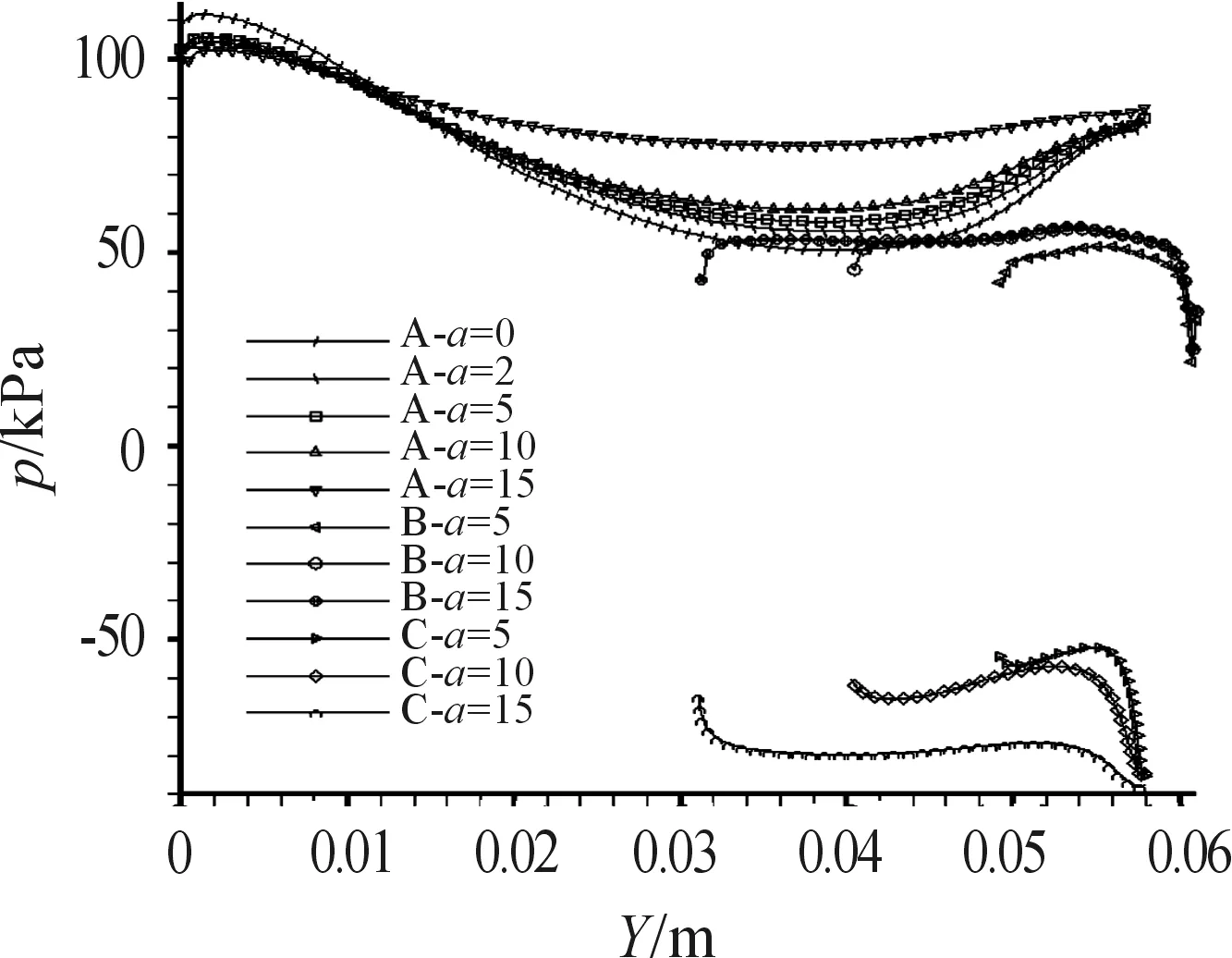
图11 各算例底部压力分布(A：凹腔底面圆；B：弹底圆环；C：凹腔侧壁)

由图11可见，对于弹丸底凹结构底面圆上的压力分布(A系)而言，随着“收缩角”的增大，底凹底面圆上压力分布总体呈提高的趋势。就弹丸底面圆环上的压力分布(B系)而言，底面圆环上压力分布也呈现随着“收缩角”的增大压力提高的趋势。仅就对弹丸减阻起“正面”效果的底凹底面圆以及弹丸底面圆环上的压力分布趋势看，随着“收缩角”的增大，弹丸应当具有更小的阻力系数，然而这与图10给出的实际气动阻力系数计算结果相违背。出现这样情况，原因在于，在底凹结构中，由于“收缩角”的引入，凹腔的侧壁不再与弹体轴向平行，侧壁母线旋成的圆台上的压力，会增大弹丸的底阻。

图11中的“C系”结果即为各算例底凹结构侧壁母线旋成的圆台上的压力分布，由于此压力对弹丸减阻而言起“反”效果，所以取负号。由图可见，随着“收缩角”的增大，侧壁上的压力数值有较大的提升。带有“收缩角”结构的底凹弹气动阻力的分析必须兼顾底凹结构底面圆(A系)、侧壁圆台(C系)以及弹丸底面圆环(B系)三者的压力分布。图10所示的计算结果就是它们共同作用的结果。

除了分析相关表面的压力还要考虑各表面的面积因素。按本文算例模型设置，各算例的底凹底面圆面积一致，但是各底凹结构收缩角的不同，使得其对应的侧壁圆台和弹丸底面圆环的面积也有较大区别，表2给出了底凹结构底面圆、弹丸底面圆环以及侧壁圆台轴向投影的等效面积。由表2可见，随着“收缩角”的增大，弹底圆环与底凹侧壁圆台受压等效圆环的面积也有较快增长。图10所示的计算结果就是它们共同作用的结果。

结合图11与表2，虽然随着“收缩角”的增大，位于底凹结构底面圆和弹丸底面圆环上的压力升高，可以削弱弹丸的气动阻力；但是与此同时，虽然随着“收缩角”的增大，底凹侧壁上的压力也呈现较快上升趋势，且底凹侧壁圆台的等效受压面积也迅速增大，使得弹丸的底阻增大。结合“正、反”两方面的效果，最终，α=5°这样的，“收缩角”大小居中的，底凹结构具有最优的减阻效果，采用该“收缩角”的底凹弹获得了有最小的气动阻力。

表2 各算例底部面积

3 结论

1) 收缩结构的底凹构型相比于传统的圆柱状底凹结构，具有更优的减阻效果。

2) 随底凹“收缩角”的变化，弹丸气动阻力的变化趋势并不单调。在本文计算条件下，“收缩角”α=5°的底凹构型具有最佳的减阻能力。

3) 底凹结构底面圆、侧壁圆台以及弹丸底面圆环上的压力数值都体现为随收缩角增大而增大。但是侧壁圆台之上的压力方向与另两者相反，所以弹丸的最终受力是由三者的大小以及受压面积共同作用的结果。

4) 处于弹丸尾部以及伸入底凹结构内部的回流是底凹减阻的关键因素。当收缩角足够大，会将传统底凹结构内的大的单独的回流区从内部一分为二。

5) 对于底凹结构内部的回流而言，“收缩角”越大，回流的“开口”越小，较小的回流“开口”有助于提高底凹结构内部的压力(包括对减阻起促进作用的凹腔底面压力和起削弱作用的凹腔侧壁压力)。

6) 本文为了减少数值计算结果中的其他因素的影响，单纯的研究底凹结构外形变化对弹丸流场、受力的影响，忽略了在实际弹丸设计中弹带以及船尾等等对底凹弹丸流场的影响，实际的外形设计还需综合考虑弹丸的飞行稳定性、质量、结构强度等因素。