带有双弯曲肋片的细通道流动与传热的数值模拟

钟亿晗，林清宇，冯振飞，李 欢，艾 鑫（广西大学机械工程学院，南宁 530004）

0 引言

诸多工业领域的突破性进展是由微型化技术和先进的冷却技术推动的，在现代高科技中起到重要作用的微芯片是典型的代表[1]。现代高度集成化与精细化的电子元件相较于传统的电子元件存在着受热不均匀、稳定性差、温度极易过高等问题，因此解决电子元件的散热问题成为现代科技发展的重要目标。过去，为了使电子元件的换热过程简单易控，通常在其换热部件中设置用于流体流动的常规尺寸通道，但是时至今日，常规尺寸通道的散热性能已经不能满足现代电子元件的散热需求，而细通道散热器由于在传热方面的高性能和紧凑的结构，在现代集成电子器件的冷却方面显示出优势[2]，在现代工业领域的散热中表现出较好的性能。此外，细通道中的被动式强化传热不需要增加额外的能源，只需通过改变通道的形状、增加肋柱等来增强流体的换热，因此，这种方法受到许多相关研究学者的关注[3]。

在微细直通道的研究中，夏国栋等[3]用数值模拟的方法研究了带内肋凹穴型微通道热沉内部流体层流流动与传热的情况，并且根据热力学第二定律建立了变截面微通道的熵产模型，通过对熵产的分析证实了内肋和凹穴的共同作用使微通道的传热效果明显优于光滑直通道；翟玉玲等[4]用数值模拟的方法分析了间隔扇形凹穴型微通道层流流动与传热的情况，该通道由扇形凹穴型微通道[5]与各个通道之间的间隔段组成，证明了间隔扇形凹穴型微通道在综合传热性能上要优于光滑矩形微通道；两者的研究均证实，改变微通道的形状可以提高微通道的换热性能。Wang等[6]在细直通道上设置了具有一定厚度的均匀分布的双倾斜肋片，并采用数值模拟的方法分析了肋片高度及其数量对微通道传热和流动性能的影响；艾鑫等[7]研究了肋片尺寸的改变对带有双倾斜肋片的细通道传热性能的影响，二者的研究结果均证实：加入双倾斜肋片的细通道可以达到强化传热的效果；冯振飞等[8]采用数值方法研究微柱体对微通道热沉内流体流动、传热和综合性能的影响，证实了微柱通道综合性能优于光滑通道，有错位量的微柱通道更优。

笔者在光滑细直通道模型的基础上添加几组双弯曲肋片，通过数值模拟的方法对带有双弯曲肋片的细通道中的流体流动特性、传热特性以及微通道的综合性能进行了研究。

1 数值模拟

1.1 模型介绍

通道计算模型的宽Ws为4.5 mm，高Hs为2.5 mm，长度L为50 mm，通道宽W为3.5 mm，高H为2.5 mm，相邻通道肋宽的一半d为0.5 mm。通道内设有7对圆弧状弯曲的肋片，其沿着流动方向对称布置（如图1所示）。肋片高度h为1.0 mm，厚t为0.3 mm，圆弧角度α为90°。每对肋片的肋片间隙距离A为0.6 mm，相邻两对肋片间距s为4.5 mm。基于不同的圆弧半径R，可得到三种不同的微通道MCDR-0.2、MCDR-0.4、MCDR-0.6，对应的半径r值分别为0.2 mm、0.4 mm、0.6 mm。为了对比无肋片细通道的传热、流动以及综合性能，同时模拟了光滑矩形细通道（MC）在同条件下的性能。

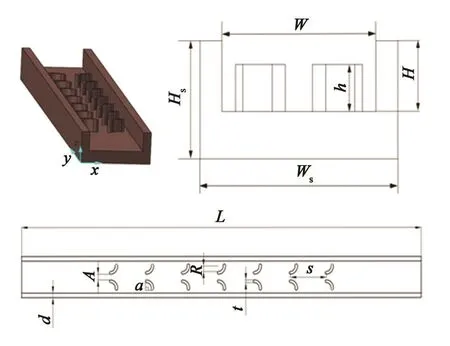
图1 带有双弯曲肋片的细通道几何结构示意图Fig.1 Schematic diagram of mini-channel with doublecurved ribs

1.2 数学模型

模型分为固体域和流体域两个部分，固体域由铜组成，流体域由水组成。由于模型设置的出口段过小导致了液体产生回流的现象，因此增加了出口过渡段，长度为30 mm。假设模型中的水为牛顿流体，且不可压缩；流体的流动处于稳定的层流状态；固体和流体的热力学性质不变，同时忽略黏性耗散重力及辐射传热的影响，流体的具体参数值参考文献[9]。根据以上假设建立流体域控制方程：

连续性方程：

动量方程：

流体域的能量方程：

固体域的运动方程：

式中：U为流体的速度矢量，m/s；p为压力，Pa；Tf为流体温度，K；Ts为固体温度，K；λf为流体热导率，W/（m·K）；λs为固体热导率，W/（m·K）；ρ为流体在对应温度下的平均密度，kg/m3；μ为黏度系数，Pa·s；Cp为定压比热容，J/（kg·K）。

模型的边界按条件设置：通道入口处流体为匀速，流体的入口速度uin分别为0.16 m/s、0.22 m/s、0.28 m/s、0.34 m/s、0.4 m/s，入口处的温度恒为303 K，通道出口处压力设置为pout=0；雷诺数由式（5）求得，范围为376～941；通道底面设置为热流密度q=500 000 W/m2的恒热流加热。流体介质与固体介质交界处设置为固液交界面且无渗透与滑移，两侧边界壁面设置为周期性边界条件，其余面均视为绝热。

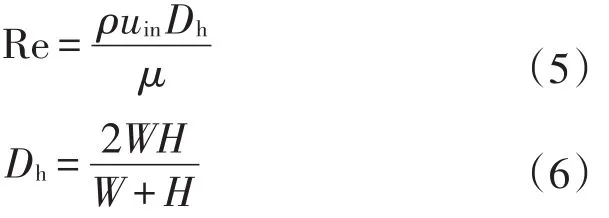
式中：Dh为细通道的水力直径，m；W为细通道入口的宽度，m；H为细通道的高度，m。

1.3 模型求解与网格划分

用CFD软件对上述控制方程求解，收敛残差设为10-5。基于带有双弯曲肋片的细通道模型特点，采用混合网格模式对通道内的流体域及固体域进行划分，对出口过渡段采用非结构网格进行划分。为了确保计算的精度，对网格进行独立性验证。以光滑通道模型（MC）为例，对网格数分别为73×104、170×104、440×104的模型进行对比，以网格数为170×104的模型为基准，流速为0.16 m/s时的进出口压降如表1所列。

网格数较低时产生的相对误差较大，网格数较大时相对误差较低。综合考虑计算时间以及精确度，选用网格数为170×104的模型进行模拟。4组模型基于5种速度得出5种工况，合计20个算例。

表1 模型MC的网格独立性验证结果Tab.1 Results of Molecular IndependenceVerification of Model MC

1.4 数值模型有效性验证

细通道中的平均摩阻系数为

压降为：

式中：pin为细通道入口处的平均静压，Pa；pout为出口处的平均静压，Pa；L为细通道的长度，m;

对于正在发展中的层流，文献[10]提供了计算矩形直通道压降的公式：

其中Po是泊谡叶数，表达式为：

式中：β为入口截面宽高比。

将由式（9）所得的压降与模拟得到的压降进行比较，结果如图2所示。可以看出两者结果十分吻合且趋势一致，最大误差未超过6%，说明研究采用的数值模拟方法是有效可靠的。

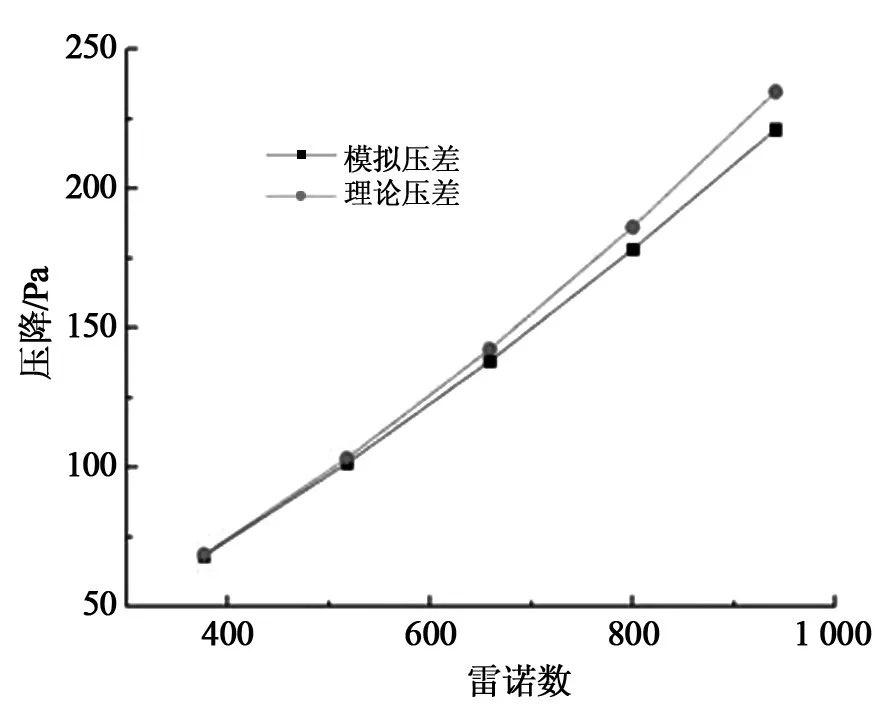
图2 数值计算压降与理论压降的比较曲线Fig.2 Comparison of numerical calculation of pressure drop and theoretical pressure drop

2 数据处理

细通道传热的总热阻计算式为：

式中：Tw，max为热沉底面的最高温度；Tin为细通道入口处的流体温度。

努塞尔数Nu计算式为：

式中：k为传热系数，W/（m2·K），其表达式为：

式中：Aw为固体域的被加热壁面的面积；Asf为流体域与固体域的接触面积；ΔTm为加热壁面温度与流体的进出口平均温度的差值，K，表达式为：

式中：Tout为细通道出口处的流体温度，K；Tw为固体域受热壁面的平均温度，K。

3 结果分析

3.1 流动特性分析

图3为摩阻系数在光滑矩形通道和带有双弯曲肋片的细通道中随着雷诺数变化的情况。在相同的雷诺数下，摩阻系数随着肋片半径R的增大而增大，带有双弯曲肋片的细通道的摩阻系数远大于光滑矩形通道；在同一通道中，摩阻系数随雷诺数增大而减小，且减小的趋势逐渐变小。产生此结果的原因是：流体流入通道遇到双弯曲肋片后，其流动面积会发生突变，即流体在流动过程中遭遇了肋片的阻碍。由于双弯曲肋片本质上还是类似于圆柱体的固体区域，因此流体在遇上双弯曲肋片的时候，尚未形成边界层；而当流体完全接触双弯曲肋片后，会发生边界层分离，并且会在肋片的尾端形成一个尾涡区。尾涡区的漩涡持续消耗流体的机械能，使该区的压力降低而形成压差阻力。

图3 不同肋片半径下摩阻因数随雷诺数的变化曲线

Fig.3 Variation of friction factor with Reynolds number at different rib radius

3.2 传热特性

图4为不同工况下细通道热沉底部的最高温度与雷诺数关系图。由图可知，光滑细通道与带有双弯曲肋片的细通道的热沉底面最高温度有非常大的差距。随着雷诺数的增大，热沉底面的最高温度不断减小；在同一雷诺数下，热沉底面的最高温度随着肋片半径的增加而减小。

图5为带有双弯曲肋片的细通道以及光滑矩形通道在不同雷诺数下热阻RT的变化趋势。可以看出，在雷诺数增大的情况下热阻总体是在减小，减小的速率随着肋片的增大而减缓；在相同雷诺数的情况下，热阻随着肋片尺寸的增大而减小。由图4与图5可以说明，带有双弯曲肋片的细通道的传热性能要优于光滑矩形细通道。进一步分析图5可知，随着肋片尺寸的增加，细通道的传热性能不断增强，尤其是模型MCDR-0.4与MCDR-0.6，其热阻与光滑通道的热阻有很大的差值，由此可以证实，添加双弯曲肋片确实有助于提高细通道的传热性能；热阻数值随肋片半径R增大有靠近的趋势，因此可知，热阻减小的程度随着肋片半径R的增加而减小。

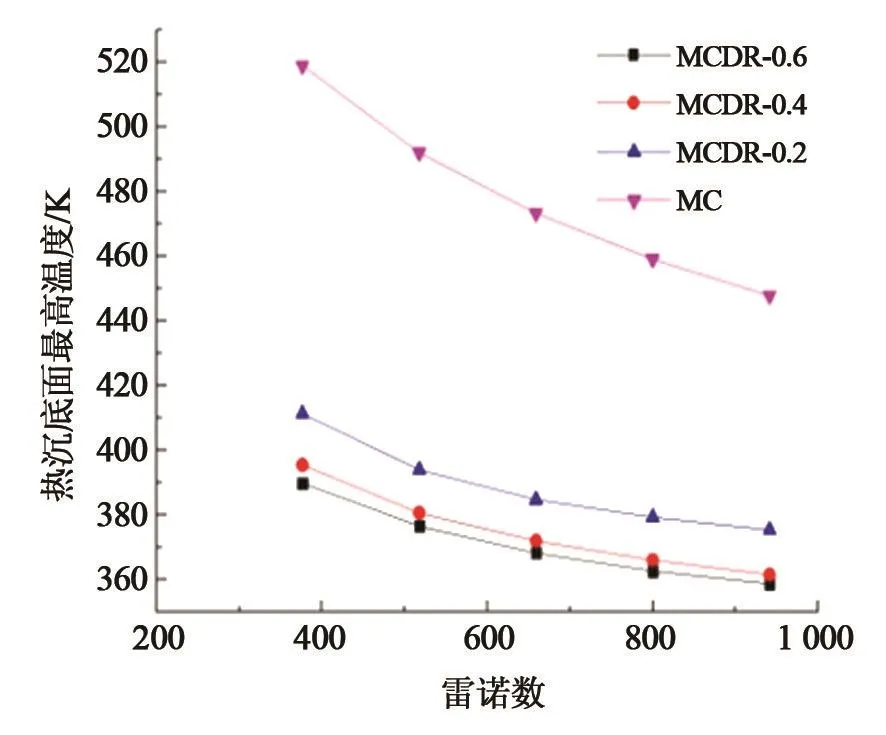
图4 不同工况下的细通道底面最高温度随雷诺数的变化曲线Fig.4 Maximum temperature of the bottom surface of minichannel for different Reynolds number Re under different working conditions

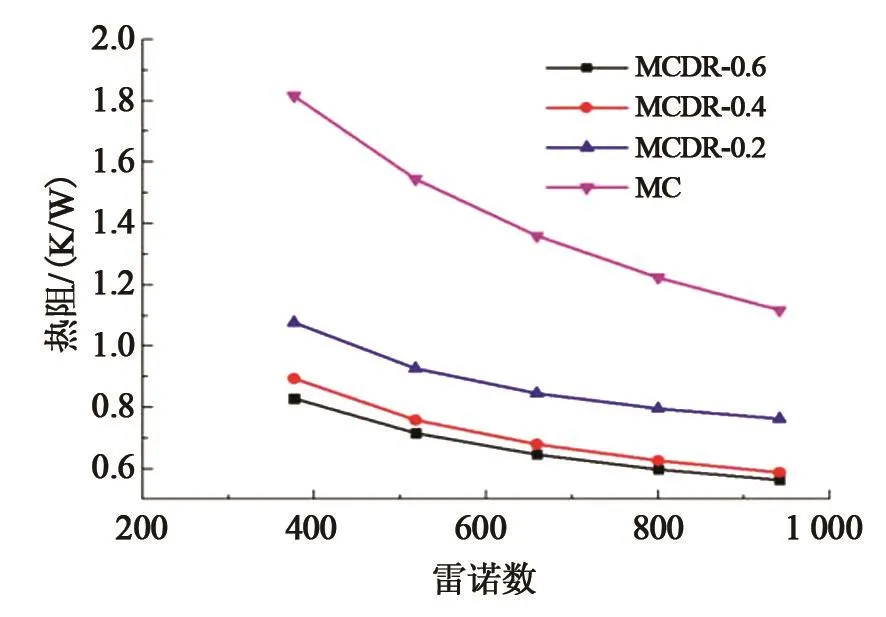
图5 不同肋片半径下热阻随雷诺数的变化曲线Fig.5 Thermal resistance changes with Reynolds number at different rib radius

图6为细通道添加了不同半径的肋片后对努塞尔数的影响。在相同的雷诺数情况下，努塞尔数随着肋片半径R的增大而增大；而MCDR-0.2、MCDR-0.4、，MCDR-0.6的努塞尔数远大于光滑矩形通道的努塞尔数，可知添加双弯曲肋片对于提高通道的传热特性有着显著帮助。这是由于添加了肋片使得流体在流入通道后受到肋片的扰动而使得冷热流体的混合程度增加。在肋片半径最大为0.6 mm时，由于细通道的宽度W非常小，肋片两侧的区域非常小，以至于二次流的扰动程度加强，使得流体更好的混合以达到强化传热的效果。而在肋片半径为0.2 mm时，流体不会选择两肋片中间阻力较大的狭小区域通过，而会选择流过肋片靠外壁面两侧空隙较大的区域，即阻力较小的区域，但依然会有一部分流体从通道的中间流过，此时增强了一部分流体的混合效果，也达到整体强化传热的效果。

图6 不同肋片半径下努塞尔数随雷诺数的变化曲线Fig.6 Variation of Nusselt number with Reynolds number at different rib radius

3.3 综合性能分析

综上可知，双弯曲肋片的添加可以起到强化传热的效果，但同时也增大了流阻。为了客观评价添加肋片对于细通道整体性能的影响，引入综合评价因子[11]PEC（Performance Evaluation Criteria），其定义式为：

式中：Nu和f分别为细通道的努塞尔数与摩阻系数；下标0为光滑矩形细通道（MC）。

图7为不同肋片半径下PEC值随雷诺数的变化趋势。由图可知，带有双弯曲肋片的细通道的PEC值要明显大于光滑细通道的PEC值（即大于1），表明添加双弯曲肋片可以提升细通道的综合性能。在雷诺数较低的时候，带有双弯曲肋片的细通道的PEC值远大于光滑矩形通道的值，表明在雷诺数较低的时候添加双弯曲肋片有较好的综合性能。在带有肋片的细通道中PEC值随着雷诺数增大而逐渐减小，其中MCDR-0.4的减小趋势要小于MCDR-0.6与MCDR-0.2。在同一雷诺数的情况下,PEC值由大到小排序为 MCDR-0.4、MCDR-0.6、MCDR-0.2。由此可知，MCDR-0.4的综合性能优于MCDR-0.2与MCDR-0.6。

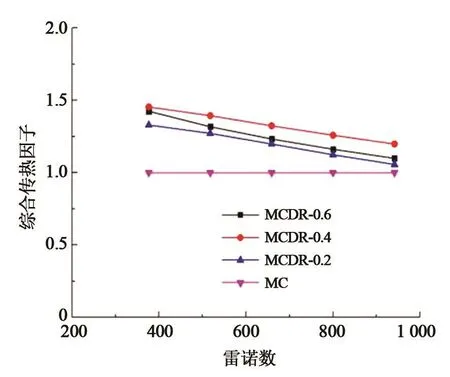
图7 不同肋片半径下PEC值随雷诺数的变化曲线Fig.7 Variation of PEC value with Reynoldsnumber at different rib radius

4 结论

本文设计了一种带有双弯曲肋片的细通道，通过数值模拟的方法研究了MCDR-0.6、MCDR-0.4、MCDR-0.2中流体的流动特性、传热特性以及综合性能，并将结果与光滑矩形细通道的进行比较，得出以下结论：

（1）带有双弯曲肋片的细通道的摩阻系数均大于光滑通道的摩阻系数，说明添加双弯曲肋片确实会提高细通道的阻力；细通道的摩阻系数随着肋片半径的增大而增大，在本研究中，半径R到达最大值0.6时摩阻系数最大；

（2）光滑细通道的热阻远大于带有双弯曲肋片通道的热阻，且光滑细通道的热沉底部最高温度也远大于带有双弯曲肋片通道的热沉底部最高温度，说明添加双弯曲肋片确实可以降低细通道的热阻，强化其传热特性；随着肋片半径的增大，细通道的热阻减小，热沉底面最高温度也减小，表明肋片的半径增大对于降低热阻和强化其传热特性有较强效果；

（3）添加了双弯曲肋片的细通道的PEC值均大于1，说明双弯曲肋片的添加可以有效地提升细通道的综合性能。在雷诺数范围为376～941时，MCDR-0.4的综合性能最好。