冷原子量子真空计量技术研究进展

李 毅，李得天，王多书

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

关键字：冷原子；磁光阱；超高/极高真空；碰撞截面；真空计量

0 引言

超高/极高真空测量技术在宇航科学、纳米科学、半导体制造、表面科学、核聚变、引力波探测等领域具有广泛的应用。目前，测量超高/极高真空度主要采用电离规，其测量下限为1×10-9Pa[1-4]。随着仪器微型化和便携化的发展，尤其是在航天等一些极端环境的特殊应用中，电离规体积和质量较大，很难满足应用需求。此外，电离规需要定期校准，在应用过程中通常还会因自身放气而影响测量准确性。

与传统真空测量技术相比，基于光学方法的真空测量技术具有非接触测量及对真空环境影响小等优点。目前，该技术仅用于特种气体（CO）的测量[5-11]，用于常见真空室本底气体（H2、N2、CO2）和过程气体（Ar、He）测量的报道较少。另外，由于超高/极高真空环境中本底气体稀少，利用吸收光谱技术很难对其进行准确测量。

近年来随着激光冷却和囚禁原子技术的发展，利用冷原子的损失率测量真空度的技术有望发展成为新一代真空计量技术。该技术的压力测量范围在10-4～10-10Pa，甚至可以更低。

本文简述了激光冷却和囚禁原子的基本概念，介绍了磁光阱的结构和工作原理；论述了冷原子量子真空计量技术的国内外研究现状、技术优势和关键技术；展望了冷原子量子真空计量技术的发展趋势。

1 概念与原理

1.1 冷原子量子真空计量技术概念

冷原子量子真空计量技术是在高真空中利用原子的多普勒冷却、磁光囚禁等手段将有限个原子进行捕获，并利用真空中的本底气体对囚禁原子的碰撞作用，使得不同时刻被囚禁的原子数目变化依赖于本底气体的成分及其粒子数密度，通过荧光探测系统测得囚禁原子的数目变化，推算出本底气体的粒子数密度，得到气体压力。

1.2 激光冷却与囚禁原子

1985年朱棣文用6束激光照射钠蒸气室，产生“光学黏团”的原子状态，即冷原子团[12]。目前，能获得冷原子的材料包括碱金属、碱土金属、惰性气体以及放射性同位素等（如Li、Na、K、Rb、Cs、Mg、Ga、Sr、He、Ne、Ar、Kr、Xe、Cr、Ag、Fr等）[13]。制备冷原子团的过程包括：（1）制备原子蒸气；（2）激光冷却原子；（3）将冷原子囚禁到磁光阱、偶极力阱或磁阱中。

1.2.1 原子蒸气制备

在高真空条件下，通过加热将原子蒸发到真空腔中，获得原子蒸气。在高真空下，Li原子只需加热到400℃左右就形成蒸气，Cs原子在室温下可自然形成蒸气。

1.2.2 激光冷却原子

光子具有能量和动量，分别为：

式中：ν为频率；λ为波长；h为普朗克常数。原子的能级是量子化的，只吸收频率大于或等于原子共振频率的光子。图1描述了一个理想、静止、能级为E0和E1的两态原子[14]，波长λ0与式（3）～（4）有关：

式中：c为光速。

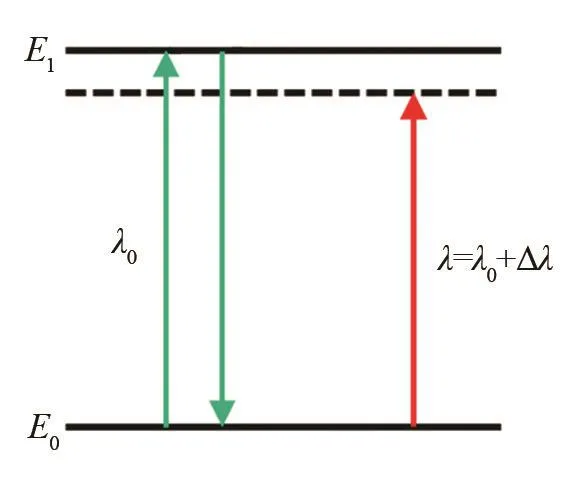
图1 两态原子能级示意图Fig.1 Schematic diagram of energy levels in a two-state atom

处于基态的原子被放置到满足上述条件的光束中，E0能级电子吸收光子被激发到E1能级，之后激发态原子将回到基态辐射光子，由于辐射的光子在各个方向概率相同，因此，原子在激光传播方向受到一个反向冲量，从而减小原子的动量。利用这种原理可以减小原子的速度，实现原子冷却。假设原子的速度为动量为吸收动量为ћk的光子后原子动量发生改变，速度变化为，若原子速度与k方向相同，原子速度变大；若与k方向相反，原子速度减小，如图2所示[15]。通常情况下，利用多普勒效应可选择性改变原子的速度，多普勒频移公式为：

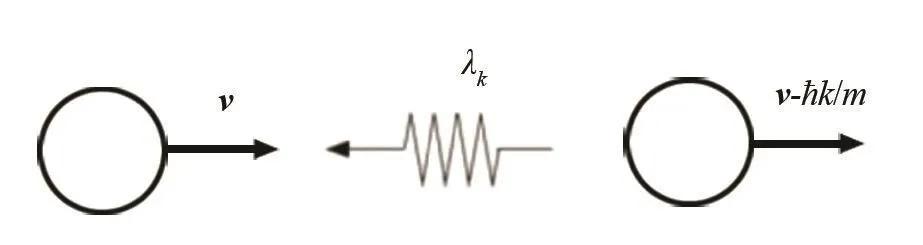
图2 激光囚禁中光与原子相互作用示意图Fig.2 Light interactions of trapped atoms in the laser trapping

如图3所示[15]，利用红失谐激光，只有速度与光子方向相反的原子吸收光子而被减速。与光子运动方向一致的原子不受影响。利用三束相互垂直的激光，从各个方向照射原子，使原子陷于光子持续作用中，运动不断受到阻碍而减速，最后形成“光学黏团”[16]。

1.2.3 磁光阱

由于原子的扩散运动或重力影响，冷原子会很快从俘获区域扩散出来。为了实现空间持续约束，在激光冷却基础上，加入非均匀的磁场，产生依赖于空间位置并总是指向中心的回复力，即磁光阱。

图3“光学黏团”的形成示意图Fig.3 Preparation diagram of optical molasses

磁光阱是一种囚禁中性原子的有效手段，由三对两两相互垂直、具有特定偏振组态并且负失谐的对射激光束形成的三维空间驻波场和反亥姆赫兹线圈产生的梯度磁场构成。磁场的零点与光场的中心重合，负失谐的激光对原子产生阻尼力，梯度磁场与激光的偏振相结合产生了对原子的束缚力，这样就在空间对中性原子构成了一个带阻尼作用的简谐势阱。

为了解释磁光阱的工作原理[13]，假定原子基态总角动量J=0，只有一个能级，在磁场中没有塞曼位移和分裂。激发态J=1，含有三个磁子能级，分别为mJ=0、mJ=-1和mJ=+1。在磁场中，激发态产生塞曼分裂，三个子能级的塞曼位移不同，跃迁频率随磁场强度变化。设磁场是不均匀磁场，在坐标原点处磁场为零，沿z轴两边磁场强度呈线性增大，但方向相反。磁场强度为：

图4[14]是磁光阱原理图，上半部分是原子能级在z轴位置的函数，磁场梯度在z=0处B=0；下半部分是力与位置之间的关系图。图4所示沿z轴的原子能级塞曼位移变化：基态能级和激发态mJ=0子能级不变；激发态mJ=-1子能级沿z轴正向线性降低，沿负向线性增高；mJ=+1子能级相反；能级位移遵从塞曼能量的公式：

式中：gJ为朗德因子；μB为玻尔磁子；mJ为磁量子数。

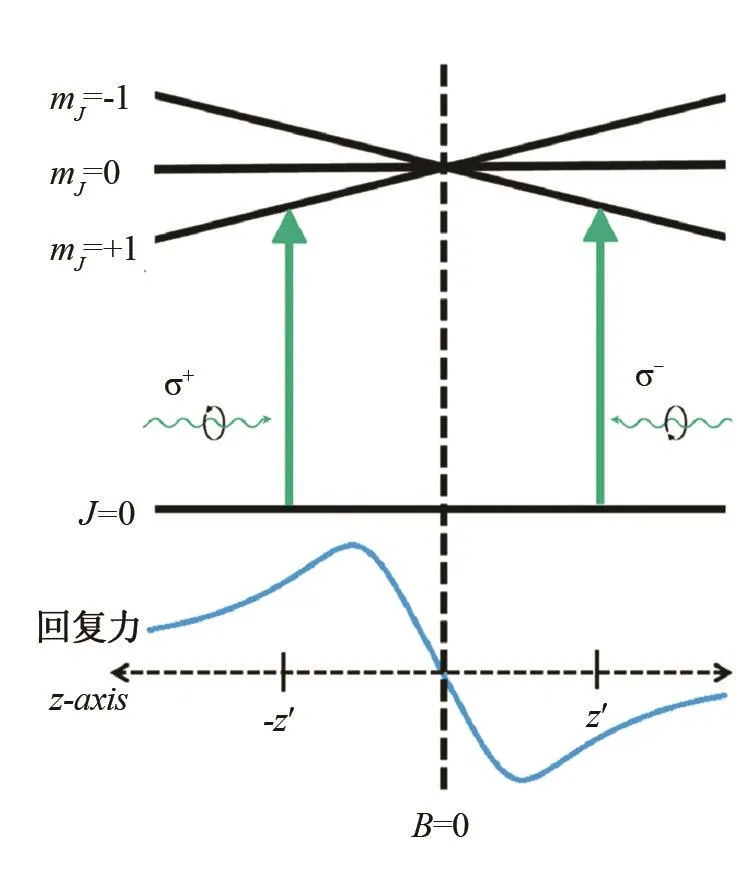
图4 磁光阱原理图Fig.4 Principles of the magneto optical trap

一对强度相等、偏振方向相反的圆偏振光σ+和σ-沿着z轴方向对射，σ+沿z轴正方向，σ-沿z轴负方向，调谐激光频率对z=0处的原子是负失谐状态。由于原子对两束激光的有效失谐不等，处于z＞0位置上的原子将更多地吸收σ-光子，激发到mJ=-1能级，因为激光频率更接近ΔmJ=-1跃迁（失谐更小），从而受到趋于中心的负向力作用；而处于z＜0位置上的原子将更多地吸收σ+光子，激发到mJ=+1能级，同时受到趋于中心的正向力作用。于是所有原子将受到指向原点的辐射压力。越接近原点失谐越大，越接近原点力越小。对于x、y方向，也可得到相似的作用，这样就实现了原子的三维激光囚禁，图5是典型的磁光阱（MOT）示意图[15]。关闭磁光阱中的激光，就是磁阱，陷在阱中的原子具有磁矩，处于中心时势能最低。偏离中心时就会受到不均匀磁场的作用力而返回。

图5 磁光阱结构示意图Fig.5 Schematic of the magneto optical trap

1.3 冷原子量子真空计量技术原理

冷原子囚禁动力学过程可以用装载率公式表示：

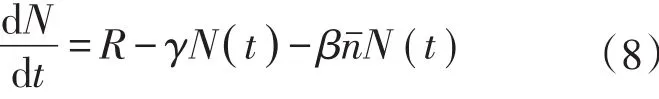
式中：N为被囚禁的冷原子数；R为原子装载率；γ为本底气体与冷原子碰撞而导致的冷原子损失率；βnˉ为冷原子之间的相互作用导致的冷原子损失率，依

为了解上述公式，必须知道nˉ随N的变化，通常考虑N的两种情况[17-18]：N比较小时（小于105个），对于一个固定囚禁体积V，nˉ与N成正比关系：nˉ≈N(t)/V；N比较大时，nˉ是一个常数，V正比N。在囚禁原子密度nˉ是一个常数情况下，上述冷原子囚禁动力学公式可以化简为指数形式：

式中：Γ=γ+βnˉ。此时在囚禁体积不变的情况下，通过测量的装载曲线，用式（9）拟合该曲线，可确定出R和Г。一般βnˉ可通过调节实验条件而忽略，因此得到由于本底气体的碰撞（压力）而导致囚禁冷原子的损失率γ的值。通过下面的推导（囚禁原子的损失率与本底气体压力之间的关系），计算出本底气体的压力。冷原子损失率通常表示为：

式中：ni、σi、vi分别为第i类本底气体的分子数密度、碰撞截面和运动速度；σiυi为速度平均碰撞截面。粒子的碰撞截面大小反映了粒子发生碰撞的可能性大小。假定被囚禁的冷原子运动速度相比vi可以忽略，则碰撞截面σi可 以表示为：

典型MOT的势阱深度（D）一般在1 K量级，足够测量冷原子的碰撞截面[19-20]。对于范德瓦尔斯势场，可以简化碰撞截面公式为：

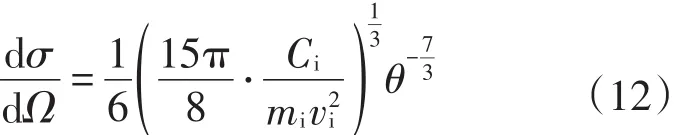
式中：dσ/dΩ为微分碰撞截面；dΩ为某个固定角；mi为与囚禁原子发生作用的第i类本底气体的分子质量；散射临界角为囚禁原子的质量。对式（12）积分可得碰撞截面：

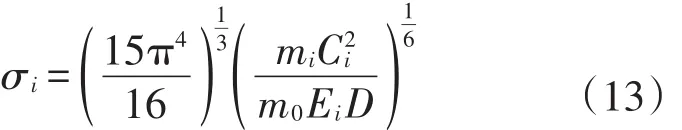
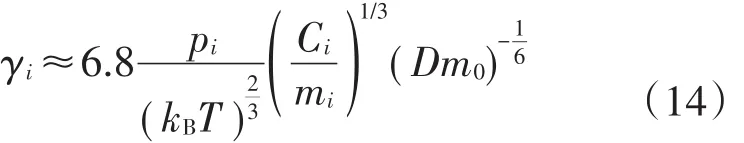
从式（14）中可以看到，只要测得原子损失率γi，就可以得出真空室中该类气体成分的压力。冷原子损失率与本底气体的Ci和mi相关，式中范德瓦尔斯力系数Ci可以利用Slater-Kirkwood公式估计出[21-22]：式中：me是电子质量；ai为本底气体i的电子极化率，ρi为其价电子数。式（15）中下标为零的各参量均为囚禁原子的相应参量，如ε0为冷原子的介电常数。

上述真空压力可以表示为：

从公式可以得出，真空度主要由冷原子与所有气体分子之间的碰撞损失率γi决定。

2 研究现状

2.1 国外研究现状

磁光阱已成为制备冷原子最重要的基本设备，广泛地应用于冷原子研究和应用中，如量子简并气体、冷碰撞、量子信息处理、超精密频率标准和量子光学的研究。在制造磁光阱之前，首要考虑的基本条件是制备和保持高真空，这与精确测量真空度密不可分[23-24]。

1988年美国贝尔实验室Bjorkholrn[20]首次进行了关于囚禁于磁光阱中的冷原子与气体分子碰撞的理论计算，建立超冷原子损失率（γx）与本底气体压力p的关系：

式中：n为本底气体分子数密度，n=p/kT，p为本底气体压力；Γ(x)为gamma函数；M为本底气体分子的相对分子质量；m为囚禁原子的相对原子质量；Cx为对应的常数；ax由公式 求出冷原子从势阱中逃逸出的最小能量为为势阱深度。

研究结果表明，冷原子与本底气体分子之间的碰撞是弹性碰撞。研究者同时定量计算了囚禁冷原子的寿命，但是该理论计算相对简单，简化了冷原子与本底气体相互碰撞过程，忽略了原子的激发态和基态与本底气体分子相互作用势的不同。此后，Bali等[21]和Góngora-T等[25]也进行了类似的相关理论计算。

2009年，加拿大英属哥伦比亚大学研究者[26-28]研究了磁光阱和磁阱中超冷Rb原子与本底气体（Ar）的碰撞过程，实验装置如图6（a）所示[26]。对Rb冷原子与本底气体碰撞展开了理论研究，并实验验证了冷Rb原子损失率与Ar气体分子数密度之间的关系，提出了一种测量冷原子碰撞截面的方法。如图6（b）所示，拟合数据结果呈直线性，直线的斜率就是平均速度损失率σRb,ArυAr，在磁光阱中（圆圈）的碰撞截面值小于磁阱中（方块）的，是因为磁光阱势阱深度（～1 K）远大于磁阱势阱深度（0.64 mK）。研究发现，改变激光失谐量等参数，不会影响碰撞截面的大小；利用经典散射与量子散射、L-J势函数等理论，通过分步法拟合计算，给出了冷原子与本底气体碰撞损失率、碰撞截面的理论计算公式；理论计算的碰撞截面、平均速度损失率结果与实验测量的结果基本吻合。

图6 冷原子真空测量装置示意图和Rb超冷原子损失率与室温下Ar气体分子数密度的关系图Fig.6 Schematic of CAVM and loss rate of trapped Rb versus room temperature argon gas density

2012年，美国佛吉尼亚大学Arpornthip等[29]理论计算了MOT囚禁的基态Rb原子与不同本底气体之间碰撞引起的损失率与本底气体压力的比值（γ/p），和被囚禁的基态碱金属原子与H2之间的γ/p值，如表1和表2所列[29]，相关理论见文章1.3部分。该理论计算结果与早期美国贝尔实验室Prentiss等[30]在Na原子的MOT中，本底气体主要是H2时，实验测得γ/p=3.8×105Pa-1·s-1的结果相一致；与加拿大英属哥伦比亚大学Fagnan等[26]和Dongen等[31]在MOT中测试Rb冷原子与Ar碰撞的结果基本吻合，分别为γ/p=1.2×105Pa-1·s-1和γ/p=1.7×105Pa-1·s-1。

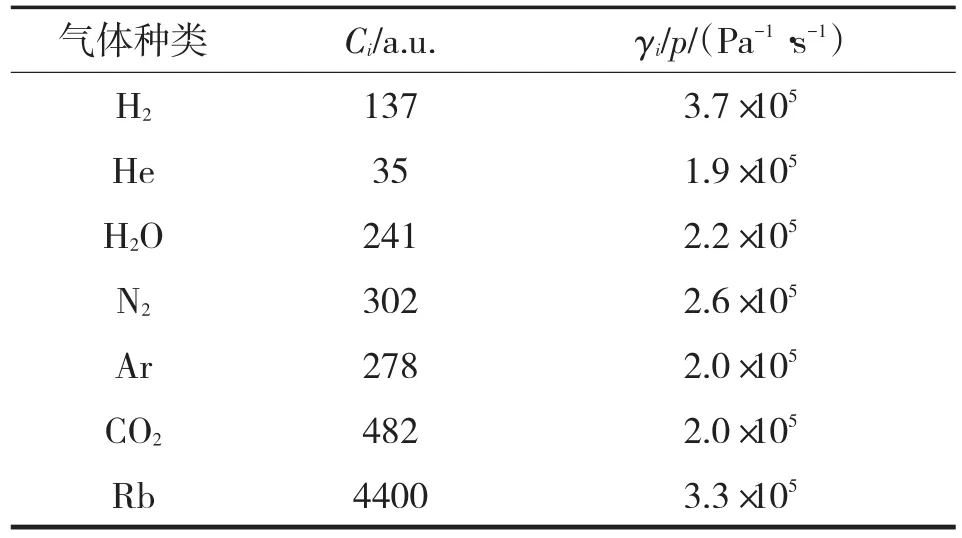
表1 基态Rb原子与本底气体碰撞损失系数的理论计算值Tab.1 Estimated loss coefficients for collisions between ground-state Rb atoms and the indicated gases

表2 基态碱金属原子与氢气分子碰撞损失系数的理论计算值Tab.2 Estimated loss rate coefficients for collisions between ground-state alkali-metal atoms and hydrogen molecules

Arpornthip等[29]也研究了MOT中冷原子的总损失率Г与压力p之间的关系：Γ=Γ0+aR+bp，Γ0为原子之间相互作用导致的囚禁原子损失率，即损失率βnˉ；a为热Rb原子碰撞引起的损失率；b为本底气体碰撞引起的损失率γ。通过降低装载率R，可忽略损失项aR的影响。在实验测试中，该种测量压力法的测量下限将受到双体损失项Г0的限制。假如bp小于Γ0，那么装载时间则与压力不相关。在原理上，Γ0=βnˉ可计算得出，然后从总损失率Г中减去，从而提高测量压力的测量下限。虽然β的值可以从实验测试和理论计算中获得，但是精确测量nˉ相对困难，而且β依赖于MOT的参数。在MOT中，采用蒸发法制备原子气体时，通过降低Γ0的值来降低测量下限是相当困难的。在该实验中获得的最低Γ0为0.013 s-1，则测量下限为3.3×10-8Pa。类似的Γ0损失率也被其他研究组报道，如1988年美国贝尔实验室Prentiss等[30]、2009年加拿大英属哥伦比亚大学Fagnan等[26]和1993年，日本电气通信大学Kawanaka等[32]得到的测量下限为3.3×10-8Pa；1995年，美国加州理工学院Willems等[33]在低温腔体中囚禁Cs原子，获得最低的MOT损失率为1 h-1，测量下限为6.7×10-10Pa。快速关闭激光法可以在实验中消除双体碰撞损失率Γ0。采用该方法，首先在MOT中装满囚禁原子，随后快速关闭激光，装载过程将停止，最后观测冷原子数的衰减过程。衰减过程的起启始段可能是非指数衰减，但是随着冷原子密度的减小，衰减过程呈指数变化。拟合指数衰减过程，可直接确定本底气体引起的损失率γ。如Prentiss等[30]采用该种方法研究了囚禁原子的损失率。Arpornthip等也研究了激光参数对冷原子衰减率的影响，结果发现，当激光束直径小到1.5 cm，或者磁场梯度在5.0×10-4～1.0×10-5T/cm之间时，激光参数对冷原子衰减率没有影响。另外，采用两种不同的激光冷却装置（不同的真空系统、激光参数和光学器件等），测试的实验结果基本一致，证实了冷原子真空计量技术在不同实验装置中具有一定的可靠性和推广性。

2015年，英国圣安德鲁斯大学Moore等[34]在Arpornthip等[29]的工作基础上进行了进一步研究，利用图7所示的冷原子装置[34]，在玻璃室中制造MOT，以87Rb原子作为囚禁原子，囚禁原子数采用光电二极管收集荧光来测量。为了区分热Rb原子和真空室内本底气体分别对冷Rb原子碰撞引起损失的贡献，将冷Rb原子囚禁动力学近似为式（18）速率公式[35]：

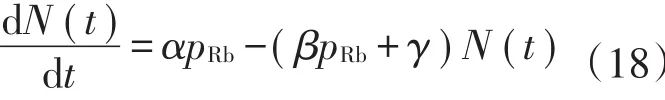
式中：αpRb为原子被俘获的速率，常数α代表MOT囚禁截面；pRb为热Rb原子分压力；( )βpRb+γ N(t)为囚禁原子的损失率，其中βpRbN描述了冷原子与热Rb原子碰撞引起的损失，γN描述冷原子与真空室内本底气体碰撞引起的损失。

式（18）的解为：

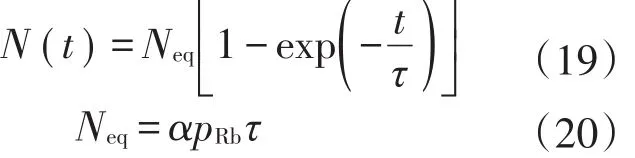
装载时间：

装载时间和冷原子寿命相一致。结合式（20）和式（21），消去pRb，则：

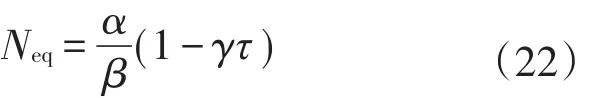
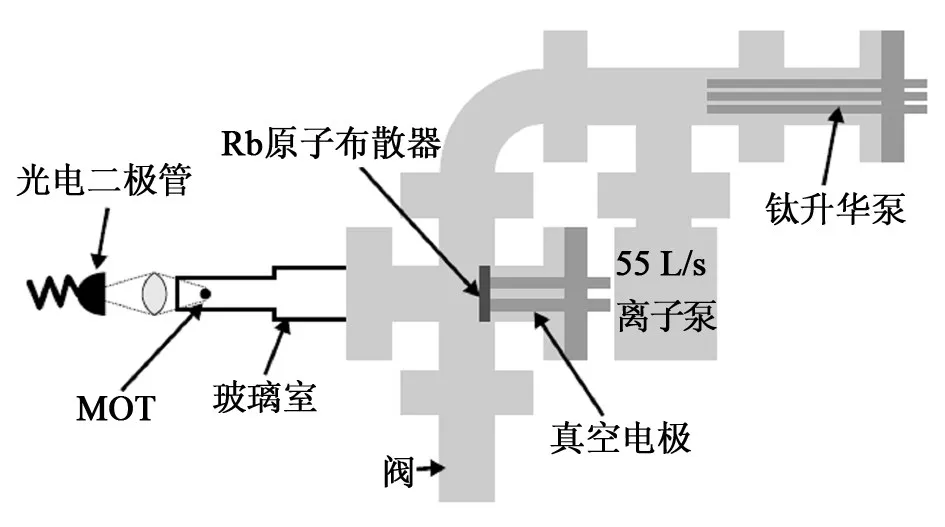
图7 冷原子装置示意图Fig.7 Schematic diagram of cold atomic device

在一定真空压力下，调节Rb源蒸发电流大小改变进入MOT中的热Rb原子数量，测量MOT中冷Rb原子装载曲线，通过拟合该曲线获得Neq和装载时间τ的Neq-τ曲线，如图8所示[34]。图8（a）是不同pRb下，MOT的装载曲线；图8（b）是Neq-τ图，图中圈起来的数据点为拟合图8（a）曲线获得的数据。总之，用Neq-τ图定性了本底气体与冷原子碰撞损失率的三个参数：MOT囚禁截面、冷原子与本底气体的碰撞损失率、冷原子与热Rb原子的碰撞损失率。由此可见，当改变真空室气体压力，真空室内的本底气体与冷原子碰撞引起的损失γ可通过变化式（22）计算出：

根据理论计算结果：γ/p=3.7×105Pa-1·s-1，可计算出此时的真空压力。

最后，利用这种冷原子真空测量方法评价了真空系统的出气行为。这不但证实了冷原子真空测量方法的可行性，而且相比传统电离规等测量方法，冷原子真空测量方法的优点是可以原位测量真空气体压力。

图8 MOT的装载曲线和Neq-τ图Fig.8 Construction of the Neq-τ plot with the MOT loading and the resultant Neq-τplot

2017年，美国国家标准与技术研究院（NIST）启动了一个基于超冷原子的真空标准（CAVS）项目研究[14，36]，测量压力范围从超高真空延伸至极高真空。CAVS采用磁光阱冷却的冷原子（如碱金属Li原子）作为传感原子，真空压力测量是通过测量冷原子的平均碰撞截面和测量冷原子损失率来实现。计划采用量子化学计算出冷原子Li和H2（Li+H2）电子系统的速度碰撞截面συ，再测量出冷Li原子与H2碰撞损失率，根据关系式：

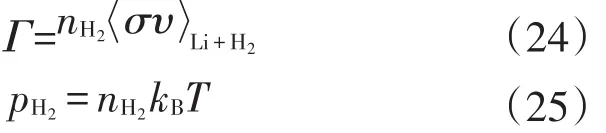
用计算得出的氢气压力（pH2）校准流量计，利用校准好的流量计和冷原子真空计测试其他系统的气体压力pother，计算Li原子和其他气体系统（Li+other）的碰撞散射截面：

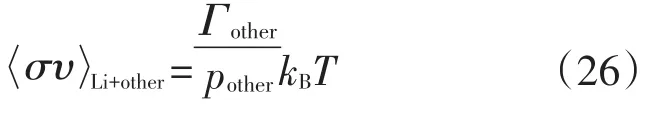
在此基础上，扩展到其他冷原子和其他气体系统中，如Rb+H2系统或Rb+其他气体系统，但是这种方法依然依靠传统手段，并受限于气体种类。

图9、10是NIST的研究人员提出的CAVS结构示意图和装置原型设计图[14，36]，该系统主要包括Rb原子布散器、预冷囚禁区、探测囚禁区、隔离区、待测真空系统等。

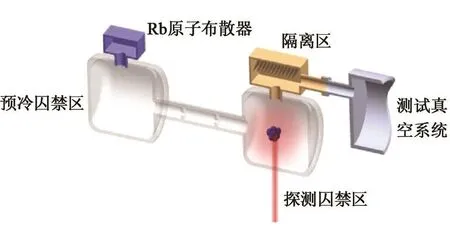
图9 冷原子真空标准（CAVS）结构示意图Fig.9 Schematic of the cold-atom vacuum standard（CAVS）

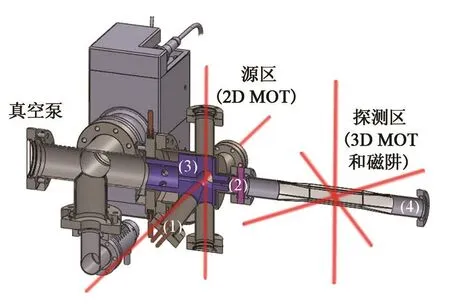
图10 CAVS腔体的剖面图Fig.10 Cutaway view of CAVS chamber

首先利用激光冷却方法将Rb原子在预冷囚禁区冷却到mK以下，之后转移到探测囚禁区。利用诸如激光诱导荧光等技术测量探测囚禁区Rb原子数目随时间的变化，通过Rb原子损失速率来测定待测真空体系的压力。挡板隔离区有两个作用：第一，阻止没有在预冷囚禁区被囚禁的室温Rb原子进入探测囚禁区；第二，阻止Rb原子进入待测的真空系统中。根据这一原理，有可能将CVAS装置缩小到芯片量级尺寸，应用到诸如航天器等需要高性能、轻量化、微型化装置的领域中。

2.2 国内研究现状

山西大学贾锁堂研究组[37]在Arpornthip等[29]的工作基础上也提出了类似的测量真空度的方法。从理论上计算了常见碱金属和碱土金属与本底气体碰撞的p/γ数值，如表3所列[37]。在实验研究中，实测了冷原子与本底气体碰撞引起的损失速率γ与真空度的函数关系，囚禁原子损失率γ与本底真空度呈线性关系，如图11所示[37]，数据点是实验测试值，实线是实验值的线性拟合结果，与理论计算值相吻合。

表3 常见碱金属和碱土金属的理论计算p/γ值Tab.3 Calculated p/γ for CommonAlkali Metals and Alkaline Earth Metals

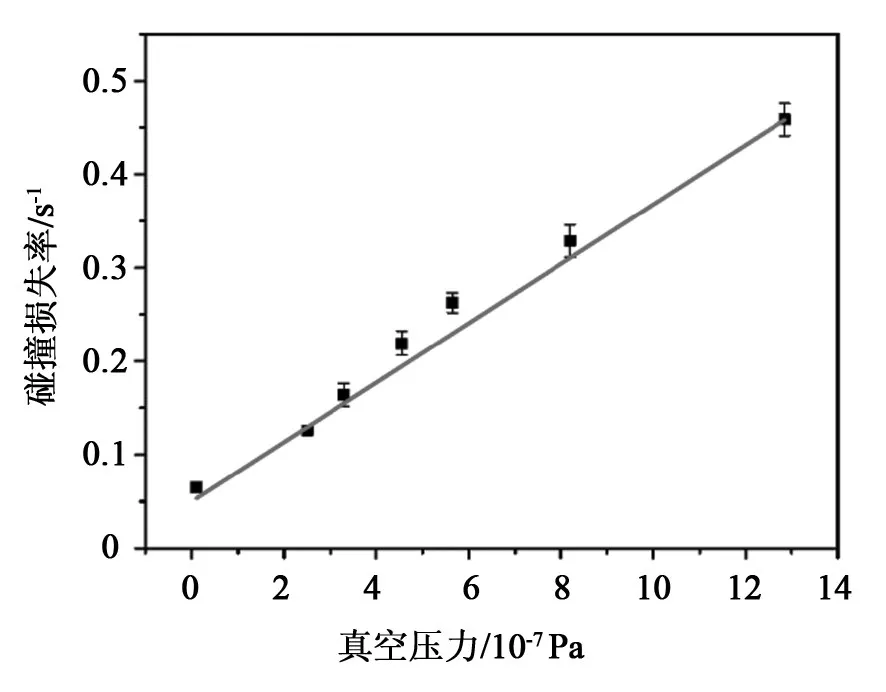
图11 冷原子与本底气体碰撞引起的损失速率γ与真空压力的函数关系图Fig.11 Rate constant for loss due to collisions with cold atoms and background gases γ as a function of vacuum pressure

此外还研究了激光参数对p/γ的影响，研究发现：p/γ的变化不依赖于激光强度、调谐、光束大小和磁场梯度的变化，如图12所示[37]。该种测量真空压力的方法也适用于其他碱金属和碱土金属原子，且满足商业应用的微型化需求。

图12 p/γ与再抽运激光强度和磁场梯度的函数关系图Fig.12 Proportional coefficient p/γ as a function of repumping laser intensity and magnetic field gradient

2018年，中国科学院上海光学精密机械研究所研究组[38]从理论和实验上研究了空间冷原子钟中的87Rb冷原子在MOT中和自由飞行过程中与本底气体碰撞引起的损失率与真空室气体压力的关系。图13是UHV腔体结构示意图[38]，该装置运行于微重力环境中，冷原子自由飞行时，依次穿过选择区、Ramsey作用区、探测区。调节离子泵阀门，改变真空压力，记录冷原子在不同本底气体压力下的MOT装载过程和冷原子云飞行时间。用残余气体分析仪测试真空室本底气体种类和分压力。在冷原子自由飞行过程中，没有热Rb原子与其碰撞，只有本底气体与其碰撞引起的损失，且在冷原子飞行过程中没有势阱深度。理论计算了冷原子在自由飞行时与本底气体碰撞的损失率。

图13 UHV腔体结构示意图Fig.13 Schematic of the UHV chamber

表4为理论计算的冷原子在MOT中和自由飞行过程中损失率与本底气体压力的关系γ/p[38]。实验测试了冷原子损失率与真空度之间的关系，如图14所示，实验结果和理论计算结果相一致。

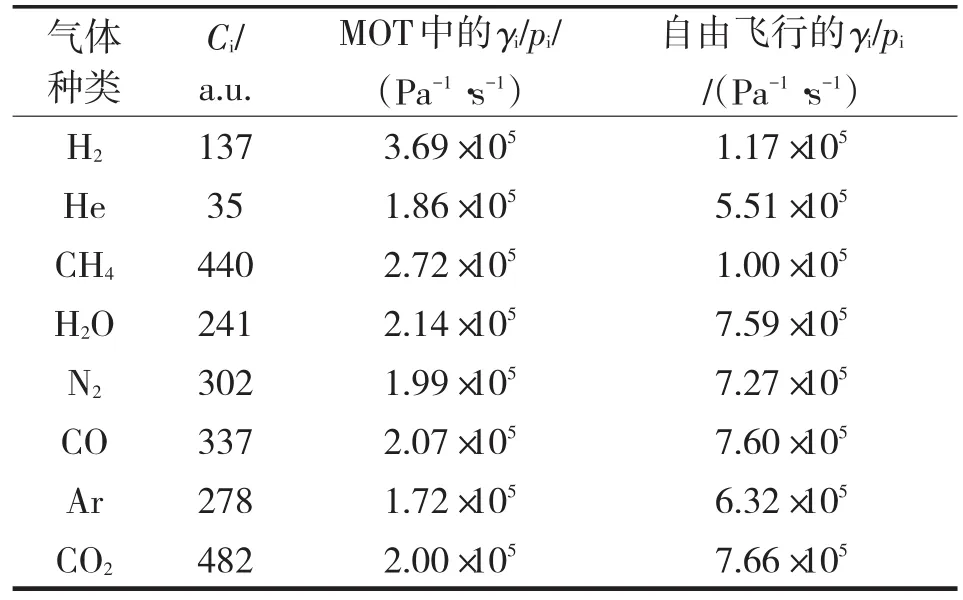
表4 冷Rb原子与本底气体碰撞损失系数的理论计算值Tab.4 Calculated loss coefficients for collisions between cold Rb atoms and the residual gases

实验证实：冷原子云自由飞行过程中因扩散引起的损失可以忽略。分析发现，在冷Rb原子云自由飞行过程中，未冷却的热Rb原子与冷Rb原子碰撞引起的冷原子的损失很小。因此，冷原子云自由飞行过程中发生的损失仅仅是由本底气体碰撞引起的。从实验和理论上研究了不同的真空度下冷原子的相对损失率，即冷原子云在MOT中的损失率与自由飞行时的损失率之间的比值，如图15所示[38]。在图中，数据点代表实测相对损失系数，虚线是理论计算结果，可以看出实验结果和理论计算结果相一致。

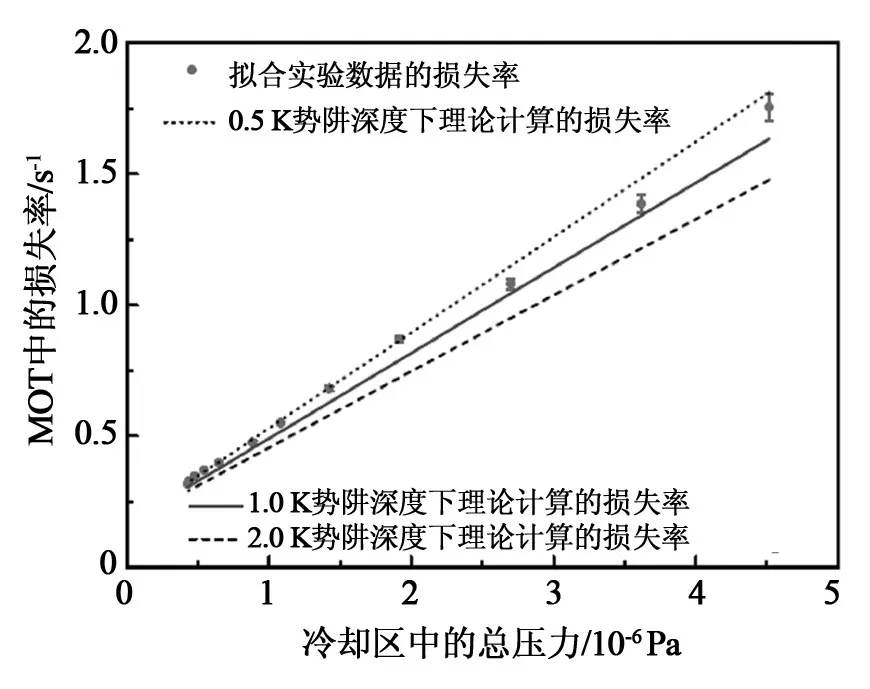
图14 MOT中的损失率与本底气体压力的关系图Fig.14 MOT loss rate versus pressure of residual gases

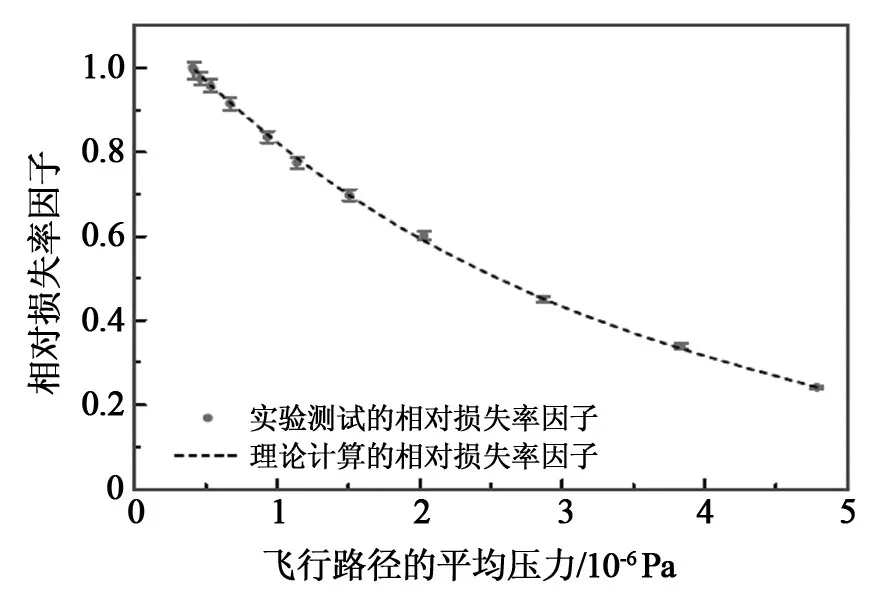
图15 相对损失率与飞行过程中本底气体压力的函数关系图Fig.15 Relative decay factor for cold atoms as a function of pressure

3 总结与展望

本文介绍了激光冷却原子的概念及囚禁原子的磁光阱的工作原理和结构。介绍了冷原子量子真空计量技术的基本原理，分析了该技术在国内外研究现状。利用超冷原子与本底气体碰撞的损失率测量真空的技术有几个优点：测量压力范围在超高/极高真空（10-4～10-10Pa），甚至更低；可原位测量本底气体压力；冷原子的损失率只依赖于原子与气体的碰撞截面以及对温度和时间的测量。因此，该技术有望发展成为新一代真空计量技术，进一步形成超高真空计量标准。亟待解决的问题有：

（1）虽然目前已有研究组完成了冷原子损失率与真空度的比值（γ/p）的理论计算，但是计算过程进行了简化，忽略了原子的激发态和基态与本底气体相互作用势的不同，因此，有必要采用新方法进行深入的理论计算。

（2）关于冷原子损失过程及不确定度的理论和实验研究较少。冷原子的损失由不同粒子碰撞引起，主要包括本底气体碰撞、冷原子双体或多体碰撞、热原子碰撞、激发态冷原子碰撞等。研究如何减少或消除非气体碰撞的影响是提高测量精度的关键，例如在仪器中加入易于吸收热原子的材料；或者采用紫外照射法产生热原子的装置，减少热原子对测量的影响；或者采用磁阱而不是MOT，可消除激发态原子等。

（3）并不是每次气体分子与冷原子碰撞都造成冷原子损失，所以碰撞散射截面并不等于碰撞损失散射截面，因此需要进一步研究碰撞散射截面和碰撞损失散射截面与势阱深度关系，寻找他们之间的碰撞统一规律。

总之，随着关键技术的解决和冷原子装置的微型化（芯片尺寸）、商业化、普及化，这种新型量子真空计量技术有望应用到诸如航天器等需要高性能、轻量化、微型化装置的领域中，我国应尽快开展此项技术的研究。