基于热特性的凸轮转子叶片马达密封间隙优化
2019-07-03朱彦楠陶建峰王旭永
张 强, 朱彦楠, 陶建峰, 王旭永
(上海交通大学 机械与动力工程学院, 上海 200240)
叶片马达具有体积小、转动惯量低、响应速度快、低速性能好等优点,适用于对动态及稳定性能有一定要求的工程应用场合[1-3].凸轮转子叶片马达(CRVM)是在凸轮转子叶片泵的基础上改进而来,其结构工艺简单、工作寿命长、输出转矩基本恒定、瞬时流量脉动小、噪声低,适用于对速率脉动、响应速度、质量等有严格要求的场合[4].
由于液压油的物理特性受温度影响较大,故液压系统在使用时需考虑其对温度的敏感性.液压伺服系统的发热来源主要包括节流损失和机械损失[5].在液压系统中,虽然各类阀体因节流损失而产生的热量占系统总产热的比重较大,但这部分热量在液压油流过CRVM内部时将被一起带走,并不会造成液压油温度的急剧上升.而在CRVM内部的密封间隙处,泄漏和摩擦产生的热量由于不能及时向循环油液传导,容易造成局部温度过高,甚至可能使液压油的黏度等理化性质发生改变,进而影响液压系统的正常工作.
因此,本文针对CRVM密封间隙局部的发热特性,提出凸轮与定子之间以及凸轮与隔板之间密封间隙的优化设计,并通过相关模拟和初步实验来验证其有效性.
1 CRVM的结构及工作原理
CRVM包含2个在空间上正交的凸轮转子,它们通过平键与主轴相连.凸轮的长径与定子内孔为滑动间隙配合,这种配合方式使CRVM具有低摩擦性和良好的低速防爬行性能[6].当凸轮转子旋转时,两对叶片在定子内部的叶片槽内作径向往复运动.2个凸轮被隔板分割成2个密封腔.由于叶片根部减压油的作用,使得叶片与凸轮转子能够紧密接触,进而将高压腔与低压腔分隔开.每转1圈CRVM可完成吸、压油2次.CRVM的具体结构原理图参见文献[7].
由文献[8]可知,CRVM宜选用二次余弦曲线作为凸轮转子的轮廓曲线.设凸轮宽度为Bc.凸轮转子的轮廓曲线包括半径为R的2个大圆弧和半径为r的2个小圆弧,以及4段过渡曲线.大小圆弧所对应的中心角均为β,每段过渡曲线的中心角均为α,且α+β=π/2.
2 CRVM密封间隙局部的发热机制
在系统工作时,压力损失、容积损失、机械损失等能量损失最终均会转化为热能,使得液压油的温度升高且黏度降低,进而导致CRVM的容积效率和工作效率均降低,甚至导致机械设备无法正常工作.CRVM的主要发热点有2处,分别位于凸轮与定子之间和凸轮与隔板之间.这些部位的用料均为钢材质,并不包含橡胶等其他密封介质,因此其理化性质和形位参数受温度影响较小.但是,温度的升高对密封间隙处的液压油理化性质影响较大,故下面将评估这2处关键发热点对液压油温度升高的影响情况.由于CRVM密封间隙处的液压油液尚未与腔体内的液压油混合,故将其温度升高的过程近似作为绝热过程处理.
2.1 凸轮与定子之间的密封间隙
凸轮与定子之间的流动可以简化为平板间的流动.假设液压油从高压腔泄漏到低压腔时所做的功及剪切流的摩擦做功均转化为内能,并且忽略过程中的热量损失;同时,在计算泄漏量和摩擦力矩时,为了简化计算过程,将液压油的密度、黏度、比热容等物理参数取常数值,忽略其取值随温度的变化.液压油从高压腔泄漏至低压腔,设温度变化量为ΔT1,由能量守恒方程可得
(1)
式中:Δp1=pa-pc,pa为高压腔压力,pc为低压腔压力;q1为凸轮与定子间的泄漏量;Ms为凸轮与定子间的摩擦力矩;ω为凸轮角速度;c为液压油的比热容,50 ℃时c=1.979 kJ/(kg·K);ρ为液压油密度,ρ=850 kg/m3.
基于平行平板间隙流动模型[9]计算凸轮与定子间的泄漏流量q1,并参考流体切应力计算模型[10]和文献[11]中对左右2个凸轮上对称摩擦力矩的处理方式计算得到Ms,代入式(1)可得
(2)
式中:δ1为凸轮与定子的间隙;μ为液压油的动力黏度;Bv为叶片宽度.
2.2 凸轮与隔板之间的密封间隙
导致凸轮与隔板之间泄漏的主要原因是压差流动,其过程如图1所示.

图1 压差流动示意图Fig.1 Differential pressure flow diagram
凸轮与隔板之间的油液温度升高原理与凸轮与定子之间的原理类似.液压油从高压腔经隔板泄漏至低压腔,设温度变化量为ΔT2,由能量守恒方程可得
(3)
计算左右凸轮与隔板间的泄漏流量之和q2,并根据凸轮的对称性[12],计算凸轮与隔板之间的摩擦力矩Mg,代入式(3)可得
(4)
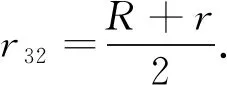
3 密封间隙温升模拟
CRVM运转时,密封间隙处的液压油既存在平行板间的压差流动,又存在由摩擦副相对运动引起的液体剪切流动.这两类流动都会造成能量的损失和局部温度的升高.随着密封间隙的增大,其相应的压差流动也越大,进而导致泄漏流量和节流能量的损失也越大,其相应的密封效果就越差.但同时,密封间隙越大,由剪切流动引起的发热量反而越小,且泄漏流量越大能促进液体吸收更多的发热量,使得局部温升相应减缓.
由式(2)和(4)可知,在CRVM的凸轮与定子、凸轮与隔板之间2个主要间隙密封处,其局部温度变化量ΔT主要与工作压力p、工作转速ω和密封间隙δ有关.因此,对于不同工作参数要求的CRVM,其密封间隙的设计指标也有所不同.在CRVM正常工作时,上述工作参数的取值范围分别为:2 MPa 表1 CRVM的相关参数Tab.1 Parameters of CRVM 用MATLAB软件对凸轮与定子间的温度变化量ΔT1进行仿真分析.首先,分析在不同的δ1和ω下,p对ΔT1的影响.当ω=120 r/min,δ1=8,10,12,14 μm时,ΔT1随p的变化曲线如图2(a)所示;当δ1=12 μm,ω=50,100,150,200 r/min时,ΔT1随p的变化曲线如图2(b)所示. 图2 不同ω和δ1条件下ΔT1随p的变化曲线Fig.2 The curves of ΔT1 along with p under different ω and δ1 由图可知,当δ1和ω取值不同时,随着p的增大,ΔT1先减小后增大,且当p=5 MPa时,除δ1=12 μm,ω=50 r/min的条件外,ΔT1均达到最小值.这是由于p较小时,泄漏流量较小,摩擦持续作用在一小部分液压油上,使得局部温度升高;当p过大时,泄漏造成的压差损失使油液的压力势能转化为内能而使局部温度升高.值得注意的是,图2(b)中红线左侧代表的低压力高转速的极端工况是极少出现的,因此可以不考虑这种工况下的温度升高对系统和油液的影响.总体而言,当2 MPa 当p=5 MPa,ω=50,100,150,200 r/min时,ΔT1随δ1的变化曲线如图3所示.由图可知,当δ1>15 μm时,δ1对ΔT1的影响较小;当δ1<8 μm时,ΔT1随着δ1的减小而急剧增大,且ω越大,ΔT1的增大效应越明显.这是由于δ1较大时,泄漏流量增大,摩擦产热不明显,压差损失的发热量与泄漏流量的比值为定值;而当δ1足够小时,泄漏流量减小,摩擦产热增大,局部温升效应尤为明显. 图3 不同ω条件下ΔT1随δ1的变化曲线Fig.3 The curves of ΔT1 along with δ1 under different ω 图4 不同δ1条件下ΔT1随ω的变化曲线Fig.4 The curves of ΔT1 along with ω under different δ1 当p=5 MPa,δ1=8,9,11,13 μm时,ΔT1随ω的变化曲线如图4所示.由图可知,ΔT1随ω的增大而升高,这是由于ω的增大加剧了摩擦产热现象.在CRVM工作时,假设有油冷机保证油源温度为恒定室温(约为20 ℃),为了防止液压油的黏度发生改变,进而影响CRVM的正常工作,应保证油液温度低于50 ℃,即ΔT1<30 ℃.在ω=200 r/min的条件下,当δ1=8 μm时,ΔT1约为50 ℃,远超过临界值30 ℃;当δ1=9 μm时,ΔT1约为30 ℃;当δ1=11 μm时,ΔT1约为10 ℃;当δ1=13 μm时,ΔT1则更小.与液压系统各阀口节流损失的发热功率相比,密封间隙处的发热功率占比不大,追求过小的ΔT1是没有意义的,反而会由于δ1过大导致CRVM的综合效率降低,因此从防止局部温度过高和提高CRVM综合效率的角度而言,δ1的最佳取值范围为9~11 μm. 采用与上一节相同的研究方法,分析凸轮与隔板之间的温度变化量ΔT2. 当ω=120 r/min,δ2=8,10,12,14 μm时,ΔT2随p的变化曲线如图5(a)所示;当δ2=12 μm,ω=50,100,150,200 r/min时,ΔT2随p的变化曲线如图5(b)所示.由图可知,当δ2和ω取不同值时,随着p增大,ΔT2先减小后增大.当p=3 MPa时,除δ2=12 μm,ω=50 r/min条件外,ΔT2均达到最小值.在常规工况下,ΔT2对p的变化并不敏感.与凸轮与定子之间的温度变化量相比,在同样的p、ω和δ条件下,ΔT2<ΔT1. 图5 不同ω和δ2条件下ΔT2随p的变化曲线Fig.5 The curves of ΔT2 along with p under different ω and δ2 当p=5 MPa,ω=50,100,150,200 r/min时,ΔT2随δ2的变化曲线如图6所示.由图可知,凸轮与隔板之间同样存在δ2过小时局部温度陡升的情况.这是由于当δ2过小时,凸轮与隔板之间的泄漏流量减小,同时摩擦产热增加,导致局部温升比较明显.因此,为了防止局部过热应重点控制δ2. 当p=5 MPa,δ2=6,7,8,9 μm时,ΔT2随ω的变化曲线如图7所示.由图可知,ΔT2随ω的增大而增大.在ω=200 r/min的条件下,当δ2=6 μm时,ΔT2约为50 ℃,远超过临界值30 ℃;当δ2=7 μm时,ΔT2约为30 ℃;当δ2=8 μm时,ΔT2约为12 ℃;当δ2=9 μm时,ΔT2则更小.从防止局部温度过高和提高CRVM综合效率的角度而言,δ2的最佳取值范围为7~8 μm. 图6 不同ω条件下ΔT2随δ2的变化曲线Fig.6 The curves of ΔT2 along with δ2 under different ω 图7 不同δ2条件下ΔT2随ω的变化曲线Fig.7 The curves of ΔT2 along with ω under different δ2 CRVM的性能指标主要有输出转矩和综合效率.输出转矩主要与p和转子尺寸有关,几乎不受δ影响;综合效率η是容积效率ηv与机械效率ηm的乘积,这一指标与δ的关系可参考文献[13].其研究结果表明,当δ=10~15 μm时,η最高(约为85%),即基于热特性间隙优化原则选取的最优间隙同样能够提升CRVM的综合效率. 搭建一套CRVM电液伺服系统,该系统通过上位机和下位机双计算机控制模式对CRVM进行控制.CRVM电液伺服系统的控制原理如图8所示. 在CRVM实验系统中,上位机输出的控制指令经过下位机的运算处理,将输出的电压控制信号经过伺服放大器转换为电流控制信号后输入电液伺服阀并控制伺服阀阀芯的位移,伺服阀输出高压液压油驱动CRVM旋转,从而带动负载运动.基于接触式温度表的CRVM伺服系统的热特性实验装置实物如图9所示. 图8 CRVM伺服系统热特性原理图Fig.8 Schematic of thermal characteristics of the CRVM system 图9 CRVM伺服系统热特性实验装置侧面图Fig.9 Side view of test rig of the CRVM servo system 在实际工作时,电动机和液压泵的运转会不可避免地为CRVM伺服系统引入大量热量,同时伺服阀的节流损失也都将转化为热量,造成伺服系统温升较快.因此,若只是简单地测量CRVM的表面温度Tm,无法对由于其自身运转产生的热量对CRVM造成的温升影响进行研究.本文设计了一种实验方案,即分别记录油箱温度To和CRVM的表面温度Tm,待温度稳定(120 min)后,以(ΔTm-ΔTo)表征排除系统其他热源后CRVM自身运转产生的热量对Tm升高造成的影响. 在实验过程中,p=5 MPa,电液伺服阀全开.首先使CRVM连续回转运行(ω=60 r/min),分别记录To和Tm的数值.待系统冷却后,再将CRVM负载盘卡住,使CRVM处于堵转状态,再次记录To和Tm的数值.实验结果记录如表2和3所示. 表2 回转状态下油箱和CRVM的温度变化情况表 表3 堵转状态下油箱和CRVM的温度变化情况表 在回转状态下,CRVM的转子、定子、叶片的摩擦以及密封间隙处的泄漏都会产生热量,使Tm升高;而在堵转状态下,只有泄漏会造成发热量.由表2和3可知:待温度稳定后,在回转状态下,Tm比To高约 2.6 ℃;在堵转状态下,Tm比To高约 0.9 ℃.这与图8(b)中,当δ1=12 μm,p=5 MPa,ω=50 r/min时,ΔT1约为3 ℃的模拟结果是一致的.同时,实验结果也验证了影响CRVM温度升高的因素中,摩擦因素比泄漏因素占更大比例这一结论. (1) 过高或者过低的工作压力p都会导致CRVM密封间隙处的温度变化量ΔT较大;当p=3~5 MPa时,ΔT较小.在一般工况下,ΔT对p的变化并不敏感. (2) 当密封间隙δ>15 μm时,δ对ΔT的影响十分微弱;而当δ<8 μm时,ΔT会随δ的减小而急剧增大,且工作转速ω越大,此增大效应越明显.因此,实际工作中应严格控制凸轮与定子及凸轮与隔板之间的制造和装配精度,防止因间隙过小造成局部过热,最终影响CRVM的正常工作. (3) 在p、ω和δ取值相同的条件下,ΔT1大于ΔT2. (4) 为了保证液压油良好的工作状态,应控制CRVM的ΔT不超过30 ℃,这就要求CRVM的δ不可过小.研究表明过大的δ对控制ΔT的升高没有意义,因此从防止局部过热和提高CRVM的综合效率角度而言,δ1的取值范围为9~11 μm,δ2的取值范围为7~8 μm.
3.1 凸轮与定子之间的温升模拟



3.2 凸轮与隔板之间的温升模拟
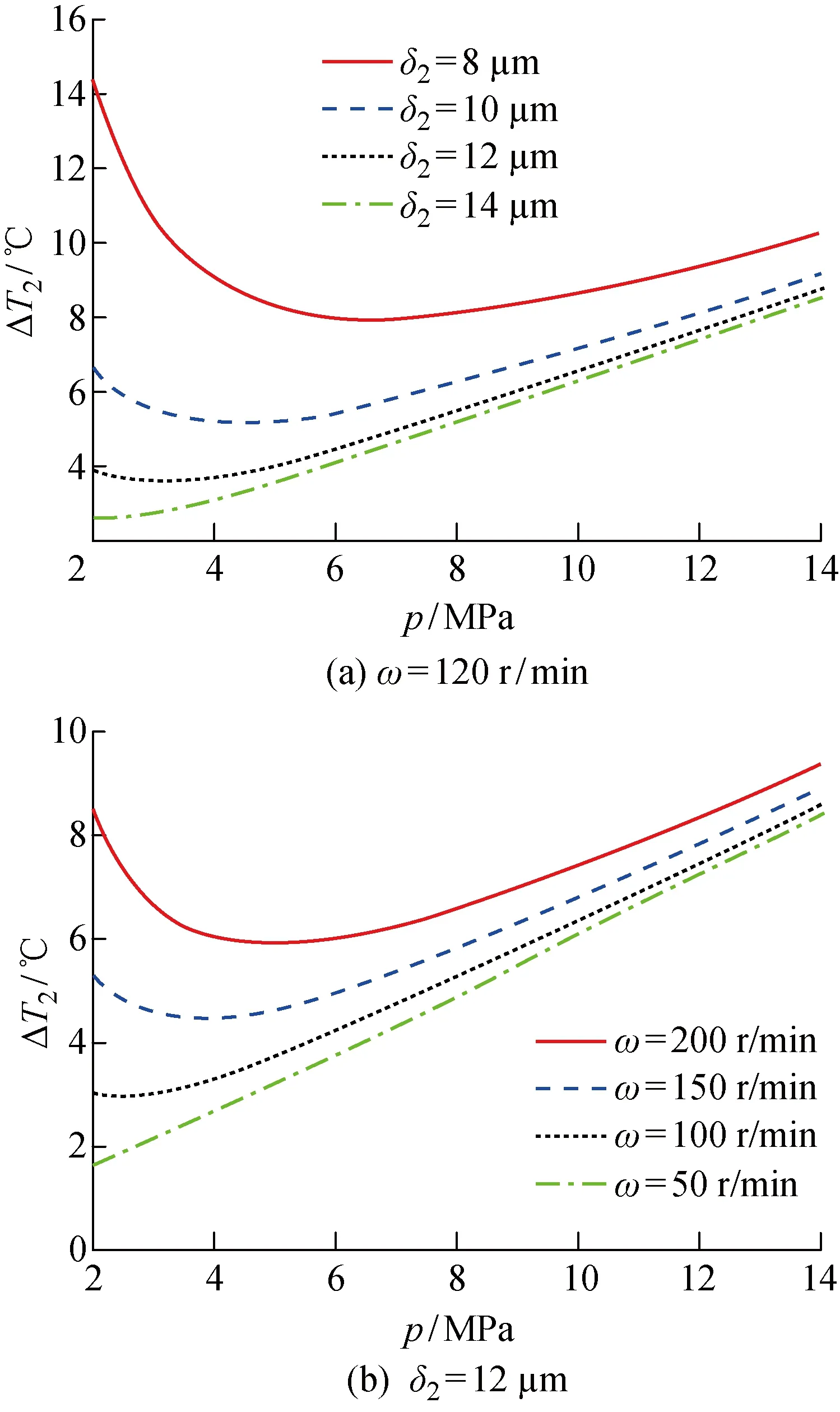
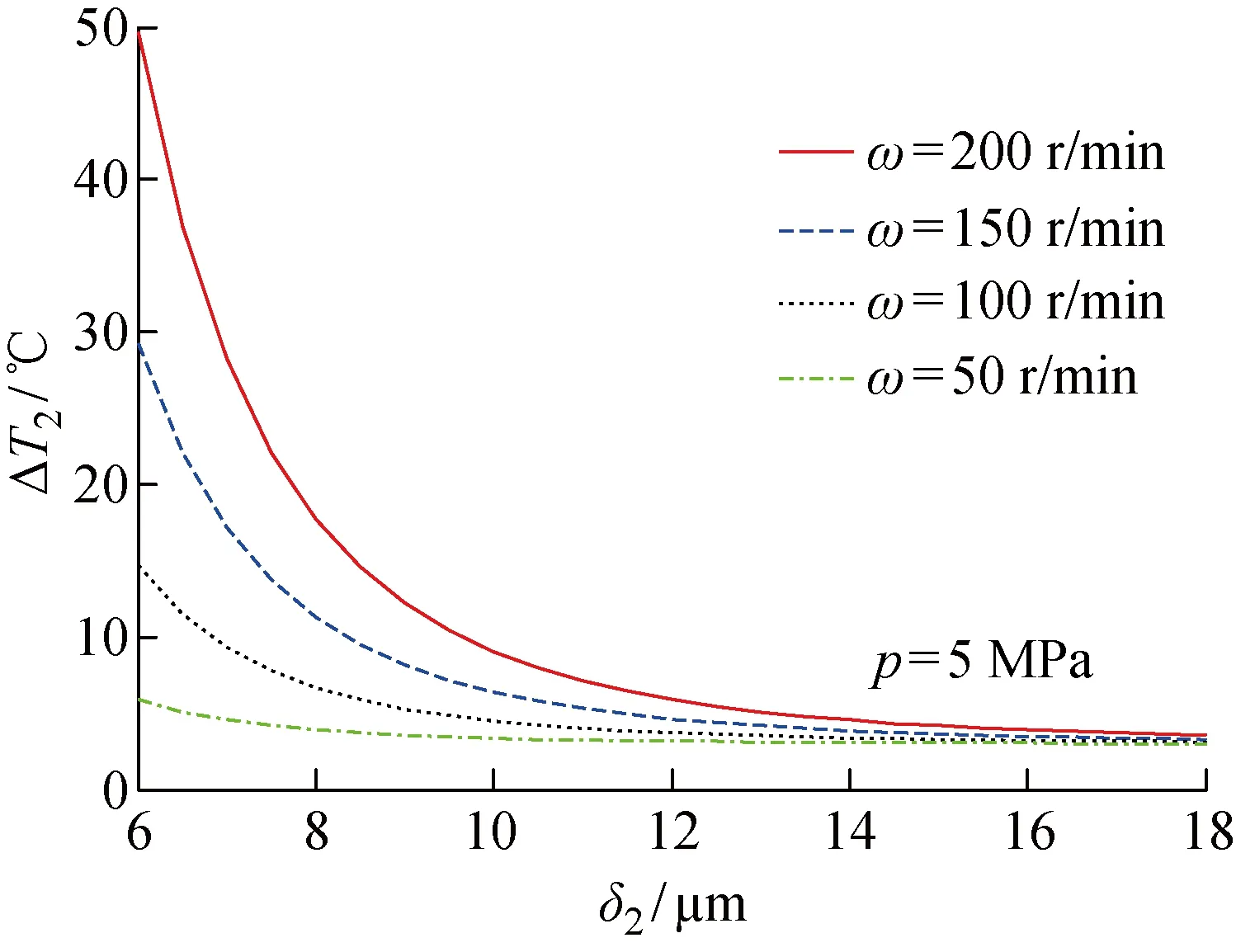

4 CRVM的温度变化对比实验




5 结论
