基于剪切稀化效应的血液流体-扩张血管耦合模型的血管损伤分析

江旭东， 李鹏飞， 刘 铮， 滕晓艳

(1. 哈尔滨理工大学 机械动力工程学院， 哈尔滨 150080； 2. 哈尔滨工程大学 机电工程学院， 哈尔滨 150001)

人体血管支架植入术已成为治疗动脉粥样硬化的有效手段.但是，血管支架的介入，使得血管斑块处于高应力状态，改变了血管近壁面血液流动的力学性能，在血管扩张区形成壁面峰值等效应力和峰值切应力以及低壁面切应力区，还有可能引起斑块脆性断裂和血管内膜细胞增生而出现血管再狭窄问题[1-2].因此，建立狭窄血管-支架-血液耦合系统的动力学模型，分析血管动脉粥样硬化损伤的力学性能参数，探讨斑块易脆性和血管再狭窄等损伤性能，对于抑制血管损伤和优化治疗流程具有重要意义.

为了研究支架植入过程中血管内皮的损伤程度，文献[3-4]中通过建立支架-血管-斑块耦合系统的非线性有限元模型，分析了血管与斑块组织的应力场，并以血管壁面的峰值等效应力作为斑块破裂和血管内膜细胞增生等介入性损伤的评定参数.另外，从生物力学的角度来看，支架作用的生理环境是血管壁和血液，因此，血液流动力学性能参数是影响动脉粥样硬化和斑块形成与发展的另一个关键因素.研究表明，对于狭窄血管[5-6]或支架-血管耦合系统[7-9]与血液的流-固耦合模型，可将血管腔内壁模型简化为理想的圆柱面，以分析流-固耦合界面的应力场；较低的壁面切应力有助于血管内膜细胞增生并形成斑块，较高的壁面切应力可能引起斑块的脆性断裂.但是，在血液流动力学模拟中，将血液简化为牛顿流体，忽略了血液黏度随剪切速率增大而减小的剪切稀化效应，特别是在低速流动时血液的非牛顿性更为显著[10-11].Martin等[12]和Chiastra等[13]研究了扩张血管-血液的耦合作用机制，但忽略了血液的剪切稀化效应和人体血管曲率的影响；Chen等[14]研究了支架-分支血管流-固耦合系统的血液剪切稀化的流动特性，但忽略了支架、血管和斑块的相互作用，而且所用血液的动力学计算构型并非血管支架-狭窄血管的耦合扩张构型，从而影响了血管壁面应力和血液流动的预测结果，无法深入分析血管的生物力学损伤情况.鉴于此，本文在考虑人体真实血液的剪切稀化效应和人体血管曲率影响的前提下，构建了血液-扩张血管的耦合动力学模型，通过血管的斑块峰值应力、壁面峰值切应力及其峰值等效应力的变化来分析狭窄血管的结构应力场和血液的流动力学特性，并探讨了支架介入对血管和斑块组织断裂及血管再狭窄等生物力学损伤的影响.

1 血管支架介入系统

在临床实践中，血管支架的介入过程分为压握阶段、自由扩张阶段以及接触斑块后与病变血管耦合扩张阶段.由此，本文构建的血管支架介入系统有限元模型包含压壳、支架、球囊、血管和斑块等结构与生物组织部件(如图1所示).压壳与球囊部件采用4节点线性减缩积分壳单元离散，支架、血管与斑块部件采用8节点增强型沙漏控制的线性减缩积分的实体单元离散.

图1 血管支架介入系统有限元模型Fig.1 Finite element model of implantation system for a vascular stent

病变血管的曲率半径为6 mm、内径为3 mm，健康血管的壁厚为 0.9 mm、狭窄率为40%(斑块最大壁厚 0.6 mm).S型血管支架(单个正弦波形连接筋)与N型血管支架(1.5 个正弦波形连接筋)支架单元长度均为 3.75 mm、外径均为 1.54 mm、壁厚均为 0.12 mm，支撑体的长度与周向宽度分别为 1.44 和 0.15 mm，联接筋的长度与周向宽度分别为 0.87 和 0.06 mm，血管支架网格如图2所示.

图2 血管支架网格Fig.2 Meshed vascular stents

1.1 材料模型

由于血管支架介入过程所经历的塑性变形较大，故其材料模型采用双线性弹-塑性材料模型和基于J2流动律的等向屈服强化模型，并利用线弹性模型描述压壳将支架压握于球囊表面的弹性变形过程.采用基于3阶减缩多项式的应变能密度势函数描述健康血管与斑块的超弹性本构关系，并将球囊本构模型简化为1阶Mooney-Rivlin模型.从生物组织学的角度可将动脉粥样硬化斑块划分为低增生斑块、增生斑块和钙化斑块，其中钙化斑块为易脆性斑块，因此，本文将钙化斑块作为分析对象.表1所列为血管、斑块和球囊等组织的材料超弹性参数C10、C01、C20、C11和C30的取值[15]，血管支架和压壳的材料性能参数见表2[15].

表1 血管、斑块和球囊的材料超弹性参数Tab.1 Material hyperelastic coefficients of arterial tissue, plaque tissue and balloon

表2 血管支架和压壳的材料性能参数

Tab.2 Material coefficients of vascular stent and crimping tool

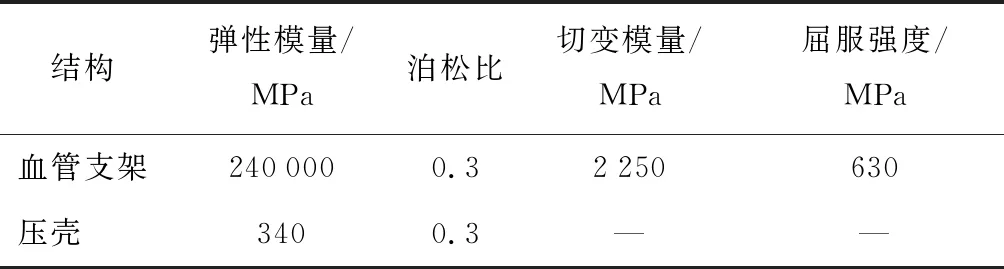
结构弹性模量/MPa泊松比切变模量/MPa屈服强度/MPa 血管支架2400000.32250630压壳 3400.3——

根据Lally等[16]的研究结果，假定血管和斑块组织满足不可压缩条件，则其应变能密度势函数可表示为

(1)

式中：I1、I2分别为右Cauchy应变张量C=FTF的第1、2不变量，F为变形梯度.

运用Green方法[16]推导所得不可压缩超弹性材料的应力-应变关系为

(2)

(3)

式中：S为第2 Piola Kirchhoff应力张量；I为2阶单位张量；σii为Cauchy应力张量σ的第1不变量，i为张量指标.

将第2 Piola Kirchhoff应力张量S转变为Cauchy应力张量σ，则有：

σ=FSFT

(4)

联立式(2)～(4)，则有：

(5)

式中：B=FFT，为左Cauchy应变张量.

1.2 控制方程

由于血管支架、血管和斑块具有不可压缩性，且其变形过程满足准静态条件，所以结构域的控制方程为动量平衡方程，即在t时刻的结构域Ωs(t)，有

(6)

在t时刻的结构边界Γs(t)，有

σs·n-f2=0

(7)

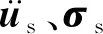
1.3 边界条件

在血管和支架的左、右断面分别约束轴向和周向自由度，在支架-压壳、支架-球囊和支架-血管界面定义接触约束，进而抑制两者沿周向和径向的刚体运动.在压握阶段，在压壳上施加径向均匀位移约束，将支架固定于球囊表面；在自由扩张和耦合扩张阶段，在球囊上施加径向均匀位移约束，将狭窄血管扩张至名义尺寸.

2 血液-扩张血管耦合模型的血液流动力学模拟

研究表明[17]，由于血管支架的展开及血管壁的钙化作用而导致扩张血管刚化，且血液流动作用下的扩张血管腔内构型变化微小，所以可将扩张血管视为刚体；此外，其对于血液流动力学特性无显著影响[13]，因此，本文忽略扩张血管的弹性变形，分析具有剪切稀化效应的血液流体与扩张血管耦合作用下的血液流动力学特性.

采用支架-狭窄血管耦合扩张得到的变形构型，通过计算构型的节点位置信息来重建扩张变形后的支架-血管耦合实体模型(如图3所示).同时，构建血液-扩张血管的耦合动力学模型，以分析具有剪切稀化效应的血液流体与扩张血管的相互作用机制，以及血管壁面切应力和等效应力对血管损伤的影响.

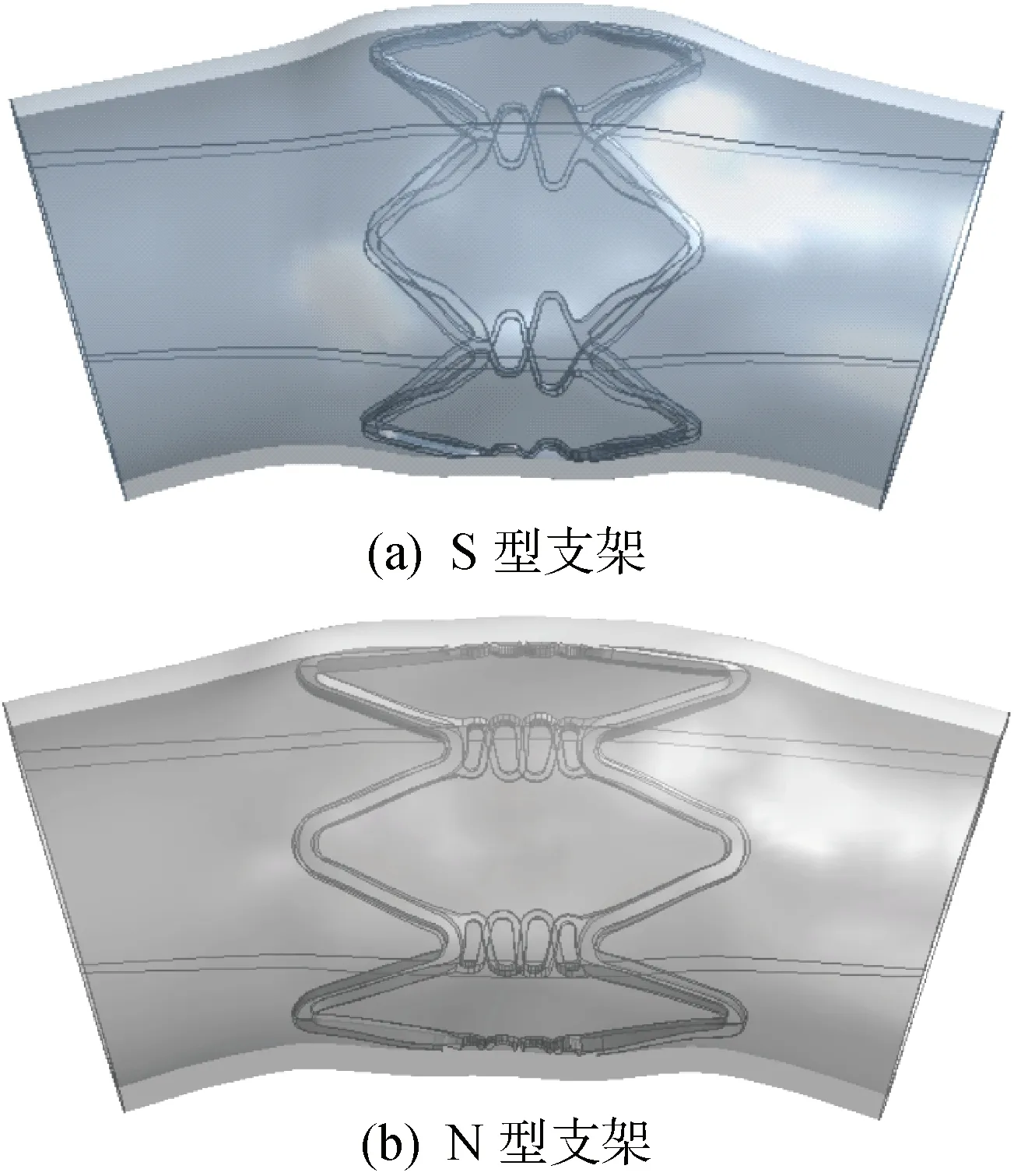
图3 重建的狭窄血管扩张构型Fig.3 Configuration reconstruction of expanded stenotic artery

2.1 材料模型

血液流体的黏度具有很强的剪切速率依赖性，特别是在血液流动速度很低时呈现出剪切稀化效应，它有助于产生较低的壁面切应力区域和较高的血管壁面峰值应力，进而促进血管动脉粥样硬化斑块的形成和发展.本文利用广义幂律模型描述具有剪切稀化效应的血液黏度，具体表达式为

(8)

(9)

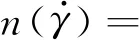
(10)

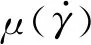
根据非线性连续介质力学理论，血液的剪切速率为

(11)

式中：vf为血液的流动速度矢量；εf(vf)为对称变形张量，可表示为

由此，联立式(7)～(11)，所得具有不可压缩剪

切稀化效应的血液流体的应力-应变关系为

(12)

式中：σf为流体的Cauchy应力张量；p为血液的压强.

2.2 控制方程

由于血液具有不可压缩性，故其流场控制方程可用非定常黏性流动的Navier-Stokes方程，即

(13)

式中：ρf为血液的密度.

2.3 边界条件

设置扩张血管左端入口条件为均匀且呈正弦波形变化的速度边界，速度峰值为 0.225 m/s，脉动频率为 0.8 Hz(人体心动频率)，出口相对压力为0，壁面条件为刚性无滑移边界.

2.4 性能指标

血管壁面切应力τw与动脉粥样硬化斑块的形成与发展密切相关，较低的壁面切应力(τw<0.5 Pa)将引起血管再狭窄，较高的壁面切应力有可能导致斑块的脆性断裂，它可以表示为

τw=-σf·n·τ

(14)

式中：τ为血管内壁的切向矢量.

Karimi等[6]发现，较高的血管壁面等效应力能够使得斑块面临壁面萌生裂纹的风险，并将扩张血管-血液的流-固耦合壁面处的等效应力表示为

(15)

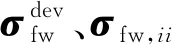
3 结果与分析

3.1 血管的斑块峰值应力

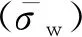
研究表明[2]，对于狭窄率为40%的低增生斑块，其峰值应力为 1.59 MPa，而本文计算所得S型支架的血管斑块峰值应力为 1.25 MPa、N型支架的血管斑块峰值应力为 1.11 MPa，与文献[2]中的结果基本一致.对比S型与N型支架产生的血管等效应力场和斑块峰值应力发现：S型支架对血管产生的力学刺激更显著；N型支架由于具有更优的纵向柔顺性，使其与血管的失配性较低，故其斑块峰值应力更小，具有更低的斑块断裂风险.

图4 狭窄血管的等效应力场Fig.4 Stress fields of stenotic artery

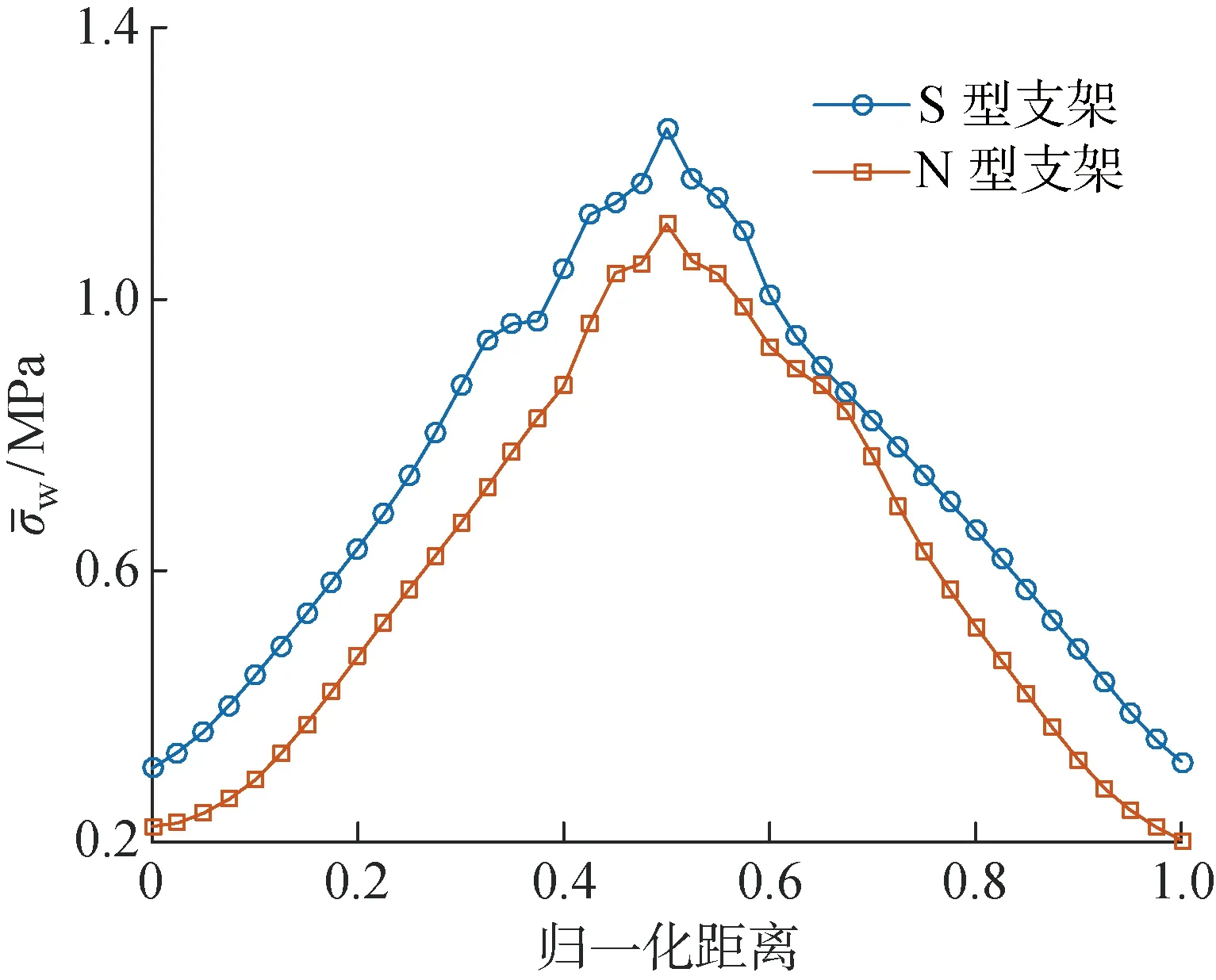
图5 斑块壁面的等效应力分布Fig.5 Equivalent stress distributions on plaque wall

3.2 血液的流动力学特性

本文采用有限体积法求解式(8)～(13)的计算流体动力学模型，以对比分析一个心动周期内不同时刻的血管壁面切应力、血流速度、壁面等效应力和压力等血液流动力学性能参数的变化情况，并通过对比S型和N型支架的血管斑块应力及血管壁面的切应力和等效应力，以分析血液流动力学性能参数对斑块易脆性和血管再狭窄等损伤性能的影响.

图6～8所示为一个心动周期内不同时刻的血管壁面切应力、血液的流动速度流线和速度场的变化情况.可见，在血管支架支撑体波峰和联接筋附近出现了较低的壁面切应力区域(τw<0.5 Pa)，从而加速了动脉粥样硬化斑块的形成和发展，导致产生血管的再狭窄问题；在血管扩张段中心区域形成了较高的壁面切应力区域(τw处于47～70 Pa)，使其易于产生斑块的脆性断裂.表3列出了两种支架的血管斑块峰值应力及血管壁面的峰值切应力和峰值等效应力.可见，采用本文模型计算的壁面峰值切应力分别为71 Pa(S型支架)和60 Pa(N型支架)，这与文献[18]中的计算结果(在忽略血管支架对狭窄血管的扩张作用下，狭窄血管的壁面峰值切应力为65 Pa)相符.由表3还可见，与S型支架相比，N型支架-血管耦合扩张构型在扩张段的低壁面切应力区域更小且壁面峰值切应力更低，从而降低了血管再狭窄和斑块破裂的概率.此外，N型支架具有较大的通流截面，有利于抑制血液垃圾在血管壁面的沉积，从而降低血管壁面增厚的可能性(见图7和8).

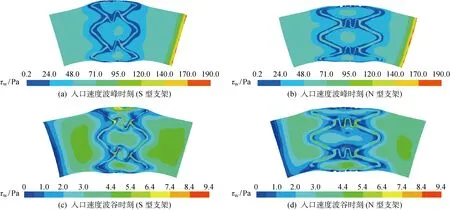
图6 血管壁面的切应力Fig.6 Arterial wall shear stresses

图7 血液流动的速度流线Fig.7 Velocity streamlines of blood

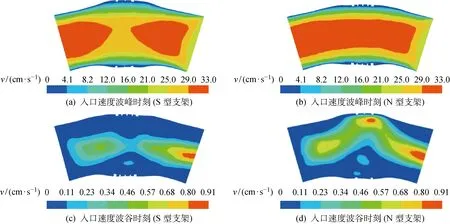
图8 血液流动的速度场Fig.8 Velocity fields of blood

表3 狭窄血管支架扩张段斑块和壁面的峰值应力

Tab.3 Peak stresses on plaque and wall in expanded subdomain of stenotic artery

支架斑块峰值应力/MPa壁面峰值切应力/Pa壁面峰值等效应力/kPaS型1.257113.87N型1.11608.41

图9和10所示为血管壁面的等效应力变化情况和支架与血管流-固耦合界面的压力场.可见，在血管支架联接筋附近出现了较高的血管壁面等效应力区域，使其易于产生斑块的脆性断裂.与S型支架相比，N型支架-血管耦合扩张构型的血管壁面峰值等效应力更小，因而能够降低斑块断裂的可能性.在一个心动周期内，入口速度波峰时刻的壁面压力场显著高于波谷时刻，这种短时间内的较大壁面压力变化易于导致动脉组织的退变受损(见图10).

综上所述，在血管支架支撑体几何形状相近的情况下，联接筋中正弦波形的个数对于弯曲血管的应力场和血液流动力学特性影响显著.具有单个正弦波形连接筋的血管支架(S型)与血管的失配性显著高于具有 1.5 个正弦波形连接筋的血管支架(N型)，使得S型支架介入引起的血管斑块峰值应力、血管壁面峰值切应力和峰值等效应力等参数均高于N型支架介入.因此，优化联接筋中正弦波形及波数，将有助于改善血管支架的生物力学性能，降低血管斑块出现脆性断裂的风险.

图9 血管壁面的等效应力Fig.9 Arterial wall equivalent stresses

图10 支架与血管流-固耦合界面的压力场Fig.10 Pressure fields on fluid-structure interface

4 结论

(1) 在血管支架介入过程中，在弯曲血管最狭窄处出现了较高的等效应力梯度区域，使其易于产生斑块的脆性断裂.与S型支架相比，N型支架的纵向柔顺性更高，使得斑块峰值应力更小，故其出现斑块断裂的风险更低.

(2) 在血管支架支撑体波峰和联接筋附近出现了较低的壁面切应力区域，使其易于产生血管内膜增生，并出现血管的再狭窄问题；而在血管扩张段中心区域形成了较高的壁面切应力区域，使其易于产生斑块的脆性断裂.与S型支架相比，N型支架-血管耦合扩张构型在扩张段的低壁面切应力区域更小且壁面峰值切应力更低，从而降低了血管再狭窄和斑块破裂的概率.

(3) 在血管支架联接筋附近出现了较高的血管壁面等效应力区域，使其易于出现斑块的脆性断裂.与S型支架相比，N型支架-血管耦合扩张构型的血管壁面峰值等效应力更小，从而降低了斑块断裂的可能性.