预测倾斜气井临界携液流量新模型
2019-07-02杜社教梁钰王武杰仇栋杰
杜社教 梁钰 王武杰 仇栋杰
1.西安石油大学石油工程学院 2.上海理工大学能源与动力工程学院 3.陕西延长石油(集团)有限责任公司延长气田采气二厂
积液是气井生产过程中普遍存在的问题。随着气井不断开发,井筒携液能力随之下降,直至井内产出水不足以被气流连续携带出井外,最终在井底累积形成积液[1-4],对井底产生回压,抑制气井产量甚至造成停产[5-6]。因此,有必要对气井的临界携液流量进行预测和分析,从而采取合理的措施保障气井安全、高效地开发生产。
国内外许多学者都提出了气井临界携液流量的预测模型。其中Turner等[7]将直井作为研究对象,假设在高速气流的携带下液滴为球形,但预测结果偏高。李闽等[8]则认为液滴为椭球形,并在Turner模型的基础上进行修正。王志彬等[9]基于椭球形液滴假设,建立了考虑液滴形变影响的气井临界携液流量预测模型,但研究对象依然为直井。在考虑井斜角度的影响后,Belfroid等[10]在Turner模型的基础上进行角度修正,而杨文明等[11]则将倾斜气井作为研究对象,分析液滴在斜井中的受力情况,却忽略了气流携带液滴过程中液滴尺寸与形状的变化。所以,有必要建立考虑液滴形变与井斜角度影响的倾斜气井临界携液流量预测新模型,较为准确地预测倾斜气井临界携液流量,有效指导气井安全、合理的开发生产。
1 模型建立
只有当气井中最大直径液滴被气体携带出井外时,气井才能实现连续排液。将井内单个液滴做为研究对象,作出以下假设:①忽略液滴间的挤压、碰撞;②液滴为椭球形,水平截面为圆形,竖直截面为椭圆形,如图1所示;③液滴受气流影响发生形变时以中轴面为对称面,对称变形。
1.1 建立数学模型
液滴在倾斜气井中的受力情况如图2所示。液滴主要受到浮力、重力和曳力3个力的影响。当处于临界状态时,液滴沿气体流动方向所受合力为0,此时牛顿第二定律可以表示为:
R+Frsinθ-FGsinθ=0
(1)
式中:R表示曳力,N;Fr表示浮力,N;FG表示重力,N。
定义液滴变形参数k为液滴迎风面直径与液滴未变形前直径之比,即:
(2)
式中:d为液滴迎风面直径,m;d0为液滴未变形前球形直径,m。
则曳力R、浮力Fr和重力FG分别表示为:
(3)
(4)
(5)
式中:CD表示曳力系数;ρg表示气体密度,kg/m3;vc表示临界携液流速,m/s;g表示重力加速度常数;ρl表示液体密度,kg/m3。
当气井中最大直径液滴被排出井外时才能保证气井连续携液且不产生积液。而气井中最大液滴直径与临界韦伯数有关。因此,可以根据韦伯数定义得到气井中最大液滴直径为:
(6)
式中:σ表示气液间界面张力,N/m;Wecrit表示临界韦伯数。
将式(2)~式(6)代入式(1)中,得到气井临界携液速度为:
(7)
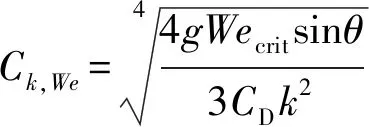
(8)
系数Ck,we表征了临界韦伯数、倾斜角度、液滴变形参数以及曳力系数对气井临界携液流速的影响。
气井临界携液流量为:
(9)
式中:qc为临界携液流量,m3/d;p表示压力,MPa;Z表示气体压缩系数;T表示热力学温度,K。
将推导所得的气体临界携液流速公式(7)带入式(9)中,即可得到相应的气体临界携液流量。
1.2 推导液滴变形参数
液滴被携带过程中受气流影响由球形变为椭球形。在这个过程中,液滴表面积增加,内能减少,忽略液滴间的传热和传质,根据能量守恒方程可得:
ΔE+ΔW=0
(10)
式中:ΔE为内能变化量,J;ΔW为液滴形变对外所做的功,J。
其中,内能变化量表示为:
ΔE=σ(A-A0)
(11)
式中:A为椭球形液滴表面积,m2;A0为球形液滴表面积,m2。
王志彬等[9]和熊钰等[12]根据式(11)计算椭球形表面积,但计算结果不够精确。
(12)
式中:h表示为椭球体高度,m。
本文采用纪兵等[13]推导得出的计算精度更高且形式简单的椭球表面积公式进行计算。
b2)c2-38656a6b6(3a4+2a2b2+3b4)c4+
10704a4b4(5a6+3a4b2+3a2b4+5b6)c6-
460a2b2(35a8+20a6b2+18a4b4+20a2b6+
35b8)c8+35(a2+b2)(63a8-28a6b2+58a4b4-
28a2b6+63b8)c10)π)
(13)
式中:a、b、c分别为椭球形3个半轴长度,m。a、b为椭球迎风面半径,c为椭球形液滴高度的1/2。
液滴在携带过程中,迎风面与背风面各点所受压力不同,所以需要对液滴表面进行积分才能得到液滴变形对外做的功,即:
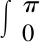
(14)
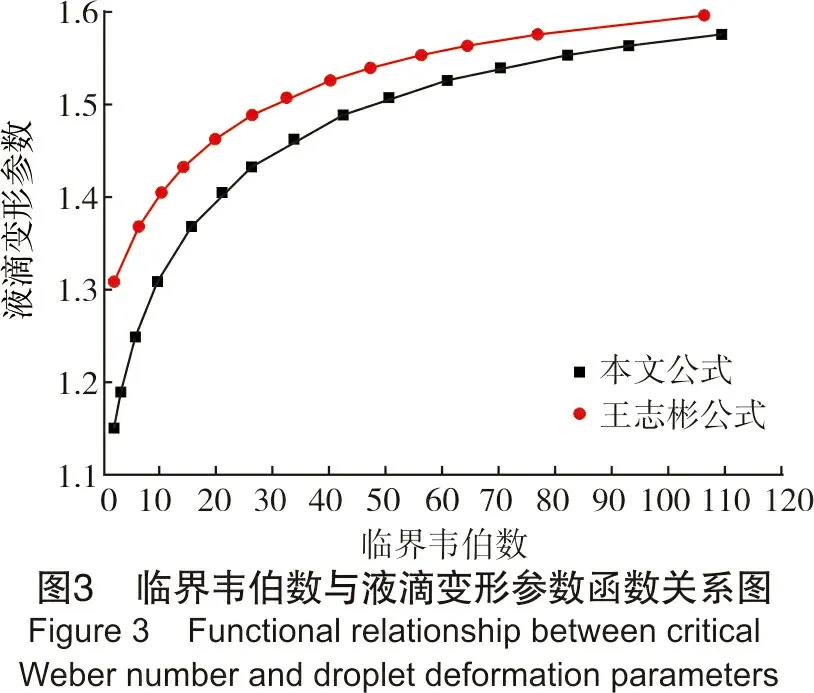
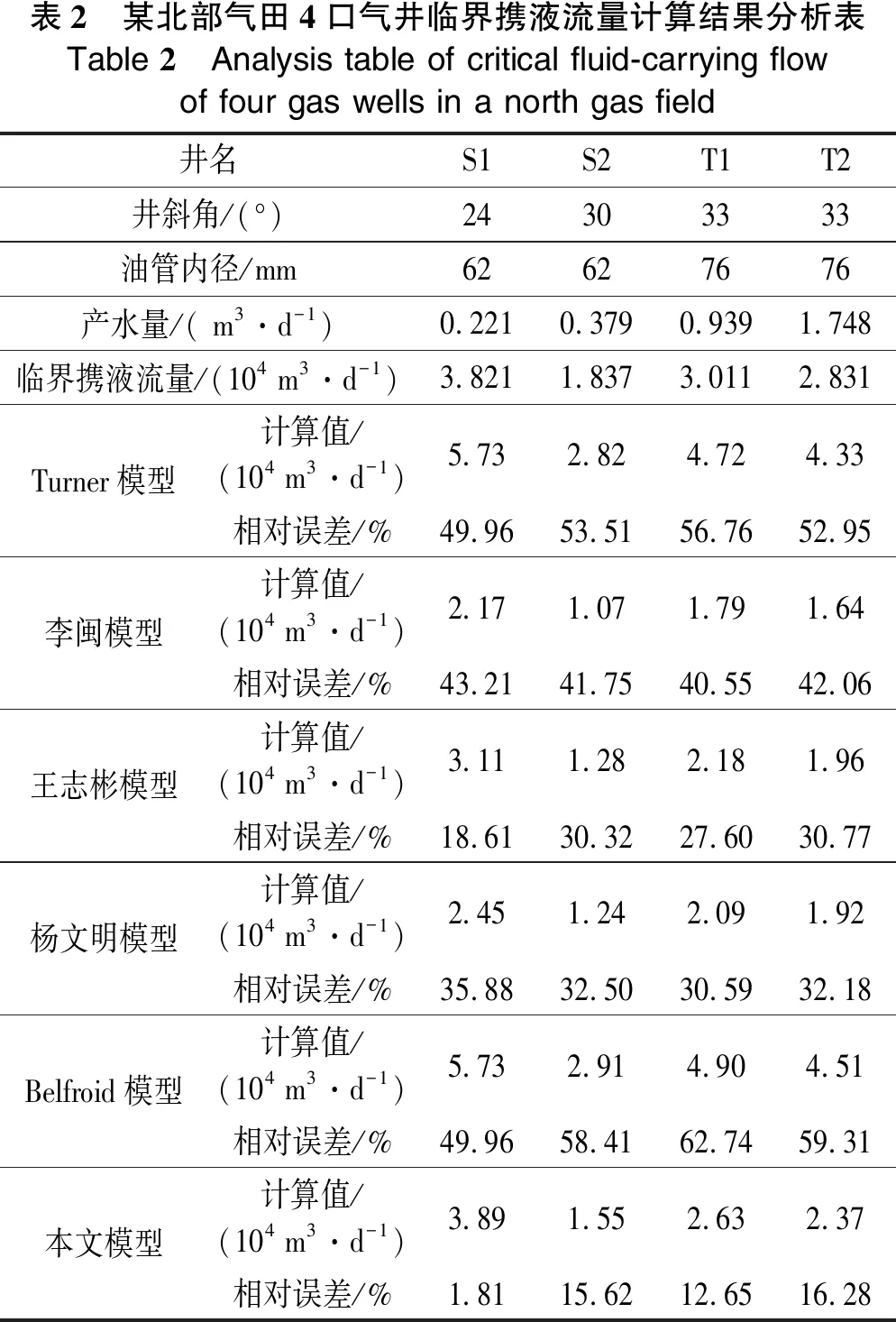
当1000 (15) (16) 根据液滴变形前后体积不变,可以得到椭球体液滴高度,从而得到液滴微元面径向位移为: (17) (18) 利用麦夸特法及通用全局优化算法对式(18)进行非线性拟合得到: f(θ,k)=0.862+0.083k-1.442θ+2.704θ2- 1.939θ3+0.518θ4 (19) 将式(15)、式(16)、式(17)和式(19)带入式(14)积分可以得到式(20)。 联立式(10)、式(11)、式(13)和式(20),可得到临界韦伯数与液滴变形参数的函数关系式(21)。 (20) (21) 将本文临界韦伯数与液滴变形参数的函数关系式与王志彬[9]的函数关系式做对比,如图3所示。可以看出,二者大致趋势相符。当临界韦伯数Wecrit=1时,两者相对误差最大为11.42%。且根据Wierzba[15]的实验观测,当临界韦伯数Wecrit=11时,液滴的变形参数k=1.32,王志彬[9]的函数关系式计算结果为k=1.41,相对误差为6.8%,而根据本文函数关系式计算得到k=1.33,相对误差为0.76%。由此看出,本文推导得到临界韦伯数与液滴变形参数的函数关系式较为可靠。 考虑液滴形变及内部流动情况,液滴的曳力系数会随气体流速、压力变化,所以将Brauer模型[16]、Clift&Gauvin模型[17]、邵明望模型[18]以及GP模型[19]等几个常见的通过拟合经验关联式得到的曳力系数计算模型与引用较为广泛的曳力系数实验值对比[20]。从而得到以上模型与实验数据的对比图,如图4所示。通过计算Brauer模型的平均误差为9.18%,Clift&Gauvin模型为19.49%,邵明望模型为2.07%,GP模型为2.71%。 从图4可看出:Clift&Gauvin模型计算结果偏低;Brauer模型与实验值偏差较大;GP模型在Re<20 000时,计算结果比较准确,但当Re>20 000时,计算结果偏低;邵明望模型的计算结果相对接近实验值。所以,最终选用邵明望模型计算液滴的曳力系数。 因为以上模型均是基于液滴为刚性球体下得到的曳力系数计算值,而本文研究对象为椭球形液滴,所以曳力系数会与以上模型计算结果存在偏差。Liu等[21]认为扁平体的曳力系数是圆球体的3.632倍,而椭球体介于扁平体与圆球体之间。Helenbrook等[22]认为,因为受到内部流动影响,液滴与相同尺寸的刚性球体相比,曳力系数偏小。 综合考虑液滴变形及其内部流动情况并参考王志彬模型[9]之后,基于邵明望模型[18],将计算结果降低15%作为椭球形液滴的曳力系数,表达式如式(22)。 (22) 为求解气井临界携液流速,还需通过计算得到液滴的临界韦伯数及气液界面张力。临界韦伯数随液滴直径变化而不同,Turner[7]、杨文明[11]等为了便于计算,取临界韦伯数为定值,在考虑气体流速对液滴形状的影响之后,本文采用Azzopardi[23]提出的计算公式来计算液滴临界韦伯数以提高模型精度。 表1 倾斜气井临界携液流量计算结果对比表Table 1 Comparison of critical fluid-carrying flow calculations for inclined gas wells井名ABCX168-1CX489-1CX493DCX616-1MP42-3MP52DT-Q123S4X3井斜角/(°)88.989.243332635372730003033压力/MPa8.027.282.591.818.3018.001.736.7015.507.208.286.8018.10产水量/( m3·d-1)0.017.130.600.030.600.110.180.205.500.020 20.178 173.908.00产气量/(104 m3·d-1)3.010.571.030.515.302.050.884.142.740.607 25.341.923.13临界携液量/(104 m3·d-1)计算结果Turner模型计算值3.735.353.291.833.795.371.793.447.185.185.554.958.04李闽模型计算值1.412.031.250.691.442.030.681.302.721.962.101.883.05王志彬模型计算值2.183.131.680.892.233.420.871.974.402.943.213.125.21杨文明模型计算值4.605.961.640.741.792.550.731.632.762.362.522.333.82Belfroid模型计算值1.151.463.722.084.195.962.043.836.144.304.605.558.92本文液滴模型计算值0.831.091.931.062.784.201.012.445.513.794.153.926.47气井状态未积液积液积液积液未积液积液积液未积液积液积液未积液积液积液 (23) (24) (25) 式中:Gle为液滴质量流量通量,kg/(m2·s);Wel表示液相临界韦伯数。 因为液滴界面张力是随压力、温度变化而变化的。为了提高模型准确性,本文选用李元生[24]根据分段拟合得到的密度差大于0.4 g/cm3时的气水界面张力经验关系式来计算液滴的界面张力,关系式如式(27)。 (26) 式中:σgw为气水界面张力,mN/m;Tr为拟对比温度。 将式(21)、式(22)、式(23)和式(26)带入式(7)中,即可得到倾斜井筒内临界携液流速。 采用渤海A气田、川西气田及塔里木油田等共13口定向气井对本文模型进行分析[11,25-28]。通过计算得到几种常用模型及本文模型的临界携液流量,其中红色表示气井积液情况预测错误,黑色表示积液情况预测正确,具体如表1所列。 对某北部气田4口气井临近积液时的携液流量进行分析[29],详情见表2。 表2 某北部气田4口气井临界携液流量计算结果分析表Table 2 Analysis table of critical fluid-carrying flow of four gas wells in a north gas field井名S1S2T1T2井斜角/(°)24303333油管内径/mm62627676产水量/( m3·d-1)0.2210.3790.9391.748临界携液流量/(104 m3·d-1)3.8211.8373.0112.831Turner模型计算值/(104 m3·d-1)5.732.824.724.33相对误差/%49.9653.5156.7652.95李闽模型计算值/(104 m3·d-1)2.171.071.791.64相对误差/%43.2141.7540.5542.06王志彬模型计算值/(104 m3·d-1)3.111.282.181.96相对误差/%18.6130.3227.6030.77杨文明模型计算值/(104 m3·d-1)2.451.242.091.92相对误差/%35.8832.5030.5932.18Belfroid模型计算值/(104 m3·d-1)5.732.914.904.51相对误差/%49.9658.4162.7459.31本文模型计算值/(104 m3·d-1)3.891.552.632.37相对误差/%1.8115.6212.6516.28 通过分析可看出,Turner模型[7]、李闽模型[8]、王志彬模型[9]的计算结果偏差较大,甚至出现了误判的情况,用这4个以直井为研究对象的计算模型来预测倾斜气井的临界携液流量显然不够准确。对比杨文明模型[11]、Belfroid模型[10]以及本文模型,发现本文模型的计算结果更精确,并且全部正确判断出气井的积液情况,与现场实际情况吻合,侧面说明了本文模型的准确性与可靠性。 (1)基于王志彬模型,引入更为精确的椭球表面积计算公式,通过能量守恒方程得到新的液滴变形参数与临界韦伯数函数关系式,提高了模型的准确性。 (2)液滴曳力系数会因为受到气体流速与压力的影响而发生变化。通过4种曳力系数计算模型对比,最终选择基于邵明望模型将计算结果降低15%作为椭球形液滴的曳力系数以提高模型精度。 (3)相比于其他临界携液流量模型,本文模型与现场实际情况吻合程度更高,计算精度提高14.49%~16.80%,能比较准确地预测出倾斜气井临界携液流量,有效指导倾斜气井的生产。
1.3 计算曳力系数

1.4 临界韦伯数与气液界面张力

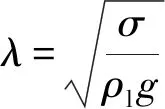
2 实例验证
3 结论
