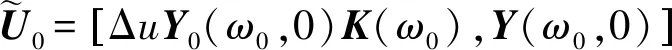On Coordination Control of A Class of DEDS
2019-07-02ZhangWengangLiChuntao
Zhang Wengang Li Chuntao
(Basic Science Department, Wuchang Shouyi University,Wuhan 430064, Hubei)
[Abstract]In this paper, the problem of coordination control for a class of DEDS with flow-shop structure was discussed by the method of Cohen’s max-algebra. The non-blocking uniform time control conditions of system without buffer were discussed. It is proved that the necessary and sufficient conditions for the non-blocking uniform time control without buffer are feedback on linear state. The important parameters of system can be expressed directly through the processing time matrix of the system; meanwhile, the complexity of computation caused by too large matrix dimension is avoided.
[Key words]DEDS; max-algebra; eigenvalue; blocking; coordination control
1 Introduction
The terminologies and symbols in references [1~5] and the relevant conclusions in references [2~4] without proclaiming were used in this paper. It is well-known that the serial production streamlines which havem×n-flow-shop structure with allocated buffer, are an important class of DEDS. Generally, Cohen’s max-algebra method is adopted to research the optimal control and scheduling problems. The matrix analysis method was used in both reference [2,3] , but it made much difficulty to practical computation due to the larger dimensions of matrix; In references[4,5] , the arrays iteration was applied to generalize the related results of the case of containing finite buffer; the method proposed in references [4,5] was continuously used to research the flow-shop on the changing order set, and the relevant results in references [4,5] were improved.
Having flow-shop structure system with buffers is an important class of DEDS. It could be seen as the plane lattice, which uses max-algebra to operate networks as basic models. The controlled objects and mathematical models in this paper are analogues to those in references [2~5] , which satisfy the conditions as follows.
1)n-JobsJ1,J2,…,Jnprocess onm-machinesM1,M2,…,Mm, with the processing time matrix [tij]m×nas a given constant matrix;
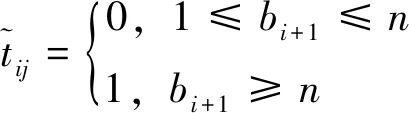
3)tijrepresents processing time when jobJjprocesses on machineMi,ω0=(1,2,…,n)is a processing order set of the jobs,T(ω0)=[tij]m×ndenotes processing time matrix.

Then the max-algebra expression of (i,j) module is as below:
(1)
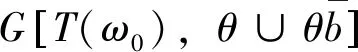
X=[x11,…,x1n,x21,…,x2n,…,xm1,…,xmn]
Equation (1) is rewritten to dynamic programming simultaneous equations as follows:
(2)
where 1≤bi+1 To process itemxi+1,j-bi+1appropriately, we can set state Cohen equation of stateXin the following equation: (3) Y(k)=[x1n(k),x2n(k),…,xmn(k)] then we have: (4) whereki,0denotes converting time when two sets of job adjacent are processed;Kmis called machine feedback matrix. When we define sample matrixCwhich satisfiesY(k) =X(k)C, block matricesA,Bsatisfy the following equation: (5) According to (3) ~ (5), we can obtain the output equation with control itemU(k) as follows: (6) whereA∈Dm×m,B∈Dn×m, andDis max-algebra. The state equation (3) is rewritten to the following form: (7) wherei=1, 2,…,m;j=1, 2,…,n. The definitions of machine free time and job waiting time are introduced as below: (8) whereIW0j=IWi0=0,i=1,2…,m;j=1,2,…,n. System (8) represents the time when jobJjhas been processed on machineMi; jobJj-bi+1has been processed on machineMi+1leading toJ’js being blocked byBi+1on a capacity unitMi. Setting: (9) wherei=0,1, 2,…,m;j=1, 2, …,n. Equation (9) represents the time when jobJjhas been processed on machineMi, jobJj-1has not been processed onMi+1, leading toJj’s getting into non-machine buffer for wasting blocking. Letting: (10) wherei=0,1, 2, …,m;j=0,1,2, …,n-1. Equation (10) represents the time when jobJjis released from machineMi, but jobJj+1is not released fromMi-1. (11) (12) ⟺∀i,j,xij=cij>ci+1,j-1 (13) For the given system processing time matrixT(ω0)=[tij]m×n(tij>0),we useU*to indicate (n+m)-dimensional vector set of resource input [x01,…,x0n,x10,…,xm0]which satisfies condition (13).SX(ω0) = [T(ω0),b,U,A,B] is used to represent the open-loop system,representing closed-loop output system with control item derived bySX(ω0) . (14) The intensive proof of Th. 2 see Th. 3 in reference [5]. The conclusions can be summarized from the results above and foregoing as below: 2) WhenSX(ω0) and 0SY(ω0) take the same machine inputY(k-1): (15)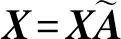
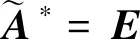

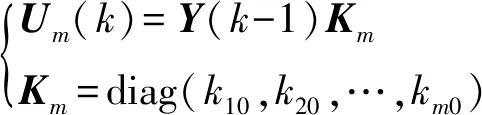

2 Basic Principles and Theorems

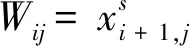
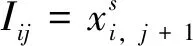
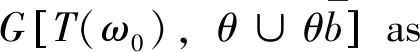
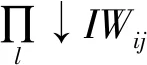
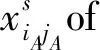

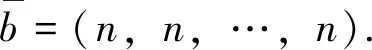
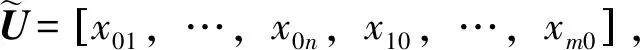

3 Major Results


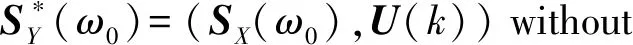
4 Conlusion