聚焦问题“题眼” 调控解题方向—— 以一道椭圆三角形面积问题的解题研究为例

吴燕梅

(江苏省海门中学 226100)

在平时的高中数学教与学中，我们不可避免会引导学生对数学问题进行一系列研究，每个问题都有其考查的意图.如果抓住问题的要害，即“题眼”，顺藤摸瓜，进而对解题方向给出合适的调控，不仅会收获各种解法，同时会建立不同的思维方式，提升学生围绕题的本质去探究解题的能力.本文以一道解析几何问题为例，抛砖引玉.

一、问题呈现

一种画椭圆的工具如图1所示．O是滑槽AB的中点，短杆ON可绕O转动，长杆MN通过N处铰链与ON连接，MN上的栓子D可沿滑槽AB滑动，且DN=ON=1，MN=3．当栓子D在滑槽AB内作往复运动时，带动N绕O转动，M处的笔尖画出的椭圆记为C．以O为原点，AB所在的直线为x轴建立如图2所示的平面直角坐标系．

(1)求椭圆C的方程；

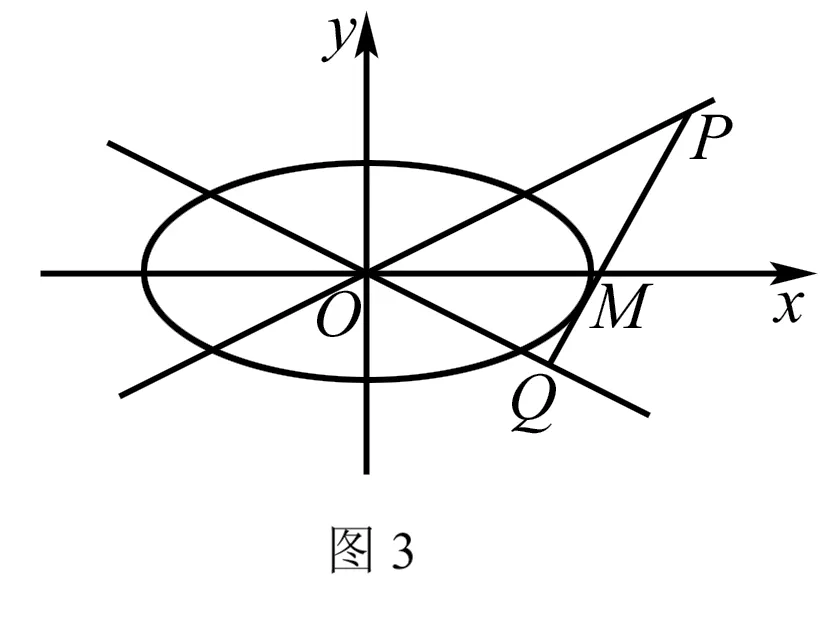
(2)设动直线l与两定直线l1:x-2y=0和l2:x+2y=0分别交于P，Q两点．若直线l总与椭圆C有且只有一个公共点，试探究：△OPQ的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．

二、问题分析

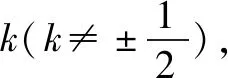
因为直线l与椭圆相切，联立方程：

不妨记点P(x1,y1),Q(x2,y2)，

当k=0时，S△POQ=8；

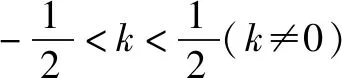
综上，S△POQ面积最小值为8．

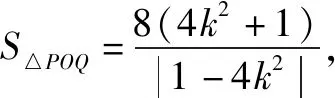
思路2面积割补法

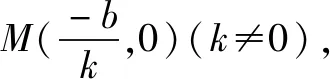
当k=0时，S△POQ=8，故S△POQ面积最小值为8．

点评图形面积(尤其是不规则图形)通过分割法转化为有特殊关系的图形面积之和，可以简化计算；这题当中随直线变化，交点P,Q可能位于x轴同侧，所以S△POQ=|S△POM-S△QOM|，结果同法2分析．

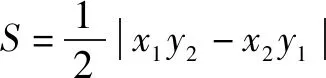
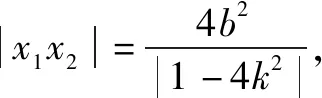
点评这题解法思路，学生是通过平时作业或练习中处理过类似的面积问题，通过联想迁移，进而构建固定的数学模型，为简化化简工作提供了很好的思路．(下面是前期练习中出现的问题(1)，证明可以独立尝试多种解法．)

联想已知椭圆x2+2y2=1，过原点的两条直线l1和l2分别与椭圆交于A,B和C,D，设△AOC的面积为S．

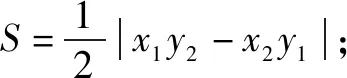
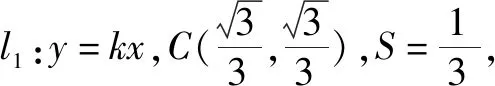
(3)设l1与l2的斜率之积为m，求m的值，使得无论l1与l2如何变动，面积S保持不变．

思路4巧用椭圆切线方程，调控切线表示．

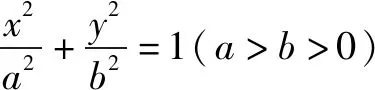
思路5发现定值关系，调控最值计算．

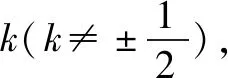
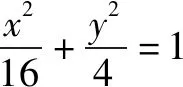
点评解析几何中涉及最值问题，往往会结合题中条件找到定量关系(定值)，从而为利用基本不等式研究最值创造条件，本题这种解法学生也容易在平时解决的问题中类比联想找到.