小圆用处大

吴芳蓉

(福建省龙岩市龙岩初级中学 364000)

本文以构造辅助圆解决问题为例，阐述如何通过挖掘题目中的隐含条件，抽出能构造辅助圆的相关基本模型，巧妙地构造出符合题意特征的辅助圆，使问题中复杂的关系和性质在新构造的图形中清晰地展现出来，达到化隐为显，化繁为简的解题功效.

一、根据有关线段相等构造辅助圆(等距离型)

人教版九年级上第24.1 对圆的定义为：圆上各点到定点的距离都等于定长；到定点的距离等于定长的点都在同一个圆上.

例1(2018宁德质检改编)如图1，已知等腰△ABC，AB=BC，D是AC上一点，线段BE与BA关于直线BD对称，射线CE交射线BD于点F，连接AE，AF，若∠ABC=α，则∠AEF=____.(用α的代数形式表示)

分析由AB=BC及线段BE与BA关于直线BD对称，可得BA=BC=BE，即可构造出以B为圆心，BA长为半径的圆，此时A、C、E均在⊙B上，如图，构建⊙B的内接四边形AGCE，则可把∠AEF转化为四边形AGCE的外角，利用“圆的内接四边形的一个外角等于其内对角”，把问题转化到求圆周角∠AGC.

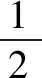
例2在平面直角坐标系中，O为坐标原点，已知A(1，1)，在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数为____．

分析因△AOP是等腰三角形，则有两条同顶点的线段相等，即可构造以等腰三角形顶角的顶点为圆心，腰为半径的辅助圆.

解如图2，若△AOP为等腰三角形，则

(1)若AO为腰时，有两种情况:

①当AO=AP时，点P是以A为圆心，AO为半径的圆与x轴的交点，此时⊙A与x轴有1个交点P1；

②当OA=OP时，点P是以O为圆心，OA为半径的圆与x轴的交点，此时⊙O与x轴有2个交点，分别为P2、P3；

(2)若OA为底时，P是OA的中垂线与x轴的交点，有1个交点，为P4．

以上4个交点没有重合的．故符合条件的点有4个．故填：4.

方法总结：在某些几何问题中，当出现几条共同顶点的线段相等时，可利用圆的定义，构造出一个辅助圆，利用圆的有关性质，使问题得以解决，可把这种情形称为等距离型.

等距离型的基本图形为：如图3，若AB=AC=AD，则B、C、D在以A为圆心，AB长为半径的圆上.

二、根据定张角构造辅助圆(定张角型)

例3如图4，B是线段AC的中点，过点C的直线l与AC成60°的角，在直线l上取一点P，使得∠APB=30°，则满足条件的点P的个数是( ).

A.3个 B.2个

C.1个 D.不存在

分析由∠APB是一定角(数量相等，点P位置不固定)，AB是一定长，可构造出辅助圆，此圆以AB为弦，圆心角∠AOB=60°，得出P点是优弧AB上的点，进而把问题转化到圆与直线的位置关系的问题.

解如图4，作等边△OAB，以O为圆心，OA长为半径作圆，作BM⊥l于M，OH⊥l于H，

∵B是AC的中点，∴令BC=AB=m.

∴OB>OH，∴直线l与⊙O相交，∴点P的个数是2个.故选B.

我们可把有这种关系的图形称为定张角、定线段型，其基本图形为：如图5，若AB是一定值，∠C的度数是一定值，但点C是动点，则可把∠C转化为过AB两点的圆的圆周角(∠O=2∠C).

三、根据直角构造圆(直角型)

直角型所用的圆的性质为：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径，有这种关系的可称为直角型.

直角型的基本图形为：如图6，若∠C=90°，则点A、B、C在以AB为直径的圆上.

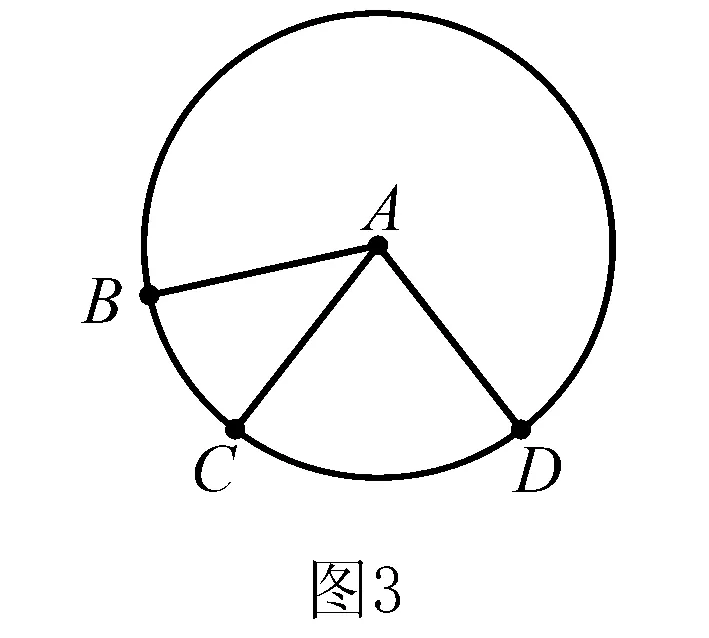
例4(2016年安徽省中考)如图7，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为( ).

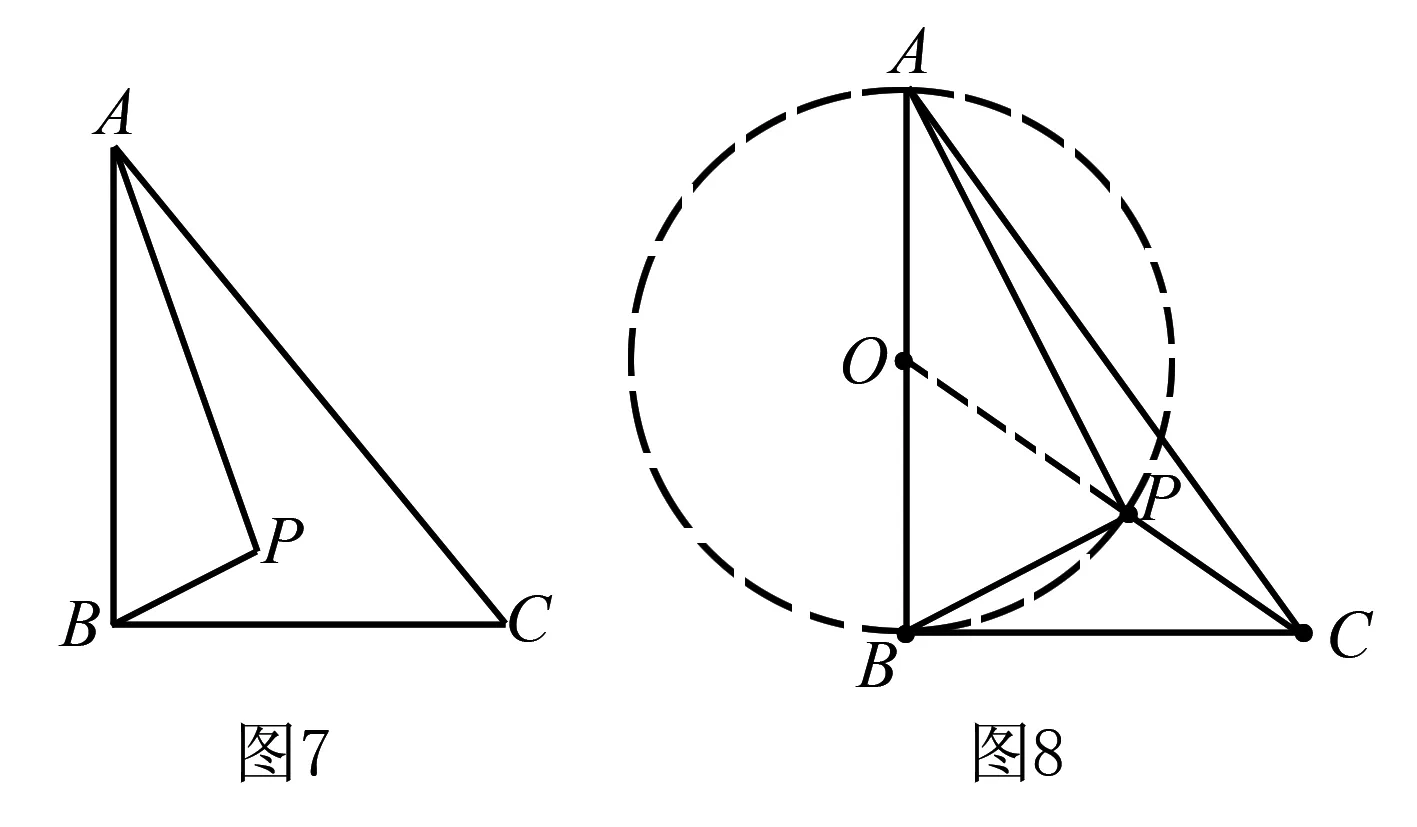
分析在此题中，先分析出∠APB=90)，则点P在以AB为直径的⊙O上，如图8，连接OC与⊙O交于点P，此时PC最小.

总之，构造辅助圆解决问题的关键是要善于发现隐含于题目中与圆的有关信息，抓题目的特征，抽取出构造圆的基本图形，巧作一圆，把圆用“活”，实现小圆大用处.