问题解得清如许 为有源头析得深

金玲玲

(浙江省台州中学 318000)

一、 提出问题，穿针引线

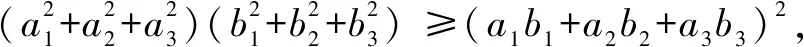
生：已知a2+b2+c2=1,求a+b+c的最大值.(解略)

笔者认为让学生自己出题可大大提高学生的学习兴趣，也可进一步检验学生掌握知识的能力和水平.前苏联心理学家维果斯基认为，学生的思维发展水平可以区分为两种，一种是现有发展区，这是教学的出发点；第二种是最近发展区，它是一种潜在的、可能的发展水平，只有经过教师不断地启发指导和学生自己努力所能够达到的发展水平，这才是教学所应该努力追求的目标.本节课开门见山地提出课题的中心并要求学生自己出题，而恰恰这样的启发，让学生处于“跳一跳摘果子”的状态，不仅可以解决问题，而且又能激发学生的求知欲.

二、局部调整，深入探究

师：变式1.条件不变，求a+2b+3c的最大值.

变式2.条件不变，求a-2b+3c的最大值.

变式可以先在条件不变的情况下，改变另一些条件的形式，使问题进一步简单地深化.变式的目的使学生有机会亲历习题发生“化学变化”，进而理解其本质特征，进一步提高学生的创新能力和解决分析问题的能力.

师：你能将条件一般化吗？题目形式又会发生怎样的变化呢？

生：变式3.已知条件改为2a2+3b2+5c2=1，求a+b+c的最大值.

生：变式4.已知条件改为2(a-1)2+3(b-2)2+5(c-3)2=1，问题同上.

生：变式5.已知a+b+c=1,求a2+b2+c2的最小值.

生：变式6.变式5的条件不变，求a2+4b2+9c2的最小值.

生;变式8.求(a-1)2+4(b-2)2+9(c-3)2的最小值.

笔者以为以上选择的习题非常具有典型性.华罗庚先生曾经讲过，学习数学有两个过程，其一是由薄到厚，其二是由厚到薄.而在高三的复习过程中，我们需要选择后者.这势必要求我们充分发挥试题的教学功能，让变中出彩，让“源头”丰富起来，从而让习题“源远流长”.

三、更换条件，声东击西

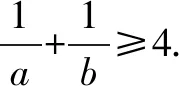
变式6 试改变条件，设计出其他的问题.

在中学数学习题变式教学中，对习题的变式要循序渐进，有的放矢.变式在于对某种方法的深刻认识和巩固.有位特级教师说过：“如果知识的背后没有方法，知识只能是一种沉重的负担；如果方法的背后没有思想，方法只不过是笨拙的工具.”就数学学习而言，学生的智慧集中体现在对数学思想方法的深刻领悟和自觉运用上，可以说领悟与运用数学思想方法的过程就是学生智慧生长的过程.所以，一堂课的题目不在于多，而在于精，要在选题上做到以少胜多.作为教师，我们更要教会学生顺藤摸瓜，扩大成果，做到举一反三，触类旁通.所以我上一系列变式设计目的在于，让学生对似曾相识的题目回顾，易联想到构造公式所需要的结构，从而灵活运用柯西不等式.而以上6点使用柯西不等式进行变式，一气呵成，思路自然，不偏不怪，又展示出试题”柔“的一面，贮存着丰富的内涵，又有良好的区分度.

四、改头换面，刚柔并济

在习题变式教学中，对习题的变式要注意纵向联系，让学生在学习新知识的同时对旧知识也得到复习，让学生明白“任何事物都是相互联系的”这一哲学道理.

师：我们可顺势延展到2009浙江高考03号题 已知正数x，y、z满足x+y+z=1.

(2)求4x+4y+4z的最小值.

五、教学反思

G·波利亚早就指出：“解题的价值不是答案的本身，而在于弄清‘是怎么样想到这个解法？’‘是什么促使你这样想，这样做的’.”这就是说，解题过程是一个思维过程，是一个把知识与问题联系起来思考、分析、探索的过程，是教师引导学生“用自己的头脑亲自获得知识的再发现过程”.本课的设计始终贯彻让学生认清柯西不等式的本质结构，积极引导让学生交流思考，构造不等式，由此，冰冷的知识被思维过程所点燃，思维的障碍经概念理解而飞跃，优美的解法被数学思想驾驭，知识的运用和知识的产生得以同步发展.