TBM刀盘分体结构参数化优化设计方法*

朱庆东

(鞍山师范学院 美术学院，辽宁 鞍山 114007)

0 引言

全断面岩石隧道掘进机(TBM)是一种大型地下岩石全尺寸钻孔设备，逐渐成为一种最主要的掘进工具[1]。TBM对不利的地质条件非常敏感，包括冲击、断裂、破裂、岩石破碎、挤压、膨胀和高进水量[2]，其稳定性直接影响工程效率。TBM刀盘分体位于刀盘边缘，其振动变形尤为剧烈，因此通过对刀盘分体的结构进行优化设计来减小振动变形对于TBM工作的稳定性尤为重要，具有重要的工程实用性和创新性。

目前国内外学者在TBM结构优化方面进行了大量的研究，Deng等[3]据非等距驱动系统的传力和变形特性，对推力系统进行了非均匀布置优化，使其在隧道施工中具有较高的控制精度，也能避免共振。Huo等[4-5]考虑了冲击载荷时变和刀具与夹持器靴的多组分复杂关系，建立了一种动态耦合非线性模型，并对圆柱铰链和电机与小齿轮之间的连接轴和大齿轮进行了优化设计。另外，Huo分析了TBM刀具的振动响应和载荷传递规律，提出了刀具结构优化方案。Ling等[6]通过建立TBM刀盘系统多自由度耦合动力学模型，对TBM刀盘重量等参数进行了优化设计，实现了刀盘轻量化处理。Gong等[7]针对TBM掘进时高地应力引起的隧道壁面失稳、高压地下水流入等问题，对修改机器和操作模式进行了改变，并对支撑参数进行了优化。凌静秀等[8]在已有TBM刀盘系统耦合动力学模型的基础上建立了适用于TBM刀盘强迫振动响应的灵敏度分析方法，并对分体质量占比进行了优化分析。彭欢等[9]为减弱基础振动对流体出口参数的影响，运用正交实验法对管道进行结构优化，从而在一定程度上抑制了因基础振动带来的流体波动。综上所述，对于TBM结构优化已经取得了一定的研究成果，但是对于刀盘分体结构优化研究较少，由于TBM的实际工作过程复杂多变，而刀盘分体位于刀盘边缘，其工作环境尤为恶劣，因此刀盘分体结构合理性往往直接影响刀盘的掘进稳定性，也影响掘进的效率，因此对刀盘分体的结构优化显然很必要。

本文针对以上问题，提出了一种分体结构参数化优化设计方法。建立了TBM刀盘系统耦合动力学模型，对模型求解得到各分体的各向振动响应,通过对4个分体的响应分析比较得到振动稳定性最差的分体结构，对其进行有限元分析，得到加载时分体相应的结构尺寸数据、总体变形数据；并进行Pearson相关分析提取主要影响参数，通过数值分析得到各主要参数的最优参数区间，为刀盘分体的结构设计和优化提供了有效的理论依据。

1 刀盘系统动力学模型建立

刀盘形式主要以分体式刀盘为主，其中以中方五分式刀盘最为常见，如图1a所示[10]。刀盘分体作为TBM刀盘最边缘位置其直接与岩石发生剧烈切割作用，分体位置如图1b所示。刀盘分体的振动变形是非常剧烈的，它的稳定性和可靠性直接影响刀盘的稳定性和掘进的效率，因此如何从结构设计本身进行优化设计显得尤为重要。

(a) 中方五分式刀盘 (b) 分体位置图 图1 中方五分式刀盘与分体位置图

1.1 中方五分式刀盘系统模型建立

本文以典型的中方五分式刀盘分体作为研究对象，由于刀盘各分体的结构形式相似且与刀盘中心体的耦合方式相同，(见图2)，为了寻找能够代表其它分体的一个，因此首先建立刀盘系统的耦合动力学模型求得各个分体在刀盘系统中的振动响应情况，进而找到4个分体中最薄弱的一个进行研究，分析刀盘分体结构尺寸对刀盘稳定性的影响。

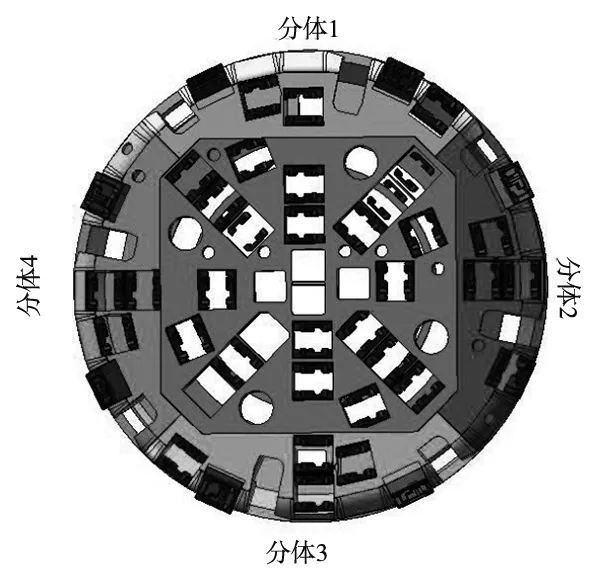
图2 刀盘分体位置图

将刀盘分体、刀盘中心体、大齿圈、驱动齿轮、盾体及小齿轮等效为质量点，其中，电机和减速器等效成一个质量点。通过分析各质量点在径向、轴向自由度的振动情况，利用集中质量法，分别推导出典型刀盘的等效力学模型。其中，x代表刀盘水平径向方向，y代表刀盘竖直径向方向，z为轴向(即TBM的掘进方向)。建立的中方五分式刀盘系统多自由度耦合力学模型如图3所示。

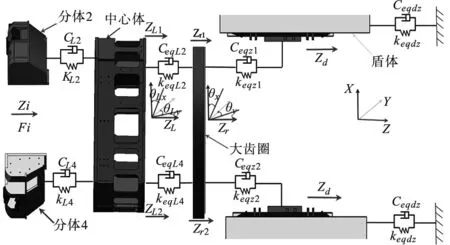
(a) 刀盘系统轴向等效力学模型

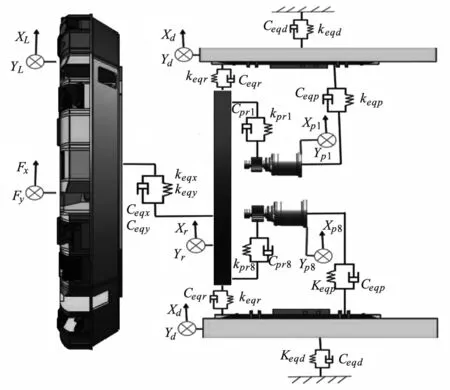
(b) 刀盘系统径向等效力学模型

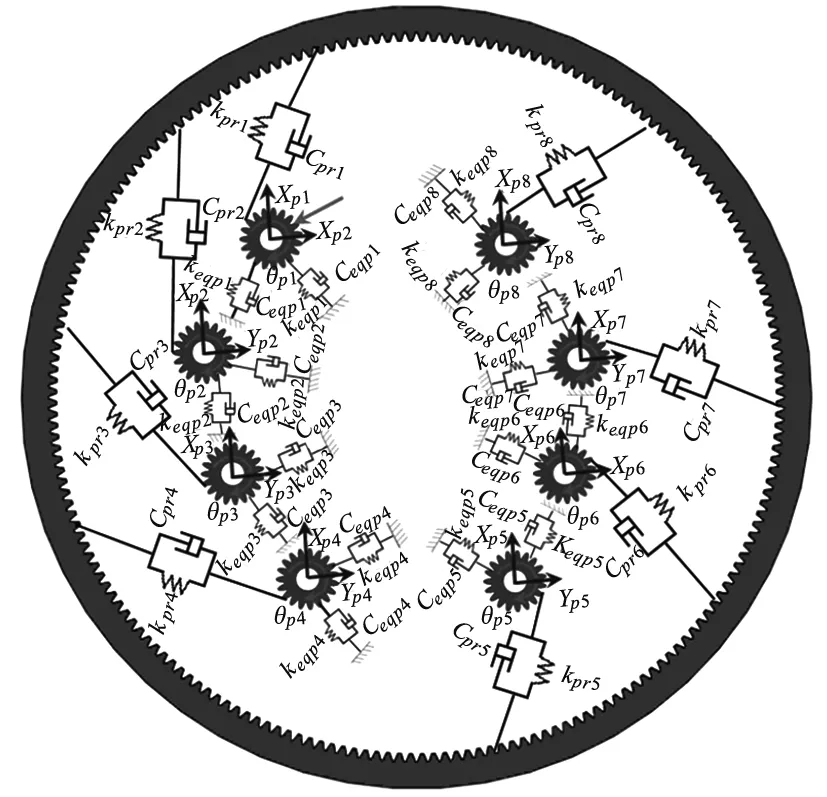
(c) 刀盘系统驱动齿轮啮合等效力学模型 图3 刀盘系统等效力学模型

mυ(υ=i,L,r,d,pj)分别代表刀盘各分体，刀盘中心块，大齿圈，盾体，小齿轮的等效质量；kι(ι=xi,yi,zi)—分别代表刀盘分体法向等效支撑刚度，切向等效支撑刚度及轴向等效支撑刚度；keqϑ(ϑ=x,y,L,r,z,d,dz,pj)—分别代表刀盘中心块横向、纵向、轴向等效支撑刚度，大齿圈径向、轴向等效支撑刚度，盾体的横向、纵向、轴向等效支撑刚度及小齿轮的等效支撑刚度；kmpQ分别代表小齿轮连接轴扭转刚度；Ceqϑ(ϑ=x,y,L,r,z,d,dz,pj)分别代表刀盘中心块横向、纵向阻尼系数，大齿圈径向、轴向阻尼系数及盾体的横向、纵向，轴向阻尼系数及小齿轮的阻尼系数；CmpQ分别代表小齿轮连接轴扭转阻尼系数；Fx,Fy,FL分别代表中心块横向、纵向载荷，刀盘轴向载荷；Fxi,Fyi,FLi分别代表刀盘分体法向、切向载荷以及刀盘分体轴向载荷；φLi为各分体初始相位角。

根据等效力学模型可知，刀盘系统的广义位移矩阵为：

{δ}>={xi,yi,zi,xL,yL,zL,xr,yr,zr,xd,yd,zd,Hpj,Vpj}T
(i=1～4，j=1～小齿轮个数)

(1)

矩阵中，xi,yi,zi分别表示刀盘各分体法向、切向、轴向位移；xL,yL,zL分别表示刀盘中心块横向、纵向、轴向位移；xr,yr,zr分别表示大齿圈横向、纵向、轴向位移，倾覆振动位移及扭转振动位移；xd,yd,zd分别表示盾体横向、纵向、轴向位移；Hpj,Vpj分别代表各小齿轮切向、径向位移。

1.2 动力学微分方程的建立

根据建立的等效力学模型，根据牛顿第二定律，综合考虑各构件上载荷平衡关系，推导出刀盘、大齿圈、盾体、小齿轮的微分方程，然后联立得到刀盘系统的多自由度微分方程组如下所示。

(1)刀盘

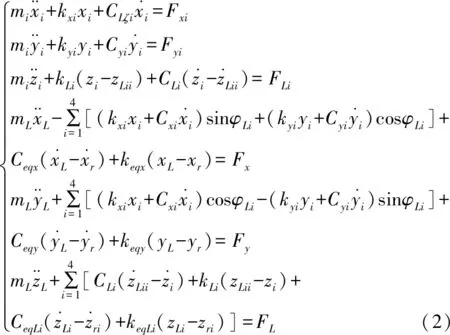
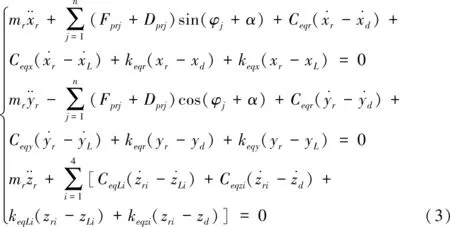
(3)盾体

采用origin8.0绘图，采用SPSS20.0对数据进行相关性分析、显著性检验，所得结果用平均值±标准差（±sd）表示，以 p＜0.05作为差异显著性检验标准。

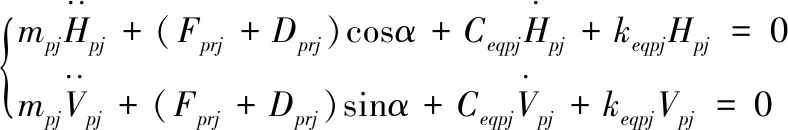
(5)

上式中，ZLii,ZLi和Zri分别指刀盘分体轴向振动位移和刀盘中心块倾覆摆动角度之间的相互关系，刀盘中心块的轴向位移和倾覆摆动角度之间的关系，大齿圈的轴向振动位移和大齿圈的倾覆摆动角度的相互关系。其中aL为刀盘中心块边长的一半，rb为大齿圈基圆半径。

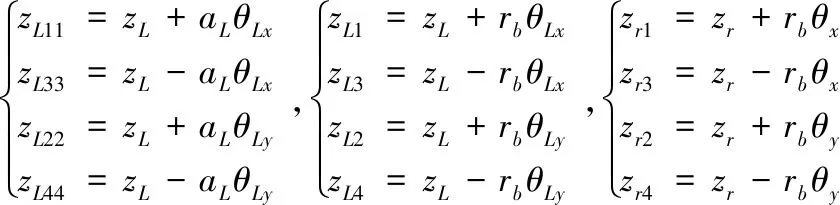
(6)

2 动力学结果分析及刀盘结构优化参数的提取

2.1 动力学结果分析

通过对已建好的动力学微分方程进行求解可得到，在考虑到分体在刀盘系统中的耦合时，4个分体轴向、径向和法向的动力学响应，如图4所示。

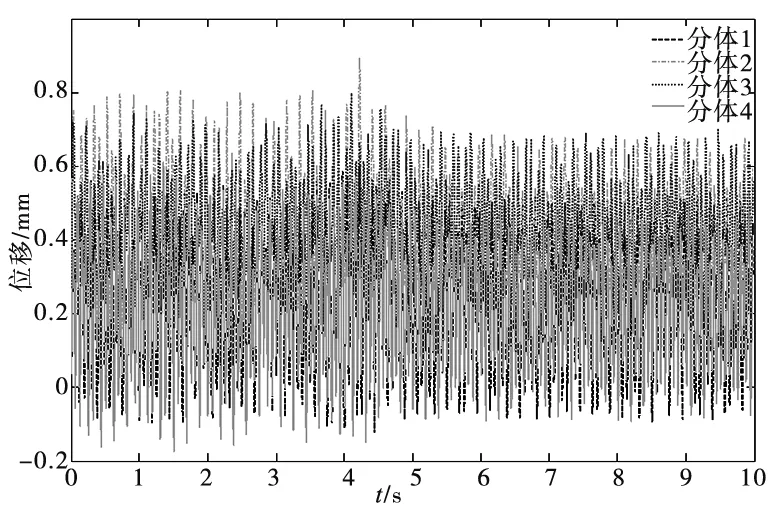
(a) 分体轴向振动位移

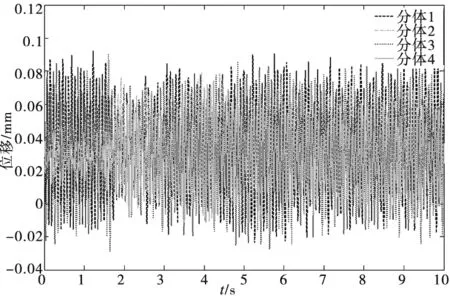
(b) 分体切向振动位移

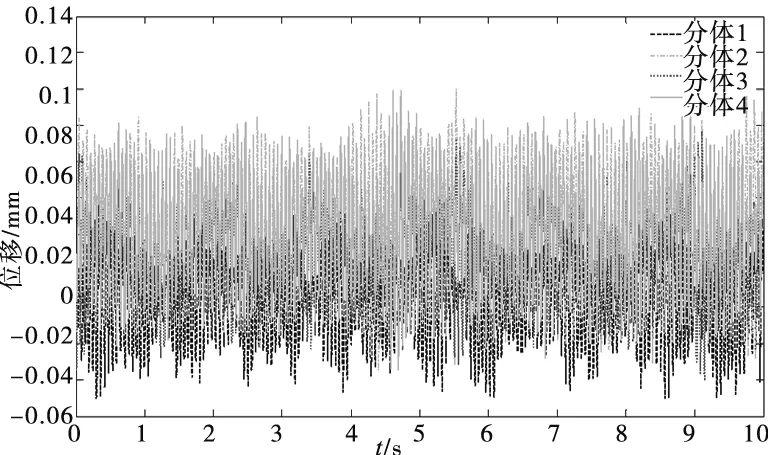
(c) 分体法向振动位移 图4 分体振动位移响应

由图4可见，刀盘各分体三个平移方向的振动形式均表现较大的随机性，也说明了对其进行结构优化的必要性；刀盘各分体切向振动幅度不超过0.1mm，刀盘各分体法向振动幅度不超过0.14mm；轴向振动幅度较大，最大振动幅度约1.2mm，分体切向振动幅度是其振动幅度的8.4%，分体法向振动幅度是其振动幅度的11.7%，由此可见轴向振动变形相对切向和法向要大的多，且分体2的振动较其它三个分体要大，因此本文选取分体2轴向振动作为结构优化对象。

2.2 结构优化参数的提取

由于本文是通过有限元分析参数化的结构尺寸来分析刀盘最后设计尺寸，因此需要选取刀盘结构尺寸作为变量尺寸，选取的刀盘分体2的结构尺寸参数如图5所示。

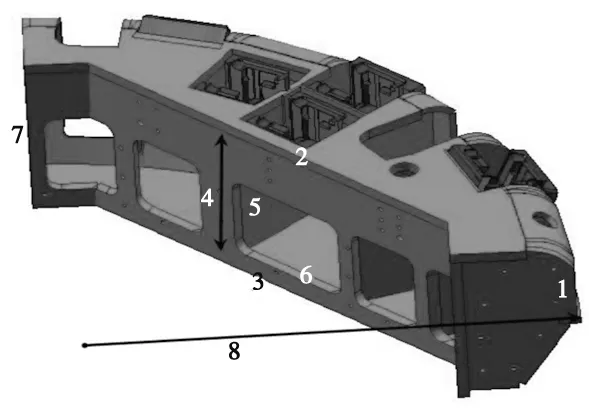
1.分体弧板厚度 2.前面板厚度 3.后面板厚度 4.前后面板间距 5.筋板厚度 6.连接板厚度 7.边板厚度 8.外弧半径

图5 结构优化参数

3 有限元分析和有限元结果的参数化

3.1 有限元分析

为了完全仿真分体在刀盘上的实际情况，将分体优化尺寸选取后，对整个刀盘的变形作为分析结果，来达到结构尺寸全局优化的目的。刀盘进行网格划分如图6a所示，共有1049694个节点和534242个单元。另外，载荷的添加如图6b所示。

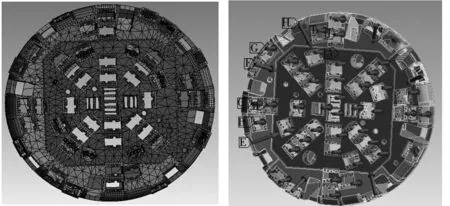
(a) 网格划分图 (b) 载荷添加图 图6 网格划分及载荷添加图

3.2 有限元分析结果参数化

根据轴向力进行分体轴向施力，并将后面板作为固定约束进行仿真分析，并利用超拉丁方采样对仿真结果进行采样，最终可得加载时分体相应的结构尺寸数据和总体变形数据，共1268组，部分采样数据如表1所示。

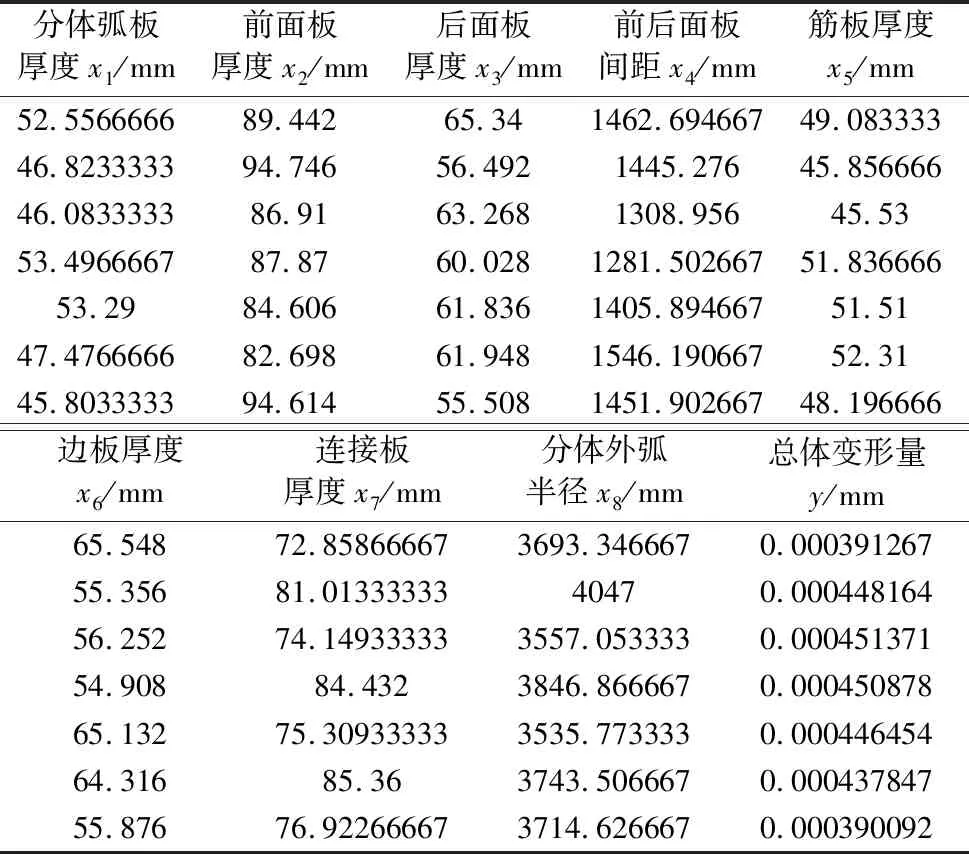
表1 部分采样数据

4 Pearson相关性分析及优化尺寸区间的确定

4.1 Pearson相关性分析

相关性分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析[11]。用 Pearson相关系数来描述结构参数与总体变形的关联程度。对参数化以后的数据进行Pearson相关性分析如表2所示。

表2 Pearson相关性分析

4.2 优化尺寸区间的确定

(1)分体外弧半径优化尺寸区间

将抽样得到的前后面板距离的样本数据与刀盘原始直径进行比值，将得到的比值数据与刀盘总体变形数据绘制关系图像，如图7所示。

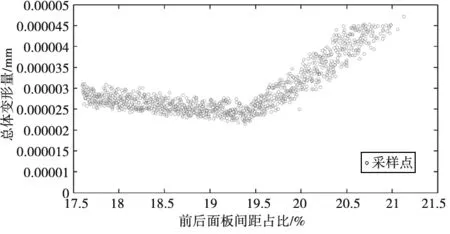
图7 分体前后面板间距与变形关系图

由图7可见，对于中方五分式刀盘，当考虑分体与中心体的耦合关系以及刀盘分体位置时，分体前后面板间距与总体变形关系呈现一种先平缓下降后大幅度上升最后趋于平缓的趋势；对于刀盘整体来说，当分体前后面板间距与刀盘直径比值在区间19.4%～19.7%时，总体的变形量最小，结构的稳定性最好，因此中方五分式刀盘进行整体设计时应选择分体外弧半径作为第一设计参数，并将其尺寸与刀盘直径的比值控制在19.4%～19.7%的范围内。

(2)筋板厚度的优化尺寸区间

为了研究在分体前后面板间距占比在最优区间内时，筋板厚度的最优化尺寸占比区间，采用影响系数的方法，首先将筋板厚度和前后面板间距与总体变形的相关系数相加，然后将各自的相关系数与相关系数的和相除得到加权系数，最后用加权系数乘以各自的尺寸并且相加得到一个综合影响结构尺寸参数，将其与刀盘直径进行比值处理，通过分析找到其最优化占比区间，之后再将筋板厚度占比区间还原出来得到筋板厚度的最优化占比区间。通过以上步骤得到的综合结构参数占比与总体变形量的关系如图8所示。

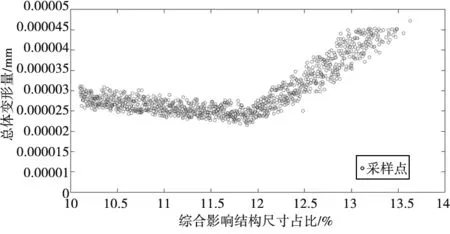
图8 综合影响结构尺寸占比与变形关系图

由图8可见，当综合影响结构尺寸占比在区间11.8%～12.1%时，总体的变形量最小，结构的稳定性最好，因此应将其尺寸占比控制在11.8～12.1%的范围内。然后，将筋板厚度占比区间进行还原可得其与刀盘直径的最优化占比区间为0.6%～0.79%。

5 结论

(1)创新性地提出了一种分体结构参数化优化方法，成功的将动力学分析与静力学分析进行了结合，并分析得到：当考虑刀盘各分体与中心体的耦合关系时，各个振动是存在差异的，分体轴向振动位移幅度最大，且切向振动幅度是其振动幅度的8.4%，分体法向振动幅度是其振动幅度的11.7%；

(2)当考虑刀盘分体与中心体的耦合关系时，前后面板间距和筋板厚度对分体的变形和稳定性影响较大，因此刀盘设计时可以优先考虑这两个尺寸的合理性；

(3)当考虑分体和中心体的耦合关系时，前后面板间距、筋板厚度、边板厚度、分体外弧半径与总体变形为正相关，而分体弧板厚度、前面板厚度、后面板厚度、连接板厚度与总体变形为负相关；

(4)TBM中方五分式刀盘设计时，当刀盘分体前后面板间距与刀盘直径的比值在19.4%～19.7%范围内，且筋板厚度与刀盘直径占比在0.6%～0.79%范围内时，刀盘分体结构变形最小，稳定性最好，因此为TBM中方五分式刀盘分体的结构设计和优化提供了有效的理论依据。