基于VMD_IWT近似熵与PSO_SVM的转子故障诊断*
2019-07-01张雪英刘秀丽栾忠权
张雪英,刘秀丽,栾忠权
(北京信息科技大学 现代测控技术教育部重点实验室,北京 100192)
0 引言
转子系统是旋转机械的核心部件,一旦发生故障,对机械设备的正常运行将产生直接影响[1]。因此,提高转子系统的故障诊断准确率具有十分重要的实际意义。
近年来,在转子故障诊断方面的研究越来越多。文献[2]提出了一种基于变分模态分解(VMD)的信号处理方法,通过处理后信号的频谱图准确诊断出转子存在的故障,但是没有进行不同种类故障的识别。文献[3]提出了自适应无参经验小波变换(APEWT)方法,将其与改进的归一化希尔伯特变换(INHT)相结合用于诊断转子局部碰磨故障。但APEWT存在轻微的端点效应。文献[4]将EEMD模糊熵与变量预测模型的模式识别方法发动机转子的信号分析及故障诊断,但EEMD较易受采样频率影响,且存在较大的分解误差。文献[5]采用Teager-VMD时频分析方法诊断了单盘转子的局部碰摩及油膜振荡现象,但在复杂工况下的应用有待进一步研究。
本文根据转子振动信号非平稳性、非线性的特征,提出了基于VMD_改进小波阈值的信号消噪方法,并提取近似熵作为特征向量,并结合粒子群优化的SVM进行诊断。实验表明,该方法对于转子故障诊断准确率达95%,证明所提方法具有一定的实际应用价值。
1 信号处理方法研究
1.1 变分模态分解(VMD)
VMD是由Konstantin Dragomiretskiy[6]于2014年提出的一种新的自适应信号处理方法,其核心思想是变分问题。约束变分模型表达式如式(1)所示[7]:
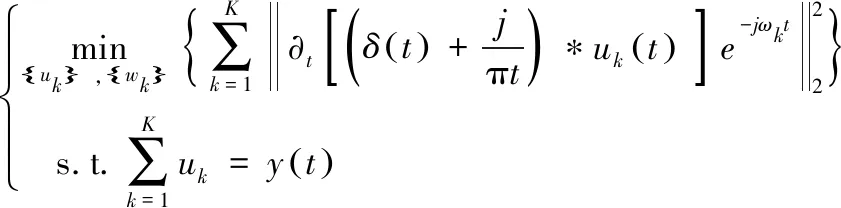
(1)
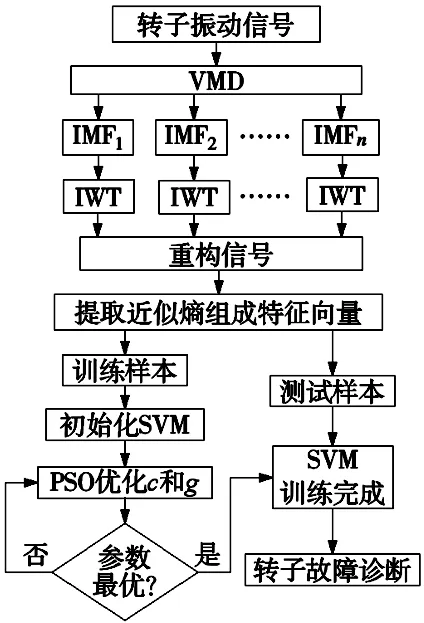
图1 故障诊断流程图
式中,{uk}>={u1,u2,…,uK}>为分解得到的K个IMF分量;{ωk}>={ω1,ω2,…,ωK}>为各分量的中心频率,y(t)为原始信号。为了将上述约束性变分问题转变为非约束性变分问题,使用拉格朗日乘子λ(t)和二次惩罚因子α对式(1)进行改造,得到扩展后的拉格朗日函数表达式为:
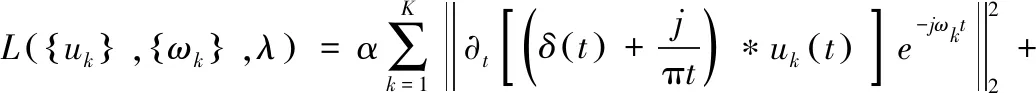
(2)
更新uk和ωk寻找约束变分问题的最优解,uk与ωk的最小化公式如式(3),式(4)所示。
(3)
(4)
1.2 改进小波阈值(IWT)
小波去噪的主要思想是以某一阈值处理小波分解后的系数,然后进行重构[8]。传统的小波阈值方法有硬阈值法和软阈值法。但其存在不连续问题和对于幅值较大的小波的衰减问题。针对以上缺陷,本文提出了IWT降噪方法。改进的阈值函数如式(5)所示。
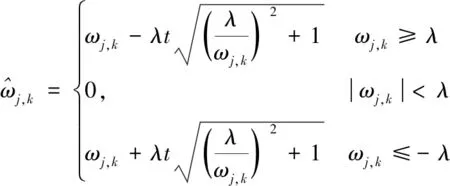
(5)
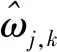
2 故障特征提取
本文提取处理后信号的近似熵组成特征向量进行故障诊断。近似熵值是用来表示序列复杂程度的标量,熵值越大,表明时间序列的复杂性越高,即信号的非平稳性越高,信号包含的频率成分越丰富,从而对信号的非线性和非平稳性进行量化[9]。近似熵值与数据长度N,维数m和阈值r有关,当m=2,r=0.1~0.2std(std为序列标准差)时,近似熵值对N的依赖程度较小。
3 基于PSO_SVM的转子故障诊断
SVM适用于小样本的机械故障诊断,惩罚参数c和核函数参数g为影响SVM分类性能的主要因子[10-12]。相较于其他核函数,RBF具有较快的学习速率和较强的分类能力,且使用时只需确定参数g。PSO迭代速度快,效率高,是求解最优问题的群体智能算法[10-12]。鉴于RBF与PSO的优势,本文选用RBF为核函数,选择PSO对参数c和g进行优化,以提高SVM的故障识别准确率。
VMD方法可以有效的避免模态混叠,IWT可以有效的滤除噪声,将二者结合起来,首先对转子振动信号进行VMD分解,得到若干IMF,对每个分量进行IWT降噪,对处理后的分量重构得到降噪后的振动信号。提取重构后信号的近似熵组成特征向量,输入PSO_SVM进行转子故障诊断。诊断流程图如图1所示。
4 实验分析
为了验证本文所提方法的有效性,采用本特利RK4微型转子试验台采集实际转子故障信号,实验平台如图2所示。实验用采集器为具有4通道同步采集功能的INV3062采集器,采样频率为20.48kHz。通过该实验平台采集转子不平衡,基础松动,正常及转子碰摩四种状态数据样本各60组,共计240组,每组数据1024个点,开展转子故障诊断分析。

图2 转子实验平台
4.1 VMD_IWT信号处理
以转子不平衡振动信号为例,选取一组信号(8000个数据点)进行分析,原始振动信号时域图如图3所示。
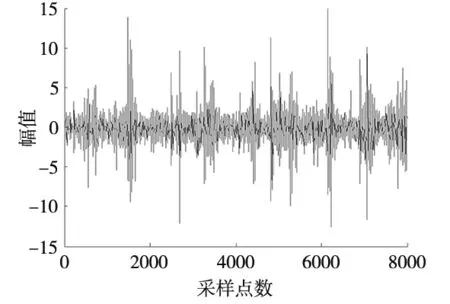
图3 转子不平衡信号时域图
对信号进行VMD分解,根据经验,惩罚因子α为2000,判别精度ε为10-6,经实验模数K的值选为4。图4~图5为转子不平衡振动信号经VMD分解后的时域波形与频谱图。
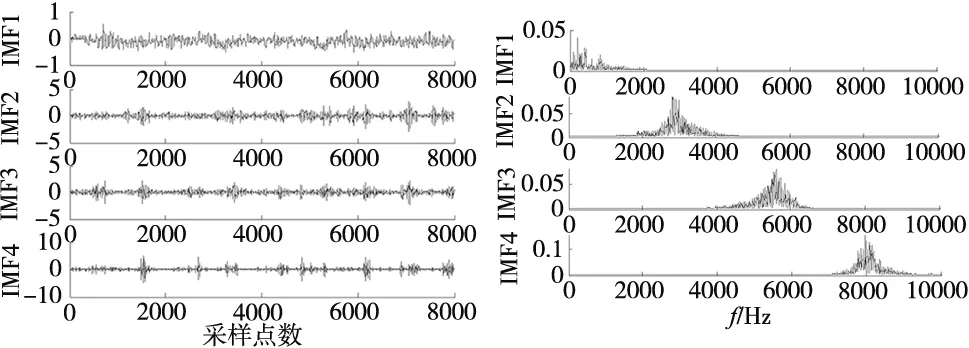
图4 VMD处理后时域波形 图5 VMD处理后频谱
由图5可知,VMD分解有效地避免了模态混叠。将VMD分解后的分量分别进行IWT降噪,并将降噪后的信号重构,重构后的转子信号如图6所示。
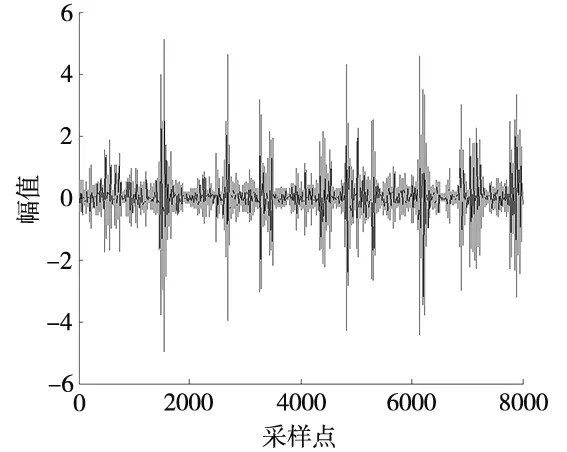
图6 重构信号时域图
对比图3和图6可知,VMD_改进小波阈值有效的滤除了噪声,更加凸显了信号中的冲击成分,有助于提高转子故障诊断准确率。
4.2 故障特征提取
将采集到的240组振动信号按照4.1节方法均进行VMD_IWT处理,提取处理后信号的近似熵作为特征值组成特征向量,将特征向量可视化以进行更加清楚的分析比较,如图7所示。
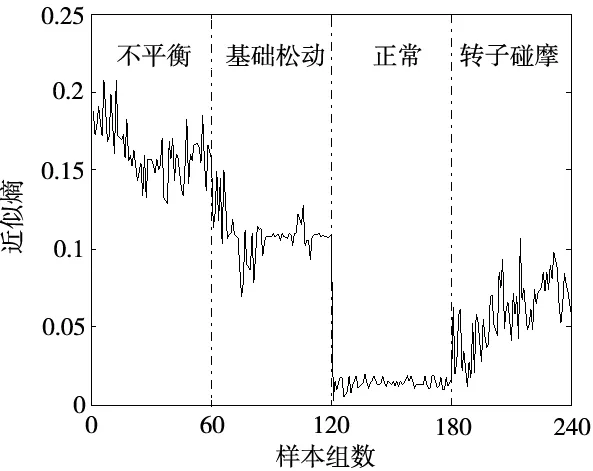
图7 转子故障特征向量
4.3 基于PSO_SVM的转子故障诊断
建立PSO_SVM网络模型,从每种状态下的60个特征值中随机选取40个作为样本,共160个,剩余20个作为测试样本,共80个,进行故障诊断。PSO寻找惩罚参数c和RBF核函数参数g的最终适应度曲线如图8所示,故障诊断结果如图9所示。

图8 适应度函数的最佳 适应度进化 图9 基于PSO_SVM的转子 故障诊断结果
由图9可知,只有4个样本识别错误,本文所提方法对转子故障识别识别的平均正确率达95%,具有较好的识别效果。
4.4 对比分析
为了证明本文所用VMD方法的有效性,将采集的240组转子振动信号首先进行EMD_IWT、LMD_IWT、EEMD_IWT处理,提取处理后信号的特征向量,分别输入BPNN、PNN、SVM、GA_SVM和PSO_SVM进行故障诊断,结果如图10所示。
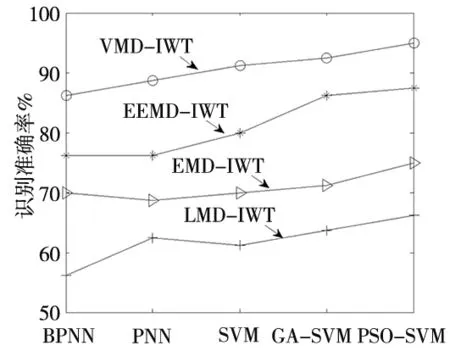
图10 基于不同分解方法与神经网络的故障诊断结果
可以看出,对于同一种神经网络,基于VMD_IWT降噪的转子故障诊断准确率最高,证明了VMD方法的有效性;对于同一种信号降噪方法,基于PSO_SVM的转子故障诊断准确率最高,达95%,证明了PSO_SVM方法的有效性。
为了证明本文提出的改进小波阈值方法的有效性,VMD分别与硬阈值与软阈值函数小波方法结合进行240组振动信号降噪并提取特征值组成特征向量,分别输入五种神经网络进行故障诊断,结果如图11所示。
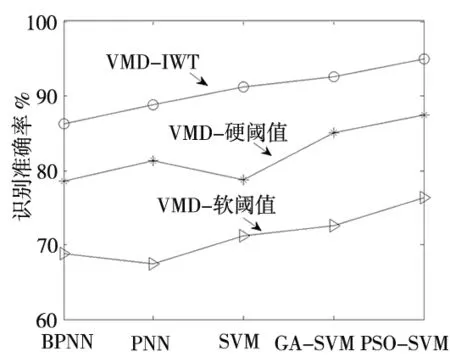
图11 基于不同阈值函数与神经网络的故障诊断结果
可以看出,对于同一种神经网络,VMD与改进小波阈值结合降噪的转子故障诊断准确率最高,证明了改进小波阈值的有效性;对于同一种信号降噪方法,基于PSO_SVM的转子故障诊断准确率最高,证明了PSO_SVM方法的有效性。
5 结论
本文针对转子故障诊断问题,提出了一种VMD_IWT近似熵与PSO_SVM相结合的故障诊断方法。对振动信号进行VMD_IWT降噪处理,提取处理后信号近似熵作为特征向量并输入PSO_SVM进行转子故障诊断。通过对实际转子振动信号进行分析,得出如下结论:
(1) 当与同一种神经网络结合时,VMD_IWT降噪后的转子故障诊断诊断准确率均高于EEMD_IWT、EMD_IWT、LMD_IWT,证明了VMD方法的有效性。
(2) 对于同一种神经网络,VMD与3种小波阈值结合时,VMD_IWT的故障诊断准确率最高,证明了IWT方法的有效性。
(3) 对于同一信号处理方法,基于PSO_SVM的故障诊断准确率均高于BPNN、PNN、SVM、GA_SVM,证明了PSO_SVM方法的有效性。
