还原数学细节：高斯推导正态分布概率密度函数的过程

杨 军，周菊玲

(新疆师范大学 数学科学学院，新疆 乌鲁木齐830017)

一、引言

正态分布是应用最广泛的连续概率分布，因其概率密度函数解析式

是由德国著名的数学家、统计学家高斯(Gauss.C.F，1777-1855)推导出来，故又称其为高斯分布(图1)。其也是高斯所有科学贡献中对人类文明影响最大者，故在欧元出现前的德国10马克的纸币上，不仅印有高斯的头像，更印有高斯分布N(μ，σ2)的密度曲线(图2)。

但是，如此不常见的密度函数解析式高斯究竟是源于什么思路想到，又是利用什么方法推导出来的呢？笔者就曾因学生在课堂上提出这个问题无法解释而尴尬不已……

后来直至有机会查阅到陈希孺院士所著《数理统计学简史》等[1-2]，其概要了高斯推导正态分布密度函数的思想方法，由此细细揣摩才发现历史上高斯对正态分布密度函数的推导源于对误差分布规律的研究，推导过程用到了“最大似然估计法”(今天的称谓)和初等微积分的相关知识。至此才还原了高斯推导这条曲线解析式的思路和数学细节。

图1 高斯分布图

图2 德国10马克纸币图

本文首先介绍相关预备知识，然后扼要梳理正态分布密度函数发现的历史脉络，并重点分析高斯推导正态分布密度函数的思想方法，据此还原高斯推导正态分布密度函数的数学细节和过程。

之所以介绍相关预备知识并重点关注高斯推导正态分布概率密度函数的数学细节和过程，是基于查阅正态分布历史的相关文献，大多关注其发展脉络和重大事件，鲜有从数学细节视角详细阐述高斯推导正态分布概率密度函数过程的文献。当然，作为统计学史方面的文献不应也不可能把历史上所涉及的数学细节均予以还原[3]。但如果历史上统计学家研究某个问题的解法具有史料价值，同时现有论著或文献又不易查到这样的解法，那么详细还原其数学细节和过程不仅具有历史意义，而且也具有数学逻辑价值。

二、预备知识

(一)最大似然估计法

设总体X的分布函数形式已知，但它的一个或几个参数未知。借助于总体X的一个样本值x1，x2，…，xn估计总体未知参数值的问题称为参数的点估计问题。最大似然估计法是其中常用的方法之一。

最有可能发生的事件最容易发生。设x1，x2，…，xn是总体X的一个样本值，那么既然已经取到总体X的一个样本值x1，x2，…，xn，则有足够理由认为样本值x1，x2，…，xn发生的概率比较大，从而就可以根据已经取到样本值x1，x2，…，xn的概率比较大这一朴素认识，去估计总体X的未知参数值。

根据以上朴素认识，英国统计学家费希尔(R.A.Fisher，1890—1962)于1912年提出了最大似然估计法：既然已经取到总体X的一个样本值x1，x2，…，xn，这表明取到这一样本值的概率较大，而不用考虑那些不能使样本出现的参数值θ作为其估计值。另一方面，如果当参数取θ0时，样本值x1，x2，…，xn的概率取很大的值，而其他的参数值θ使此概率取很小值，自然认为取θ0作为参数的估计值较为合理。由概率最大的事件最容易发生，从而有理由认为取到样本值x1，x2，…，xn的概率最大。进而根据其概率最大，去估计总体X的未知参数的值也就最为合理。

若总体X属于连续型，其概率密度函数f(x;θ)，θ∈Θ的形式已知，θ为待估参数，Θ是θ可能取值的范围。设X1，X2，…，Xn是来自X的样本，x1，x2，…，xn是相应于样本X1，X2，…，Xn的一个观测值，则随机点(X1，X2，…，Xn)落在点(x1，x2，…，xn)的邻域(边长分别为dx1，dx2，…，dxn的n维立方体)内的概率近似地为

(1)

这样，确定最大似然估计值的问题就归结为微分学中的求最大值问题了。注意到样本的似然函数L(θ)为连乘形式，通常对其取对数化为和的形式便于求最大值。

(二)两个引理

引理1 已知连续函数g(x)是定义在R上的奇函数，对任意自然数m及实数x，均有g(mx)=mg(x)，则g(x)=cx(其中c=g(1)为常数)。

下面利用“爬坡法”严格证明之。

证明(1)当x=0时，引理显然成立。

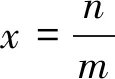
表明引理亦成立；

当x为任意负有理数时，由g(x)为奇函数易知引理仍然成立。

表明当x为任意无理数时，也有g(x)=cx。

综上，对任意实数x，均有g(x)=cx。

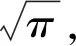
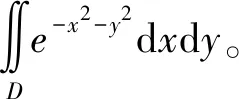
设D1={(x，y)|x2+y2≤R2}，D2={(x，y)|x2+y2≤2R2}，S={(x，y)|-R≤x≤R，-R≤y≤R}。

显然D1⊂S⊂D2。由于e-x2-y2>0，故在D1，S，D2上的二重积分之间有下列不等式：

(2)

令R→+，上式两端趋于同一极限π，从而

三、早期数学家与天文学家的相关工作

(一)数学家亚伯拉罕·棣莫弗的工作

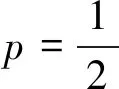
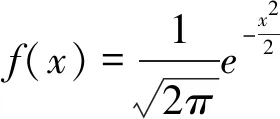
(二)天文学家关于误差分布规律的早期研究

历史上高斯对正态分布密度函数的推导源于对误差分布规律的认识。但在其之前，很多天文学家已经开展了相关研究。

伽利略(G.Galileo，1564—1642)可能是第一个提出随机误差概念并对其有所研究的学者[5]。他在1632年出版的著作《关于两个主要世界系统的对话》中提出:

(1)所有观测值都可能有误差，其源于观测者、仪器工具及观测条件等；

(2)观测误差对称地分布在0的两侧，因仪器工具使得观测值比真值大或小的可能性是等同的；

(3)小误差出现的频率大于大误差。

辛普森(T.Simpson，1710—1761)基于当时天文学家认为“因为不同天文台的设备和观测条件、人员素质上的差异导致观测结果的可靠性也有差异，故取算术平均值会受到‘坏’的观测值的干扰”，故而于1755年《在应用天文学中取若干观测平均值的好处》一文中第一次从概率角度严格证明了算术平均值的优良性：即在概率意义下，观测结果的平均误差比单次测量的误差小。辛普森上述工作并未触及建立一般的误差分布理论，他只是在误差满足某种特定分布的前提下，去计算平均误差的分布，从而证明观测结果的平均误差小于单次测量的误差。

拉普拉斯(P.S.Laplace，1749-1827)则直接研究误差论的基本问题“误差分布应取怎样的分布，以及在决定了误差分布后，如何根据多次观测结果去估计真值”。为此他提出误差分布函数f(x)应满足以下条件：

(1)f(-x)=f(x)；

(3)-f'(x)=mf(x)，x≥0。

关于条件(3)，拉普拉斯是基于“随着x→+，曲线f(x)下降且愈来愈平缓，故而其下降率-f′(x)也应随x增大而下降，同时-f′(x)与f(x)在下降中总保持恒定比例”。据此，拉普拉斯推出今天教科书中称之为拉普拉斯分布或指数分布的函数

随即拉普拉斯依据其确定的误差分布函数通过观测结果去估计真值。设被测的量真值为θ，则n次独立观测真值θ得到观测值x1，x2，…，xn的概率与

f(x1-θ)f(x2-θ)…f(x2-θ)

成正比例，但最终拉普拉斯因超级繁杂的计算无功而返。

四、高斯推导正态分布概率密度函数

(一)高斯推导正态分布概率密度函数的思想方法

高斯推导正态分布概率密度函数解析式的思想，与伽利略、辛普森、拉普拉斯等一样，也源自对误差分布规律的认识。1809年，高斯发表了其数学和天体力学的名著《绕日天体运动的理论》。在此书末尾，他写了一节有关“数据结合”(data combination)的问题，实际涉及的就是误差分布规律的确定问题。

高斯也提出了关于误差分布函数f(e)的几点看起来很自然的假定：

(1)所有的测量值相互独立且没有理由怀疑一个测量值比另一个看上去更不精确；

(2)误差分布密度函数连续且关于原点对称；

(3)当误差e的绝对值|e|→时，f(e)→0。

设θ是总体真值，x1，x2，…，xn是n次独立测量值，高斯把“n次观测真值θ得到独立观测值x1，x2，…，xn”的概率(实际是成正比例)取为：

L(θ)=f(x1-θ)f(x2-θ)…f(xn-θ)

(3)

其中f(x)为待定的误差分布函数。到此为止高斯的作法与拉普拉斯完全相同。

f(x2-θ)…f(xn-θ)

(4)

而反过来的问题是：如何求误差分布密度函数f(x)？对此，高斯提出了第二点出人意料的想法使其以极为简洁的方式推导出了误差分布密度函数f(x)。高斯认为：“当我们在相同的环境下，以相同的谨慎程度得到某一数量的多个直接观察值时，认为算术平均值为这一数量最可能的取值是大家通常都接受的公理。虽然这样做可能是不严格的，但至少是非常近似准确的，因此坚持这一点总是最稳妥的。”[2]

(二)高斯推导误差分布概率密度函数的数学细节和过程

函数L(θ)=f(x1-θ)f(x2-θ)…f(xn-θ)的最大值问题等价于：

(5)

(6)

故要求f(x)，只需求g(x)。由f(x)为偶函数，知g(x)为奇函数，即g(-x)=-g(x)。

g(mx)=mg(x)。

(7)

显然式(7)对一切自然数m及实数x均成立。从而根据引理1，可知g(x)=cx，即

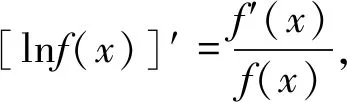
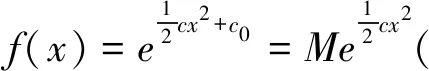
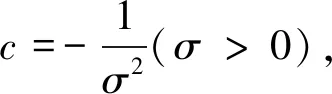
至此，数理统计学中最重要的统计模型“正态分布概率密度函数”终于露出了庐山真面目，并最终成为19世纪数理统计学的统治者。