Yule-Walker估计法的敏感性分析及其稳健改进

王志坚，王斌会

(1.广东财经大学 a.统计与数学学院；b.大数据与教育统计应用实验室，广东 广州 510320； 2.暨南大学 管理学院，广东 广州 510632)

一、引言

受随机因素的影响，金融时间序列中通常会含有异常值(outliers)，也称为离群值。如:突发的金融危机、人为的观测差错等。从现有文献来看，时间序列离群值分类较多，但考虑到影响水平与处理效果，可加型异常值(简称AO)和新息型异常值(简称IO)仍是最为主流的离群值研究对象。Box等曾指出，在建立时间序列模型时，离群值会影响模型识别及统计推断，导致基于该模型的预测和控制均有误。故有必要建立一种稳健的时间序列模型。为此，许多学者对其进行了研究。

关于如何建立一个稳健的时间序列模型，目前学术界主要有以下两种思路：一是离群值诊断方法，二是稳健统计方法。前者基本原理是先对离群值进行检测并剔除之，而后再采用经典估计方法建立模型。主要有：Karioti和Caroni采用似然比以及设定临界值方法来诊断AO型异常点[1]。Chareka等建立基于Gumbel分布统计量检验AO[2]。Louni通过扩展Abraham和Yatawara的AO及IO型离群值检测法，采用修正次序检测法对ARMA模型离群值进行检测，效果要优于改进前，特别是对IO型离群值[3]。Nare等用Gumbel分布作为极限分布来检测和校正离群值[4]。王志坚和王斌会将Chen等提出的AO型异常点检测统计量进行稳健改进，改进后检测效力显著提高，其主要方法就是用绝对离差均值替代标准差[5]。

稳健统计方法，即当数据中含有离群值时，基于该方法得到的时序模型参数估计值几乎不受影响或变化轻微。学者们常用的稳健回归参数估计方法主要有：M估计、GM估计、S估计、RA估计与MM估计等[6-11]，以及基于辅助AR模型的间接推断法、稳健滤波法等[12-13]。王志坚基于FQn统计量对传统自相关函数进行改进，构建出自回归AR模型的稳健估计算法，以克服离群值的影响[14]。袁海静研究了计数时间序列模型的稳健估计问题[15]。

对于时间序列AR模型的稳健估计法目前最为流行的是Huber提出的基于成对协方差的稳健自相关函数法，下文将该方法简称为Huber稳健法。本文首先分析了AR模型Yule-Walker估计法(以下简称Y-W估计法，全文适用)的不稳健性。其次基于均值和方差的稳健估计量组合构建了稳健自相关函数，从而得出时序AR模型的稳健Y-W估计法。最后将本文提出的基于稳健Y-W稳健估计法与Huber提出的稳健估计法以及AR模型四种经典参数估计方法：最小二乘、最大熵谱法、极大似然和Y-W估计法进行模拟和金融数据实证对比，发现当对含有异常值的时间序列建立AR模型时，本文提出的稳健估计方法得出的结果要显著优于传统估计法。全文用R语言进行统计分析。

二 、AR模型的Yule-Walker估计法及其敏感性分析

Y-W估计法(也称为矩估计法)是时间序列AR模型常用的参数估计方法之一，关于Y-W估计法的敏感性问题，文献[14]已有部分相关阐述。考虑到后面研究的需要，将其原理梳理一遍。考虑如下零均值AR(p)模型：

xt=φ1xt-1+φ2xt-2+…+φpxt-p+et

(1)

其中，φ1，φ2，…，φp为待估参数，为估计之，在式(1)两边同乘xt-j，j>0，得式(2)：

xtxt-j=φ1xt-1xt-j+φ2xt-2xt-j+…+

φpxt-pxt-j+etxt-j

(2)

对式(2)两边取期望，得

Extxt-j=φ1Ext-1xt-j+φ2Ext-2xt-j+…+

φpExt-pxt-j+Eetxt-j

(3)

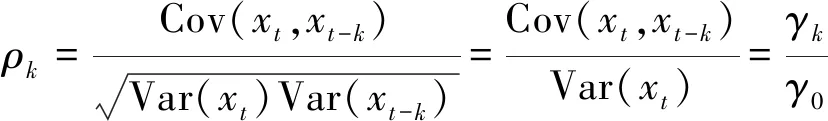
γj=φ1γj-1+φ2γj-2+…+φpγj-p

(4)

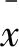
ρj=φ1ρj-1+φ2ρj-2+…+φpρj-p

(5)

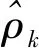
(6)

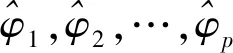
(7)

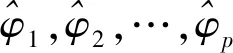
通常，对于弱平稳时序xt与xt-k，其自相关系数可记为：

因为xt为弱平稳，所以上式有Var(xt)=Var(xt-k)，根据定义有ρ0=1，ρt=ρ-t。而集合{ρk}称为xt的自相关函数。 Y-W估计法的最主要部分是样本自协方差函数，即下面的式(8) ：

γk=Cov(xt，xt-k)

=E[(xt-Ext)(xt-k-Ext-k)]

(8)

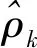
R语言包中自带的时间序列数据集data(lh)，共有48个观测值。在该观测值中随机抽取一个数，再用30去替代之，将30作为数据集data(lh)的离群值，同时分别对被污染前后的数据集data(lh) 计算其自相关函数值，相应的R代码与序列图如图1所示：

lh1=replace(lh，25，30) #在原始数据集lh上构造一个离群值30

plot(lh1，type="p"，ylim=c(0，31)) #含离群值的序列图(图1左)

text(25，28，expression(离群值)，adj=0)

par(mfrow=c(1，2)) #含离群值和不含离群值自相关函数图(图1中、右)

acf(lh)

acf(lh1)

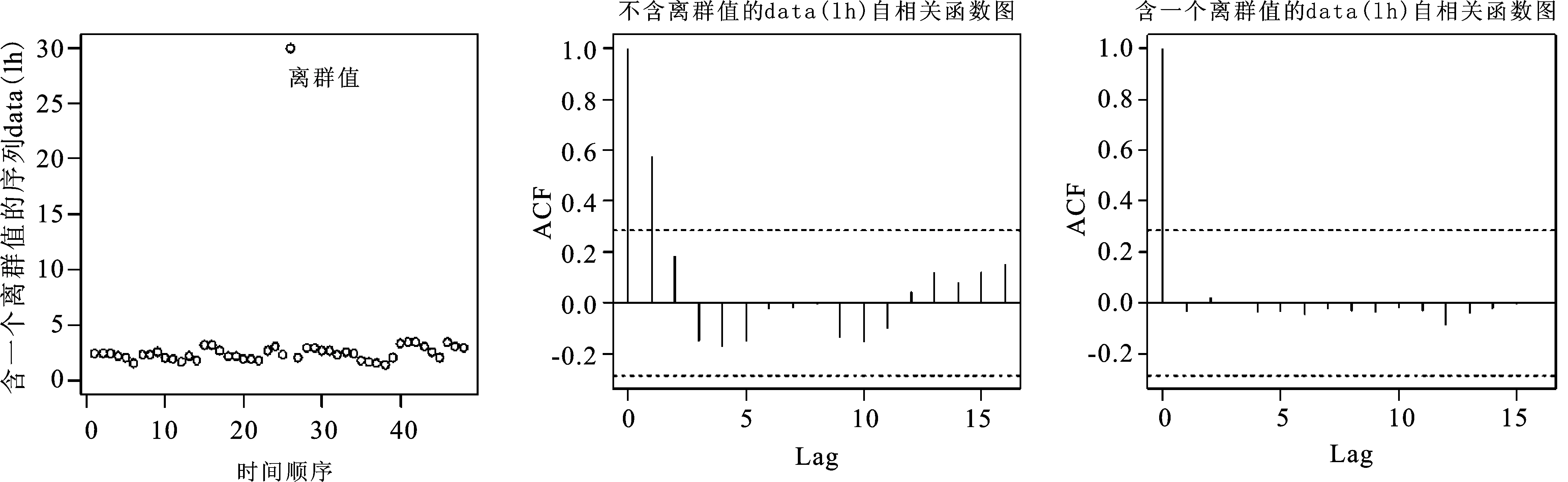
图1 含离群值时序图(左)与被污染前后的自相关函数图(中、右)

由图1可以看出，被污染前数据集data(lh)自相关函数图(中)与被污染后数据集data(lh)自相关函数图(右)相差较大，说明自相关函数对离群值很敏感，是不稳健的。另外，在模型识别中，通常根据ACF图来确定模型移动平均阶数，而从图1可以得出，由于一个离群值的存在，移动平均阶数已由原来的ma=1变为ma=0阶。即离群值会改变样本自相关函数值，同时对模型识别也有较大的影响。

三、Yule-Walker估计法的稳健改进及其模拟比较

(一)Yule-Walker估计法的稳健改进

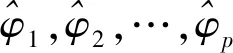
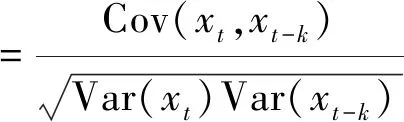
(9)

显然，式(9)中的均值Ext、Ext-k以及方差Var(xt)、Var(xt-k)都是不稳健的，它们对尾部数据和异常值非常敏感。因此，要构建稳健的自相关函数ρk，关键是要构建均值Ext、Ext-k以及方差Var(xt)、Var(xt-k)的稳健估计量。

均值常用的稳健估计量包括：

(1)切尾均值(TM)。假设x(1)≤x(2)≤…≤x(N)是样本顺序统计量，切尾均值TN(δ，1-γ)的定义为：

δ，γ∈(0，0.5)，LN=floor[Nδ]，UN=floor[Nγ]

(3)中位数(Med)。中位数Med(X)是样本顺序统计量中心位置的值：

方差常用的稳健估计量有：

(1)缩尾标准差(WSD)，表达式为：

缩尾标准差指的是缩尾数据的标准差。

(2)绝对离差均值(MeanAD)，表达式为：

显然，其稳健性体现在表达式中的中位数MED上。

(3)绝对离差中位数(MAD)，表达式为：

MAD=MED|X-MED(X)|

显然，其稳健性体现在表达式中的双重中位数MED上。

(4)四分位数间距(IQR)，表达式下：

IQR=Q(0.75)-Q(0.25)

其中，Q(0.75)和Q(0.25)分别是数据由小到大排序后的第三和第一分位数。其稳健性体现在数据排序后异常点被排在序列的两端，当异常点比例未达到总数据的25%时，异常点对IQR没有干扰。

基于以上3个均值稳健估计量、4个方差稳健估计量，本文经反复试验比较均值和方差稳健估计量的组合，发现当选取中位数(Med)为均值的稳健估计量，绝对离差中位数(MAD)为方差的稳健估计量时，自相关函数ρk的稳健估计效果最优，因此经典的样本自相关函数：

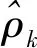
(10)

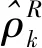
(11)

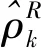
(12)

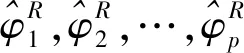
(二)模拟研究

下面用R语言模拟一个如下AR(2)序列：xt=5xt-1+2xt-2+et其中，φ1=5，φ2=2。残差et服从一个被均匀分布Uuiform(-16，16)污染的正态分布即：

et～(1-ε)N(xt;0，1)+εUniform(xt;-16，16)

ε为污染率，分别取如下不同的污染度：0，0.01，0.05和0.1，即从无污染、轻污染到重污染来探讨。样本量取100，500和1 000，即覆盖小样本、中样本到大样本来考虑，目的是综合来看稳健Y-W估计法对参数稳健估计效果。

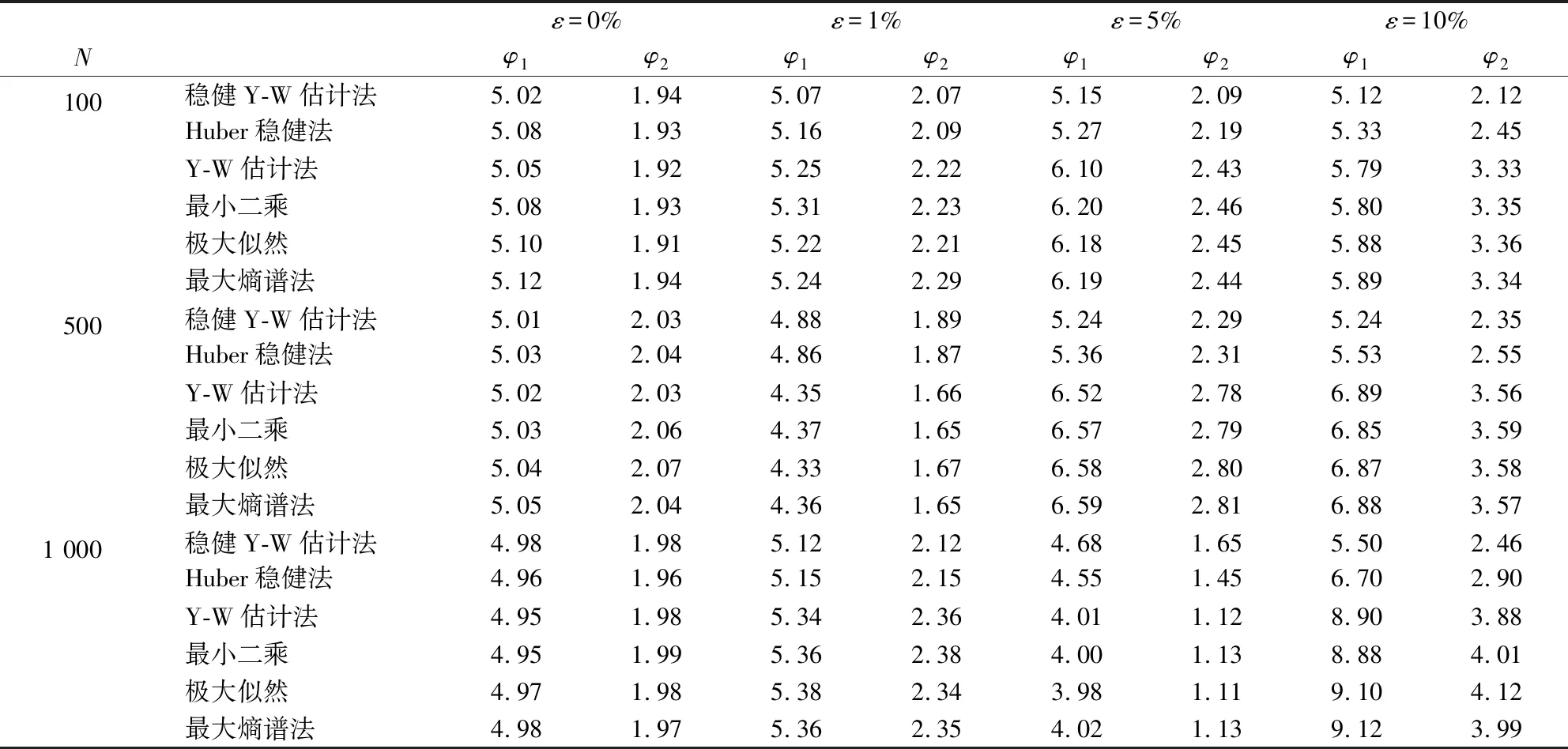
表1 不同污染率以及不同样本量下各估计法对AR(2)模型估计结果对比表

从表1可以看出，在样本数据无污染情况下，即污染率为0%时，样本量不同时，稳健Y-W估计法、Huber稳健法与AR模型的经典估计法对参数估计结果差别不大，均接近真值，说明稳健Y-W估计法具有可行性。当污染率为1%时，稳健Y-W估计法与Huber稳健法在不同的样本量下均比较接近真值，而其他四种估计法估计结果较接近，但偏离真值较大。值得一提的是，相比于中样本和大样本，小样本偏离更厉害。当污染率为5%时，稳健Y-W估计法与Huber稳健法虽在不同的样本量下相差不大，但稳健Y-W估计法比Huber稳健法更接近真值，而其他四种估计法基本一致，但与真值相差较大；当污染率为10%时，稳健Y-W估计法与真值有少许偏离，Huber稳健法偏离较大，而其他四种估计法已偏离的面目全非，而且样本量越大，偏离越厉害。因此，稳健Y-W估计法在大样本、重污染率下优势更明显。因此，从模拟结果看稳健Y-W估计法很好的验证了稳健估计的三个目标：第一，稳健估计在假定分布模型下得到的结果是最优的；第二，当假定分布与实际分布模型偏离较小时，离群值对模型的参数估计值影响是很小的；第三，当假定与实际分布模型偏离较大时，离群值不会对参数估计值产生致命影响。

四、实证检验

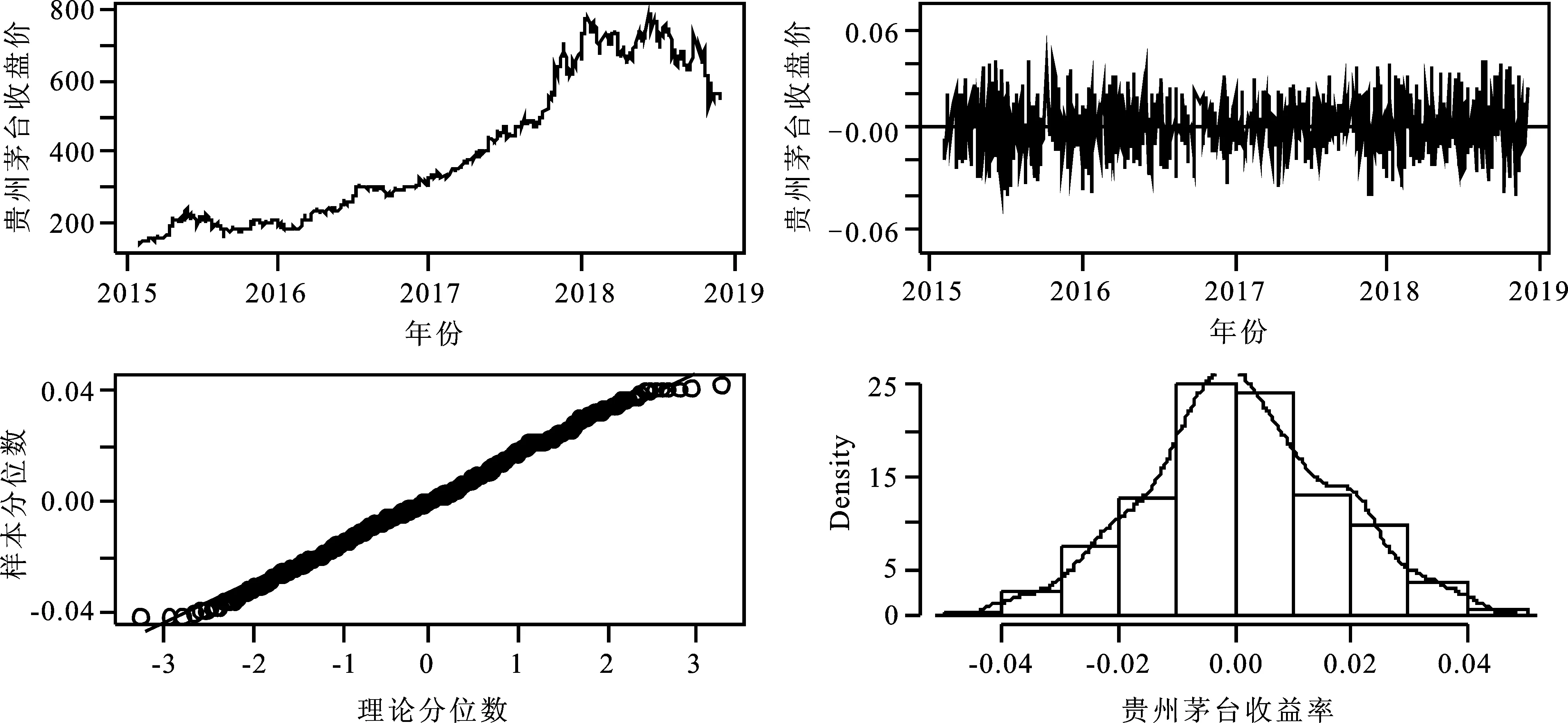
为检验本文提出的稳健矩估计法的有效性，下面选取上海证券交易所的一只股票-贵州茅台(简称GZMT)公司股票收盘价及收益率数据作为研究对象，研究区间为2015年2月4日至2018年11月30日，共933个样本数据，数据通过采用R软件从雅虎财经网站获取。先通过可视化方法对样本数据进行探索性数据分析，以期对收益率有大概了解，可视化结果如图2所示。

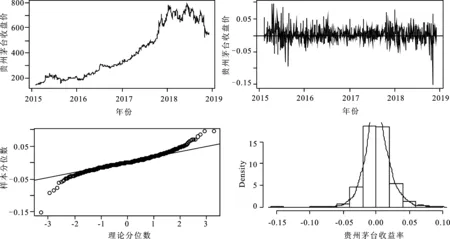
从图2的第一个收盘价图可以看出，2018年之前收盘价一直呈上升趋势，从2018年开始震荡并伴随有局部下降趋势。另外，从收益率图可以看出，收益率存在较多离群值，从收益率QQ图及直方图来看，两者均已明显偏离正态分布。可以推测，由于离群值的存在使得收益率偏离正态分布。同时，Shapiro-Wilk正态性检验结果显示，检验统计量值为0.954，p值接近0，拒绝收益率为正态性的原假设。因此，前面的探索性数据分析结论得到验证：收益率偏离正态分布是由于序列中含有离群值导致。

下面我们用文献[5]的时间序列异常值稳健检测方法对贵州茅台收益率进行异常值检测，共检测到16个异常值，其中IO型异常值7个，AO型9个，结果见表2。

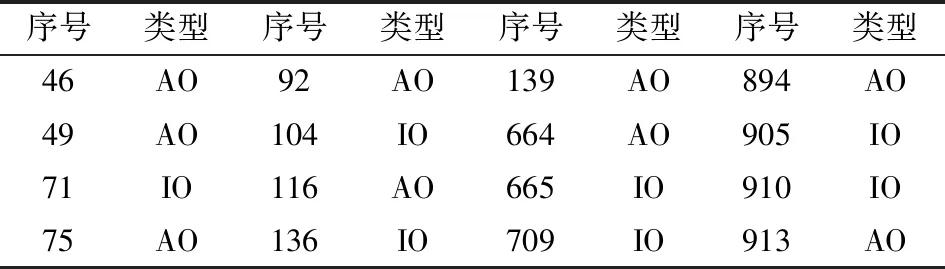
表2 贵州茅台公司股票收益率异常值检测结果表

从检测结果来看，异常值在总样本数据中所占的比重较小，仅为1.71%，但它确实客观存在，由前文分析可知，实际上单个较大的异常值就能将模型识别或参数估计变得面目全非，故对于含有异常值较小比重的时间序列采用稳健建模方法也是很有必要。在建模之前需要对收益率序列进行平稳性检验，用ADF单位根检验，检验结果见表3。

表3的检验结果非常显著，表明收益率序列是平稳的，可以用来建模。为防止模型识别错误，用稳健的识别法对模型进行识别，得出序列可拟合AR(2)模型。

表3 贵州茅台股票的日对数收益率ADF检验结果

对模型识别后分别用本文提出的稳健Y-W估计法与AR模型常用的四个估计方法对AR(2)模型进行参数估计，估计结果如表4所示：

从表4可以看出，对参数φ1与φ2的估计，四种经典估计方法很接近，但与稳健Y-W估计法相差较大，而Huber稳健法则介于四种经典估计方法与稳健Y-W估计法之间。该结果仅仅说明了稳健估计与非稳健估计之间的差别。而至于哪种方法更优，还有待于进一步论证。

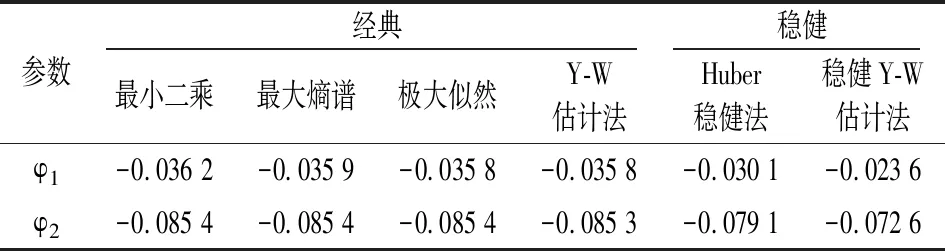
表4 稳健Y-W估计法与传统估计法对AR(2)模型估计结果对比表

接下来，我们将前面检测出的16个异常点剔除，考虑在无异常点情形下对比各估计法的估计效果。先对剩下的样本数据的收盘价及收益率数据做探索性数据分析图，如图3所示。

从图3可以看出，在删除被检测到的离群值后，收益率图与QQ图比删除前要整齐很多。而QQ图及直方图均说明删除离群值后的贵州茅台收益率序列比删除前更接近于正态分布。接下来，对删除离群值后的贵州茅台收益率序列同样采用本文提出的稳健估计法与Huber稳健法以及四种经典的估计方法进行参数估计，结果如下表5。

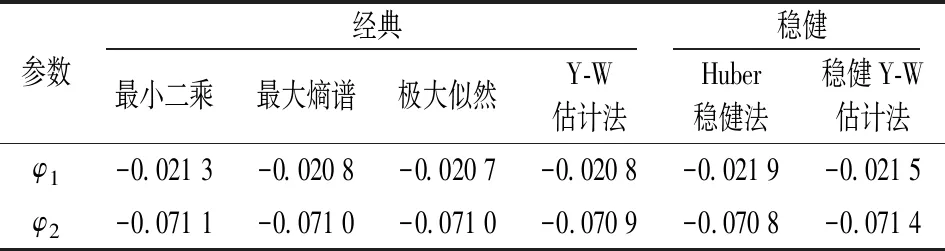
表5 删除离群值后稳健Y-W估计法与传统估计法对AR(2)模型估计结果对比表

从表5可以看出：对φ1，φ2的估计结果，四种经典估计法对与两种稳健估计法很接近。通过对比表4和表5的结果，可以看出删除离群值前后，四种经典估计法改变很大，Huber稳健法改变较大，而稳健Y-W估计法改变轻微。

以上结果也正好说明以下两点:一是当数据中不存在离群值时，本文提出的稳健估计方法与经典的估计方法对参数的估计结果几乎没什么差别;二是当数据中存在离群值时，稳健估计结果与真值非常接近，表现出一定的耐抗性，而传统的估计方法已变得面目全非。同时，说明经典估计方法对异常值敏感，而稳健估计克服了常规估计法的弱点，对异常值表现出了一定的耐抗性，因而估计结果是稳健的、可靠的。

五、结语

由以上模拟和实证分析结果可以看出，当金融时间序列中存在离群值时，用传统的参数估计方法建模、分析得出的结果往往与实际情况不符，甚至单个或多个离群值就有可能彻底改变我们对金融现象的判断。然而，金融时序中的离群值又通常隐含了重要的投资信息，故不能直接将其剔除。因此，在建模过程中为了使模型能够符合大多数数据表现出来的规律性，有必要构造一种稳健的参数估计量来克服离群值的影响。这即是本文研究的出发点。

文中首先从理论上分析了时间序列AR模型矩估计法(Yule-Walker法)的不稳健性。其次，构建了基于稳健均值与稳健方差的稳健自相关函数，得到了AR模型的稳健参数估计算法来克服离群值的影响。第三，将本文提出的稳健Yule-Walker估计法与Huber稳健法以及AR模型常用四种参数估计法：最小二乘、最大熵谱法、极大似然以及传统Yule-Walker法在三种污染率、三种样本量下进行模拟：发现在无离群值时，稳健Yule-Walker估计法、Huber稳健法与其他四种方法得到的结果基本保持一致；在有离群值时，其他四种方法得出的结果均出现很大变化，Huber稳健法变化较大而本文提出的稳健Yule-Walker估计法基本不变；特别注意到，在高污染率、大样本情形下，其他四种方法结果已变得面目全非时，稳健Yule-Walker结果只是变化轻微。

最后，选取贵州茅台股票从2015年2月4日至2018年11月30日的日对数收益率作为研究对象进行实证检验，检验结果与模拟结果基本一致，而本文提出的稳健Yule-Walker估计法能抵抗异常值干扰，是稳健的，可以运用于金融数据分析。