异方差帕克检验方法的改进

谭 馨，邓光明，b

(桂林理工大学a.理学院；b.应用统计研究所，广西 桂林 541006)

一、引言

回归模型的使用要满足的基本假定之一是方差齐性，而在大多数社会经济现象中，存在着大量的异方差数据，所以这种假定在实际经济观测值中常常不成立。因而如何发现并解决异方差性是建立回归模型中所关注的重要问题。在异方差的检验方法中，一般假定随机干扰项的异方差是由解释变量引起的，故本文针对线性回归模型中与解释变量有关系的这类异方差问题展开探讨[1]。

国内外学者关于这类异方差问题进行了大量的研究，得到了一些检验异方差的方法，如图示检验、斯皮尔曼等级相关系数检验、G-Q检验、帕克检验、格莱舍尔检验、怀特检验等[2-7]。其中，帕克检验方法不仅可以检验异方差是否存在，而且可以探测异方差的具体表达式，这有助于进一步研究如何消除异方差性的影响。对于一元线性回归模型来说，模型中只包含一个解释变量，利用帕克检验能快速确定异方差和解释变量的关系表达式。然而，对于多元线性回归模型来说，帕克检验仍然有很多不足，主要体现在以下三方面：其一，模型中包含多个解释变量，需要多次重复帕克检验的步骤来确定异方差和某个解释变量的具体表达式，这使得帕克检验方法的过程繁琐；其二，异方差可能和多个解释变量有关，而在帕克检验中每次只能和一个解释变量建立回归模型，用该方法就会得到多个异方差模型，这使得帕克检验得到的模型复杂；其三，解释变量之间可能存在相关性，利用帕克检验构造的多个异方差模型就不准确。因此，本文在传统的帕克检验的基础上，运用主成分的思想，将所有样本主成分代替单个解释变量建立异方差模型，在没有损失样本信息的前提下，消除自变量之间的相关性，再依据系数的显著性，给出新的异方差检验方法。为保证研究的完整性，下面先对异方差的定义和传统的帕克检验方法做简单介绍。

二、传统的帕克检验方法

(一)异方差性的定义

经典的线性回归模型可以表示为：

yi=β0+β1xi1+β2xi2+…+βkxik+μi

(1)

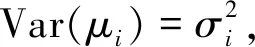
(二)帕克检验

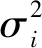
对于多元线性回归模型，帕克检验步骤[8]如下：

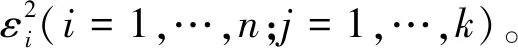
第二步，取异方差结构的函数形式为：

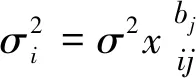
(2)

一共构建k个异方差模型(j=1，…，k)，其中bj为未知参数，vij是独立同方差的随机变量。则(2)式可以写成对数形式：

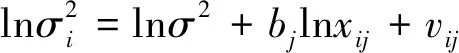
(3)

(4)

对模型(4)应用最小二乘法，得出lnσ2和bj(j=1，…，k)的估计值。

第四步，对bj进行t检验。原假设H0：任意bj=0(j=1，…，k)；备择假设H1：至少有一个bj≠0。如果存在bj显著，就表明原模型存在异方差；如果bj不显著，则可以接受同方差假设。

下面对帕克检验方法进行改进，使得改进后的方法更准确更简便地应用到多变量的异方差检验过程中。

三、改进的帕克检验方法

(一)新的异方差模型

上述传统的帕克检验方法通过构造k个异方差结构形式来检验原模型中是否存在异方差性，但解释变量间存在相关性，这导致构造的k个异方差模型不准确。基于此，我们提出对解释变量进行主成分分析。因为异方差与解释变量x1，x2，…，xk有关，主成分z1，z2，…，zk又是解释变量的线性组合，所以异方差与主成分有关。构造一个新的异方差结构的函数形式为：

(5)

共构建k个异方差模型，其中bj(j=1，…，k)为未知参数，vij是独立同方差的随机变量。需要指出，式(5)中对主成分zij(j=1，…，k)取绝对值是因为xij虽然是为正数的经济数据，但xij线性组合后主成分zij中可能出现负数，而异方差是平方数，且方差是用来反映数据的波动情况，仍然以未加绝对值的主成分zij的均值为基准值，原本负数主成分zij负向波动，加上绝对值后变成正向波动，并不影响呈现异方差的效果。

将式(2)和式(5)进行对比可知，在传统的异方差结构式中，由于解释变量x1，x2，…，xk存在相关性，所以构造的k个异方差模型中存在重叠信息，且无法把k个异方差模型中有效信息部分提取出来；而式(5)所构造的k个新的异方差结构中没有重叠信息，可以提取异方差的有效部分。但式(5)的异方差结构需要构造k个模型，仍然需要大量重复拟合的工作量。

进一步对异方差结构进行研究，类比概率论知识，对于n个相互独立的随机变量X1，X2，…，Xn，如果总体X具有分布函数F(x)，则随机变量(X1，X2，…，Xn)具有联合分布函数[9]：

(6)

(7)

对式(7)开k次方根，得到新的异方差函数结构形式：

(8)

由式(8)可知，如果异方差和某个主成分zij相关，那么bj≠0(j=1，…，k)显著，则原模型中存在异方差性。反之，如果异方差和任意一个主成分zij都不相关，那么bj=0不显著，则原模型中不存在异方差性。对比在传统的帕克检验中，用式(2)完成异方差检验需要构造k个异方差模型；而在改进的帕克检验方法中，用式(8)只需构造1个异方差模型，此方法更为简便。

(二)改进的帕克检验方法的步骤

根据上述新的异方差模型的构造，得到改进的帕克检验方法的具体步骤如下：

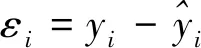
步骤2：对回归模型中所有的解释变量进行主成分分析，主成分可以由原来的解释变量线性表示，即满足下式：

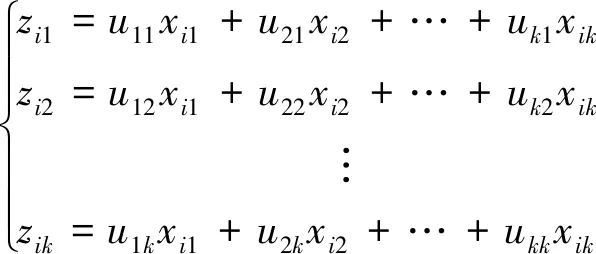
(i=1，2，…，n)

(9)

其中k为解释变量的个数。

步骤3：取异方差结构的函数形式如公式(8)，该式可以写成对数形式：

(10)

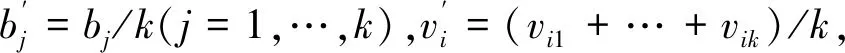
(11)

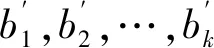
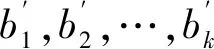
对比传统的帕克检验，改进的帕克检验方法的优势在于：一是直接用残差序列与所有主成分建立异方差模型，不需要多次重复帕克检验的步骤，大大减少了计算量；二是用所有主成分代替单个解释变量建立异方差模型，既保留样本所有的信息，又解决了解释变量间存在相关性的问题；三是简单明了地体现了异方差和哪些主成分有关，通过主成分和解释变量前系数的大小，确定主成分与解释变量之间的相关性，继而确定引起异方差的主要解释变量，解决了传统帕克检验用多个模型来说明异方差的问题。下面用模拟数据对该方法进行验证。

四、随机模拟

(一)生成模拟数据

生成随机模拟数据[1]。设定三组样本变量x1、x2、x3全部是均值为0、方差为1且服从正态分布的变量，样本容量为500。考虑到3个变量间的相关性可能会对检验结果造成影响，因此在生成数据时额外设定了两两之间的协方差(方差为1，即为皮尔逊相关系数)，依次为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9。设定参数b0=6，b1=8，b2=2，b3=3，被解释变量yi生成的表达式为：

yi=6+8xi1+2xi2+3xi3+μi(i=1，…，500)

(12)

其中μi为500个来自均值为0的正态随机项，设定的该随机项形式为

μ=x1ξ

(13)

其中ξ为服从标准正态分布的、相互独立的随机变量。显然，μ这类随机项的形式极易产生异方差问题，且异方差和解释变量x1有关。

(二)异方差性检验

用R软件按上述机制生成模拟数据，对生成的数据分别进行传统的帕克检验和改进的帕克检验。

1.传统的帕克检验。对解释变量x1、x2、x3与μ2进行对数处理，根据(4)式分别建立3个异方差模型：

(14)

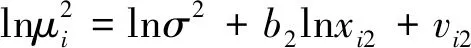
(15)

(16)

对模型(14)～(16)使用最小二乘法实现系数估计。用P值检验模型中系数b1，b2，b3的显著性。将得到的P值与α=0.05 比较，如果b1，b2，b3中存在系数显著，就表明模型存在异方差性，反之，满足同方差假定。

2.改进的帕克检验。对解释变量x1、x2、x3做主成分分析，将得到的所有主成分与μ2进行对数处理，根据(11)式对新数据建立异方差模型：

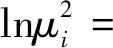
(17)

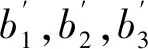
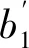
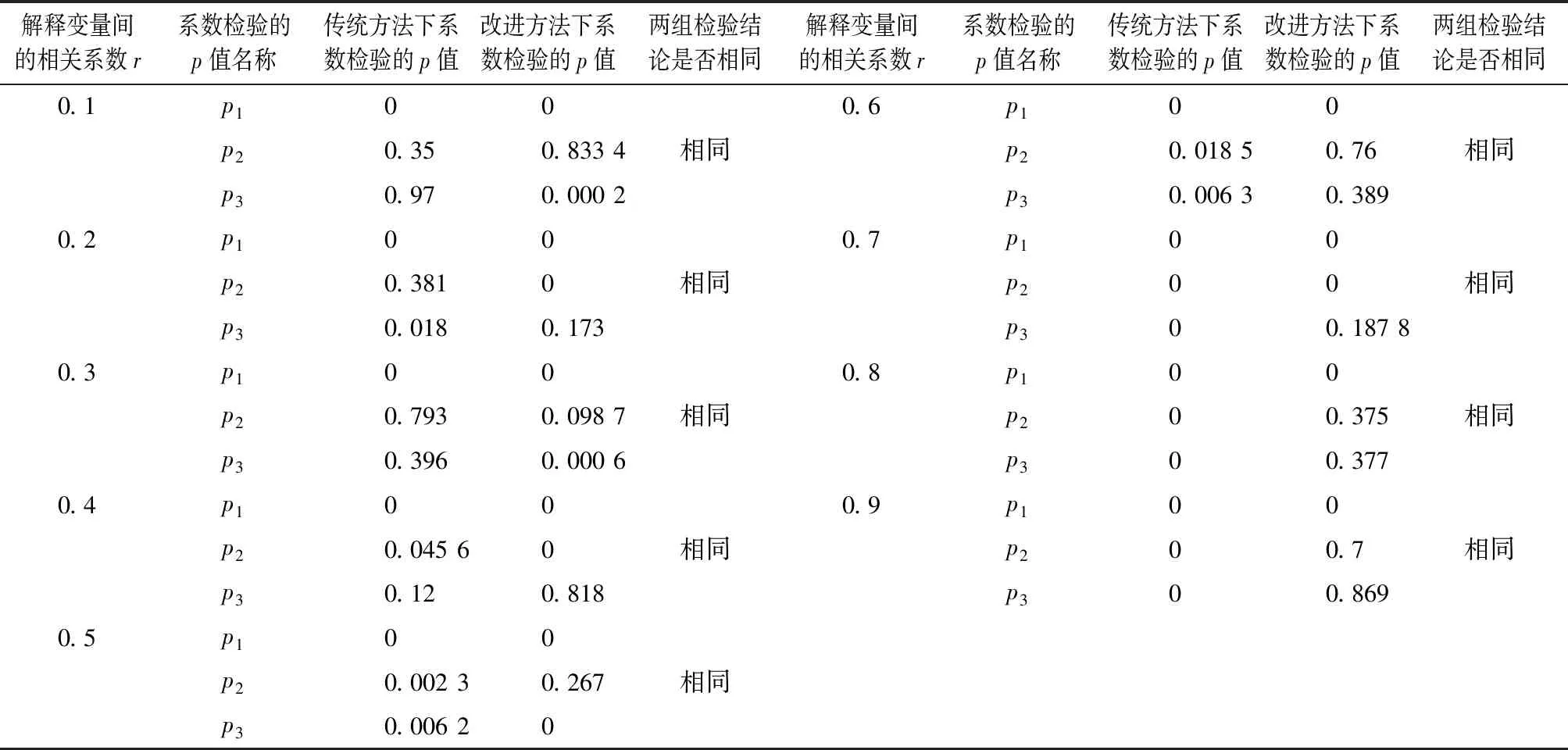
表1 模型中系数的显著性检验(1次模拟)表

从两方面来看表1中系数检验的结果：

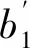
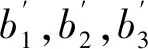
进一步在每个相关系数场合下进行10000次随机模拟实验，并用模拟数据进行异方差检验，将传统的帕克检验与改进的帕克检验进行对比，检验结果如表2：

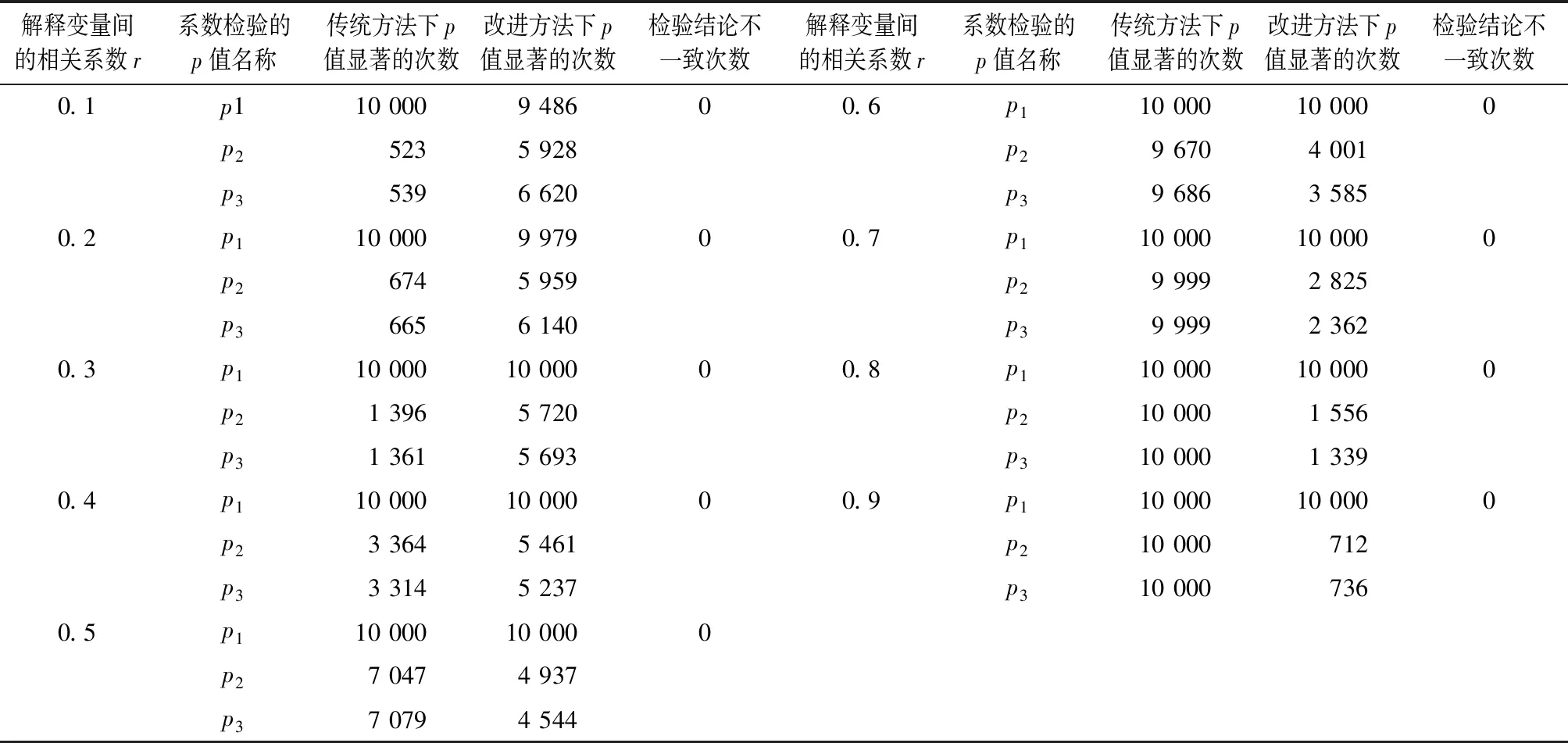
表2 模型中系数的显著性检验(10 000次模拟)表

从表2中得到如下结论：

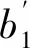
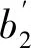
综上，可以看出这两种方法的差别：当解释变量间的相关程度越高，传统的帕克检验得到显著的系数个数越多，而改进的帕克检验得到显著的系数个数就越少，这是因为传统的帕克检验要对x1、x2、x3这3个解释变量分别建立异方差模型，设定的随机变量又与x1有关，即异方差与x1有关，随着解释变量x1与x2、x3相关程度越高，随机变量也与x2、x3相关，这使得异方差也与x2、x3有关，继而得到的每一个异方差模型中的系数都显著；而改进的帕克检验将变量进行主成分分析，得到几个相互无关的综合变量，随着解释变量间的相关程度越高，重叠的信息就越多，进而得到的综合变量中第一主成分就包含了绝大部分的信息，剩下的主成分只包含很小一部分信息，即得到的显著的系数个数就越少。从表2也能看出，随着解释变量间的相关程度达到0.8时，传统的帕克检验得到的检验结果为异方差与x1、x2、x3都有关，这与设定的随机变量与x1有关这一结论存在偏差；而改进的帕克检验随着解释变量间的相关程度越高，得到的检验结果为异方差与第一主成分有关，通过第一主成分和解释变量之间的相关性，继而确定引起异方差的主要解释变量，这一过程将在下一部分实例分析中得以具体展示。综上所述，改进的帕克检验不仅简化了传统帕克检验的步骤，而且随着解释变量间的相关性增强，其得到的检验结果要优于传统的帕克检验。

为保证模拟的严谨性与完整性，笔者还拟合了皮尔逊相关系数为-0.1、-0.2、-0.3、-0.4、-0.5、-0.6、-0.7、-0.8、-0.9等9种情况，证明正负关系不影响最终结论，文中没有列出相关系数为负数的情形，以节约篇幅。

五、实例分析

从国家统计局中收集2017年31个地区人均地区生产总值y、人均居民消费支出x1、人均社会消费品零售总额x2(社会消费品零售总额除以年末常住人口)和人均地方财政一般预算支出x3(地方财政一般预算支出除以年末常住人口)数据，单位均为万元。为了更有效地观察残差和拟合值之间的相关性，对所有数据按人均地区生产总值升序进行排序。

首先，构建用于研究影响人均地区生产总值因素的回归模型，利用31个地区数据估计出的模型为：

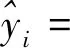
0.194 4xi3

(18)

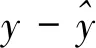
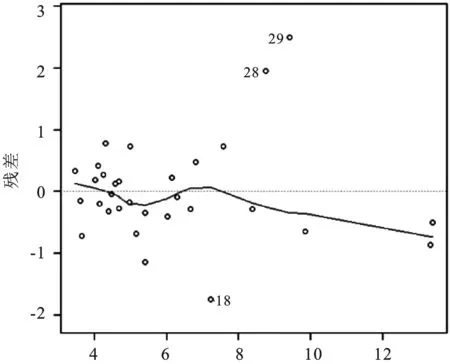
图1a 原模型的残差拟合图

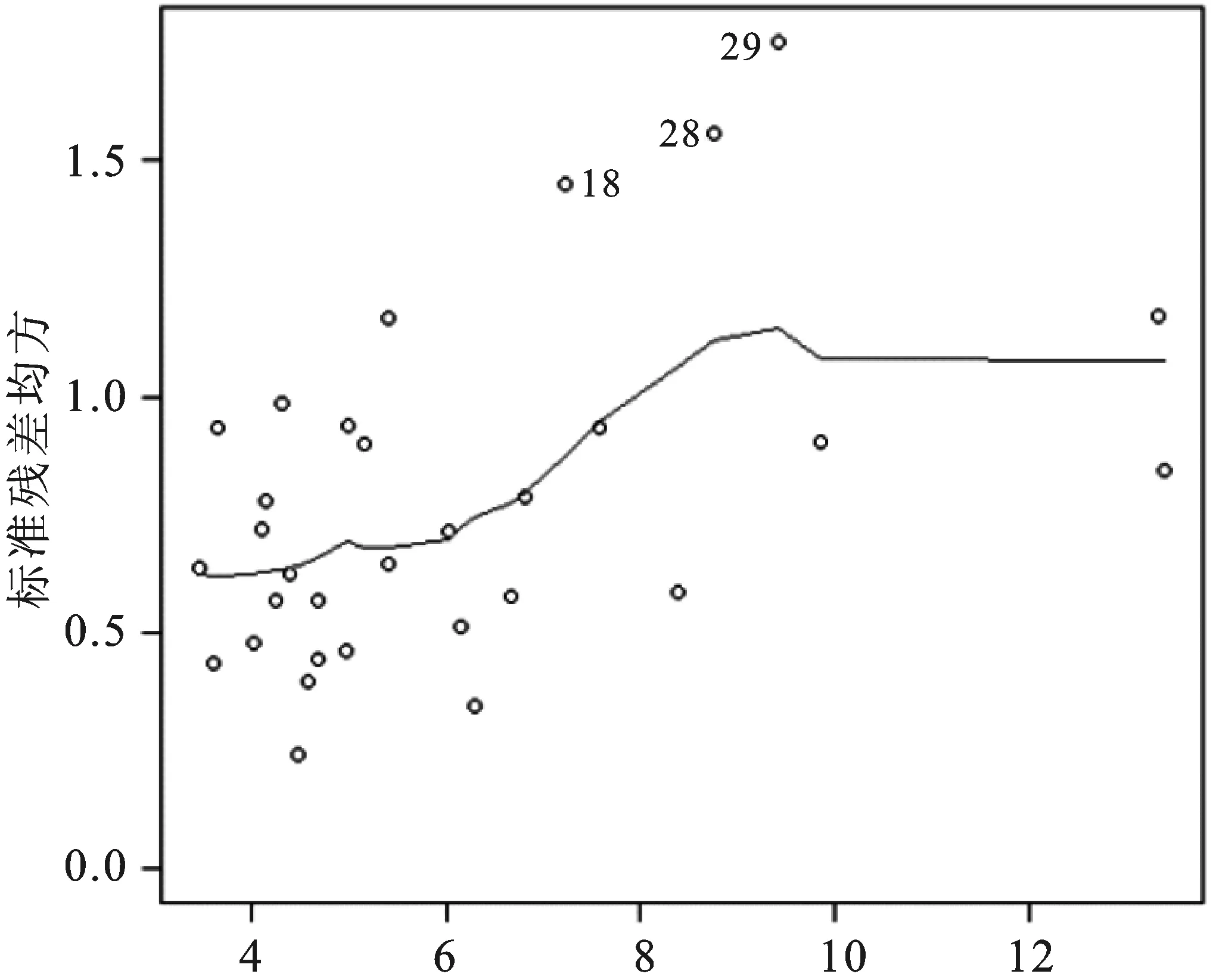
图1b原模型的大小位置图

如图1a和图1b，点的分布都随着拟合值的增大而往外扩散，且残差和标准化残差均方都随着拟合值的增大而增大。这两幅图表明随着拟合值的增大，残差的波动幅度变大，初步判定模型中存在异方差性，下面对该模型分别进行传统的帕克检验和改进的帕克检验。

1.传统的帕克检验。根据(4)式得到3个异方差模型表达式分别为：

(19)

(20)

(21)

(19)～(21)式中lnxi1、lnxi2进行t检验的P值分别为0.008 257、0.012，小于0.05，lnxi3进行t检验的P值为0.853 6，大于0.05，表明原模型存在异方差性，且该异方差与解释变量xi1，xi2有关。

2.改进的帕克检验。根据(9)式得到主成分的表达式为：

(22)

由公式(11)建立异方差模型，得到该异方差结构回归模型表达式为：

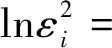
0.043 1ln|zi2|-0.155 9ln|zi3|

(23)

(23)式中ln|zi1|的t检验的P值为0.040 5，小于0.05，ln|zi2|、ln|zi3|的t检验的P值分别为0.878 2、0.587 7，大于0.05，表明原模型存在异方差性，且异方差与第一主成分有关。由(22)式中第一主成分表达式的解释变量前系数的大小，表明第一主成分主要与xi1，xi2有关，继而确定引起异方差的主要解释变量为xi1，xi2。

对比传统的帕克检验方法和改进的帕克检验方法可知，传统的帕克检验通过3个异方差模型得到原模型存在异方差性，而改进的帕克检验只需建立1个异方差模型得到原模型存在异方差性，改进的方法避免了传统帕克检验重复拟合的工作量，并且模型更为简单。同时，改进的帕克检验得到异方差与xi1，xi2有关，这与传统的帕克检验得到的结论一致，说明改进的方法可以代替传统的帕克检验方法。

六、结论

改进的帕克检验方法用全部主成分代替单个解释变量建立异方差模型，消除解释变量间相关性的同时，减少了传统帕克检验在多元线性回归模型中重复拟合的工作量。这不仅继承了传统帕克检验的优点，而且能表达出多元线性回归模型下的异方差具体形式，使建立的异方差模型更为准确简便。模拟数据和实证分析表明，该方法的检验效果良好。目前，对传统帕克检验方法的更进一步的探究极少，此方法是在传统的帕克检验方法基础上对多元线性回归模型进行异方差检验的一次成功改进，但在异方差模型的构造方面还有待进一步研究。