中国PM2.5污染时空趋势研究——基于贝叶斯时空统计视角

李俊明

(山西财经大学 统计学院，山西 太原 030006)

一、引言

随着遥感对地观测技术的飞速发展，积累了大量的遥感数据，其不仅广泛应用于大气、海洋和环境等自然科学领域，而且也逐渐应用于社会、经济等领域。目前关于遥感数据的统计分析研究亟需加强，尤其是遥感数据的时空统计已成为数据科学领域的研究热点，其作为一个新兴研究领域，目前还未形成完善的理论方法体系。

由于在任一时点上的任一空间位置只能实现一次采样，因此，时空样本数据不满足大样本前提。再者，由于时空相关性的广泛存在，也不满足独立同分布前提。综上，时空样本数据同时突破了经典统计要求的两个前提：大样本和独立同分布。贝叶斯统计无须满足大样本前提，同时可将时空相关以先验信息形式融入模型，可以说，贝叶斯统计用于时空数据分析在理论上更严密可靠。贝叶斯时空统计已成为国外前沿研究领域，近年来也受到国内学者重视。现有相关研究多是针对单一数据源场景，大都适用于面状(如行政区划)统计数据样本情境，Li等人在2014年提出一种适用于面状计数数据的贝叶斯时空层次模型，分析了2005—2008年英国彼得伯勒市的入室盗窃风险的时空变化和影响因素[1]；Bennett等人基于区、县级行政区年度人口调查数据，利用贝叶斯时空层次模型分析预测了1981—2030年英国人口预期寿命的时空趋势[2]。基于公共健康面状计数数据，Lawson和Kang等就贝叶斯时空统计在疾病制图方面的应用进行了研究[3-4]。张俊辉、吴北平、夏勇等也都应用贝叶斯时空统计模型分析面状时空数据[5-7]。

还有学者基于遥感数据对中国PM2.5污染的时空统计规律进行了研究。江佳等采用简单平均法和做差法研究了1998—2015年中国PM2.5污染的总体空间格局和局部变化趋势[8]。周亮等以时序罗列形式定性分析了中国PM2.5污染总体空间特征，以县级行政区划为统计单元，采用简单比较法描述分析了2000—2011年中国PM2.5污染每隔三年的变化趋势[9]。Peng等通过对像素单元进行独立的简单线性回归分析了1998—2011年中国PM2.5污染的变化趋势[10]。上述研究以独立的统计单元进行统计分析，并未考虑时空变化过程中的时空相关性和时空耦合效应。本文采用一种基于多尺度嵌套空间统计单元的贝叶斯时空层次模型[11]，首次将其应用于中国PM2.5污染的时空演化研究中，在综合考虑时空相关性和时空耦合效应基础上研究了2000—2014年中国PM2.5污染的时空变化趋势。另外，通过该模型可将贝叶斯时空统计方法引入遥感大数据分析领域，一方面丰富了时空大数据分析方法体系，另一方面也拓宽了遥感大数据分析的广度和深度，可增强对跨学科、多领域交叉问题的解决能力。

二、基于多尺度嵌套空间统计单元的贝叶斯时空层次模型

贝叶斯时空层次模型可将一个复杂的时空变化过程分解为总体空间过程、总体时间过程和时空交互过程，其能够精细、科学地刻画时空演化过程，同时贝叶斯时空层次模型也可以考虑更多不确定性。尽管贝叶斯时空层次模型已得到较为广泛应用，但还未在遥感大数据分析得到广泛应用。贝叶斯统计模型分析遥感大数据时，一方面，要解决计算效率问题，因为贝叶斯统计推断一般由蒙特卡洛马尔可夫链(MCMC)算法实现，其本身计算量就已很大，若再以单个像元为统计单元进行贝叶斯统计推断，计算负担会呈指数级增加；另一方面，时空现象是不同尺度的动态耦合过程，时空变化尺度未知时，应采用多尺度统计单元进行分析[12]。对于遥感大数据时空分析问题，一般是基于固定尺度的单个像元进行统计分析，通常以3×3像元的一阶空间邻接考虑空间相关性，这样并不能反映时空过程中的多尺度耦合效应。基于上述考虑，本文拟采用一种适用于遥感大数据的贝叶斯时空层次模型，该模型的构建可分为两步，第一，构建多尺度嵌套空间统计单元，第二，以嵌套结构形式建构贝叶斯时空层次模型。

(一)构建多尺度嵌套空间统计单元

构建多尺度嵌套空间统计单元的总体思路是：根据遥感时空数据在每个时间截面上的局部变异程度，在研究区域范围内，实施n(n=1，2，3，…)轮递次尺度的均质网格剖分，最终形成多尺度嵌套空间统计单元，每一个空间统计单位格网内的像元属性数据在每一个时间截面上均满足均质条件。多尺度嵌套空间统计单元的构建有两个关键点：一是均质程度测度指标选择，二是格网剖分形式确定。均质程度测度指标采用变异系数：

(1)

其中CV代表变异系数，Std表示标准差，Mean表示均值。变异系数越小，则变异程度越小，统计学上一般认为，当变异系数小于15%时，则可认为样本数据均质；考虑到遥感数据是正方形阵列结构，空间剖分形式采用四叉树正方形剖分形式，如图1所示：

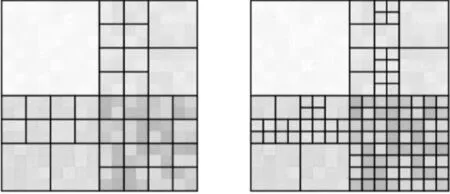
第1级尺度部分 第2级尺度部分第3级尺度部分 第4级尺度部分图1 多尺度嵌套空间统计单元构建示意图

(二)多尺度嵌套空间统计单元的统计性质

(2)

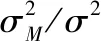
表1 原始遥感数据变异系数CV和剖分阈值λ0不同取值组合条件下取值表

(三)基于多尺度嵌套空间统计单元的贝叶斯时空层次模型

本文采用了本人曾提出的适用于遥感大数据的贝叶斯时空层次模型，该模型以前述构建的多尺度嵌套空间统计单元为基础，以时空局域均质为基准，充分考虑了遥感时空数据的时空局域异质性，突破了以像元为固定尺度的传统分析思路，实现了以多尺度嵌套形式分析时空过程，同时也能显著降低遥感时空大数据分析的计算负担，有效实现对遥感时空大数据的贝叶斯统计分析。该模型以像元属性值为样本观测值，以多尺度嵌套均质空间剖分格网为空间统计单元，通过双层嵌套结构实现贝叶斯时空层次模型构建，包含三个子模型，分别是数据模型、过程模型和参数模型[13]，其对应的数学表达如下：

数据模型为：

(3)

过程模型为：

ln(μM[i]，t)=Φ+SM[i]+ΩM[i]+B0t+νt+

BM[i]t+εM[i]，t

(4)

参数模型为：

(5)

BM[i]～CAR.Gauss(B.adj.sp(M[i])，

(6)

vt～CAR.Gauss(v.adj.tm(t)，

(7)

三、实证研究

(一)研究区域与数据来源

本文基于的遥感数据来源于加拿大达尔豪斯大学van Donkelaar团队在2016年3月发布的最新版全球PM2.5年均浓度遥感数据产品，空间分辨率为0.1°×0.1°[14]。经测算，2000—2014年中国PM2.5年均浓度遥感数据共包含1 444 080(96 272×15)个像元。另外，该PM2.5年均浓度遥感数据与地面站点监测数据具有较好的统计显著一致性(R2=0.81)，数据精度较高，具体可参见相关文献[14]。

(二)多尺度嵌套空间统计单元构建结果

在贝叶斯时空统计分析前，需先构建多尺度嵌套空间统计单元，经计算，2000—2014年中国PM2.5年均浓度遥感数据的变异系数最小值为71%，根据表1可知，为使得以多尺度嵌套空间统计单元计算的方差保持在原始遥感数据方差的0.998以上，剖分阈值λ0确定为4.0%，多尺度级别设定为3级即可满足局部均质条件，三级尺度依次为0.8°×0.8°、0.4°×0.4°和0.2°×0.2°。最后构建完成的嵌套三级多尺度空间统计单元共包含7 072个统计格网单元，其中三级尺度统计单元个数分别为373、4 171和2 528。

(三)贝叶斯时空统计结果

1.总体空间格局。总体空间格局由式(4)中的总体空间相对度系数exp(SM[i])的后验估计测度，具体而言，若exp(SM[i])>1.0，则说明该M[i]统计单元上的PM2.5污染程度是全国PM2.5总体污染程度的exp(SM[i])倍，反之亦然。进一步，还可以根据后验概率P(exp(SM[i])>1.0|y)的大小确定PM2.5污染热点、冷点和温点区域范围。

贝叶斯时空统计结果表明，中国有18.9%的区域PM2.5污染程度高于全国总体水平的2.5倍，全国有10.4%的区域PM2.5污染程度高于全国总体水平的3.0倍，甚至还有6.5%的区域PM2.5污染程度高于全国总体水平的3.5倍。从空间结构而言，中国PM2.5重度污染区域的空间分布呈现出 “两团一带”分布特征，“两团”分别指四川盆地和新疆塔里木盆地区域，而“一带”是指由京津冀南部、山东、江苏、上海和浙江北部为起始，向西南方向延伸，经由河南、安徽、湖北、江西、湖南、广西和广东西部等区域。在这“两团一带”区域中，PM2.5污染最严重的地区(比全国总体水平高3.5倍以上)分布在两个连片区域，一个是华北平原和长三角地区北部及湖北中部，另外一个区域是四川盆地区域，这两个地区人口总量大，人口密度高，根据2010年中国人口分布密度数据统计显示，这两个PM2.5污染最严重区域的暴露人口总量多达4.2亿人，占全国总人口的32.8%。根据exp(SM[i])>1.0的后验概率大小可知，中国PM2.5污染冷点区域(P(exp(SM[i])>1.0|y) <0.2)面积占全国面积的37.3%，对应的暴露总人口占比3.5%，而中国PM2.5污染热点区域(P(exp(SM[i])>1.0|y) >0.8)面积占比为63.3%，对应的暴露总人口占比92.5%。

根据PM2.5污染总体空间相对度系数exp(SM[i])的大小，本文将PM2.5污染程度分为七个级别，对应exp(SM[i])的7个取值范围为：0.2～1.0、1.0～1.5、1.5～2.0、2.0～2.5、2.5～3.0、3.0～3.5、3.5～4.5等，将一级定为轻度污染级，二级定为较轻度污染级，三级和四级定为中度污染，五级定为较重污染级，六级为重度污染级，七级定为严重污染级。表2列出了中国大陆31个省份中对应的七级PM2.5污染区域占本地区总面积百分比统计结果。天津、河北、上海、江苏、安徽、山东和河南等7省份的重度和严重污染区域所占的面积排在31个省份前列，特别是江苏，99.66%的区域PM2.5污染处于最高污染级——严重污染(七级)，北京PM2.5污染等级属于二级(轻度污染级)、三级和四级(中度污染级)等层级。虽然四川盆地和新疆塔里木盆地的PM2.5污染较重，但这两个地区的地域面积较大，因此重度污染和严重度污染的区域面积占比并不是很高。内蒙古、黑龙江、四川、西藏、青海、福建、海南和云南8省的PM2.5轻度污染区域面积占比均超过50%。PM2.5中度污染区域面积占比超过50%的地区有北京、山西、辽宁、浙江、江西、广东、贵州、陕西、甘肃和宁夏10个省份，PM2.5较重度污染区域面积占比超过50%的地区有湖南和广西两个省份。总之，从PM2.5等级污染区域面积占比角度而言，PM2.5一级(轻度)污染为主的省份有5个，PM2.5二级(较轻度)污染为主的省份有3个，PM2.5三、四级(中度)污染为主的省份有10个，PM2.5五级(较重)污染为主的省份有两个，PM2.5六级(重度)污染为主的省份有0个，PM2.5七级(严重)污染为主的省份有6个，其余的河北、吉林、湖北、重庆和新疆5个省份没有出现超过50%面积占比的主导级别污染区域。

表2 2000—2014年中国大陆31个省份内七级PM2.5污染对应的区域面积占比统计表

2.总体变化趋势。2000—2014年，中国PM2.5污染在总体变化趋势方面呈现出一个基本平稳而稍有上升的变化特征，可将其分为两个阶段，即2000—2006年和2006—2014年，前一阶段呈现出强于整个研究期间的增长趋势，虽然后一阶段出现了下降趋势，但由于2006—2014年的下降趋势强度弱于2000—2006年的增长趋势，因此在整个研究期间，中国PM2.5污染仍然呈现出上升趋势。总体变化趋势只是时空变化的一个概括性描述，而局部区域甚至单个的空间统计单元的局部变化趋势却表现出不同于总体变化趋势的特点。

3.局部变化趋势。局部空间区域上的变化趋势即局部变化趋势更能体现出时空变化过程中稳态结构之外的时空变化规律，由式(4)中的局部变化趋势参数BM[i]来描述，既考虑了空间维度上的影响，也考虑了时间过程中的影响，若BM[i]>0，则说明该空间统计单元上的PM2.5污染在2000—2014年具有增加的局部趋势，若BM[i]<0，则说明该空间统计单元上的PM2.5污染在2000—2014年具有降低的局部趋势。

研究表明，在2000—2014年，中国西部区域出现了较强的PM2.5污染加重趋势，主要包括新疆、青海和甘肃北部等地区，且在空间上呈现出连片特征，需要指出的是，西藏中部地区和云南西部地区的PM2.5污染也出现了增加的局部趋势；在一些PM2.5重度污染程度地区，也出现了局部增加趋势，这些区域在空间上形成了“X”型的分布结构特征，主要由陕西南部、湖北、河南、长三角地区北部、山东、京津冀地区及其北部等区域构成，黑龙江中部、东部沿海区域、吉林北部和中部区域的PM2.5污染也出现了一定程度的局部加重趋势。另外，PM2.5污染较重的四川盆地呈现出下降的局部趋势，而且位于中国东南区位的广西、湖南、广东、江西、福建、台湾以及浙江等省份，在PM2.5污染变化趋势方面也呈现出局部下降的态势，且以台湾、福建、浙江南部、江西南部、广东东部等区域的局部趋势下降趋势最明显。

进一步分析可知，全国有41.4%的区域局部变化趋势系数BM[i]>0的后验概率大于0.80，也就是说全国有41.4%的区域PM2.5污染在2000—2014年以大于80%的概率加重，而有35.6%的区域局部变化趋势系数BM[i]>0的后验概率小于0.20，即这些区域的PM2.5污染在2000—2014年具有一定的下降趋势，其余23.0%的区域局部变化趋势系数BM[i]>0的后验概率在0.20到0.80之间，说明这些区域在2000—2014年并没有呈现出显著的局部变化趋势，具有不确定性。

(四)与其他研究对比

在经典统计中，简单平均法最为常用，而贝叶斯时空统计模型估计的总体空间格局与简单平均法计算的空间格局具有明显差异，简单平均法容易受异常值的影响，而且也未考虑时空变化过程中的耦合效应，因此简单平均法计算的空间格局一定会混杂稳态和非稳态两种格局，并不能清晰地刻画出时空变化规律。时空分析中常用的另外一种方法是经验正交函数法(EOF)，但EOF时空分析方法没有清晰的机理解释结构，对其结果需要根据不同问题结合专业知识进行解释。本文也利用EOF法统计分析了2000—2014年中国PM2.5污染，结果显示，经过EOF计算后的第一模态和第二模态已经分别解释了90.8%和5.7%的时空变化，进一步研究可知，EOF计算的第一模态空间格局与简单平均计算的空间格局基本一致，而第二模态结果却找不到明晰的机理解释。贝叶斯时空统计模型兼具贝叶斯统计和时空交互模型优点，可以综合考虑时空过程中的耦合效应，并具有清晰的机理解释结构，对估计结果可以给出清晰的时空变化过程机理解释，同时，还具有较强的可扩展潜力。另外，贝叶斯时空统计模型遵从贝叶斯统计范式，因此可以考虑更多不确定性，并对异常值具有一定免疫性能，进一步增强了对复杂变化过程的分析刻画能力。

综上所述，虽然一些学者利用经典统计方法也研究了中国PM2.5污染的时空变化，但未很好地考虑时空相关性和时空耦合效应。Li等曾采用贝叶斯时空层次模型研究了1998—2014年中国PM2.5污染的时空变化特征[1，15]。Li等的研究是直接将已有的贝叶斯时空层次模型移植应用到遥感数据分析中，先将遥感数据平均化处理到中国县级行政区划中，然后再以平均化处理后的县级行政区划面状数据进行统计分析，这种处理方法会大大降低遥感数据原有的高分辨率优势和数据精度。本文采用的是基于嵌套多尺度空间统计单元的贝叶斯时空层次模型，保持了遥感数据的原有精度，不仅保持了统计结果的可靠性，而且也能得到较为精细的统计结果。此外，本论文还对贝叶斯统计结果进行了深入、系统的分析，对国家相关政策制定具有一定参考意义。

四、主要结论及建议

本文首次将基于多尺度嵌套空间统计单元的贝叶斯时空层次模型应用于2000—2014年中国PM2.5污染时空演化研究中，并拓展了嵌套多尺度空间统计单元构建参数λ0的适用范围。本研究认为，基于多尺度嵌套空间统计单元的贝叶斯时空层次模型不仅有效提高了模型计算效能，而且能在一定程度上反映时空过程中的多尺度耦合效应。

研究发现，第一，2000—2014年，中国PM2.5污染已经形成了稳定的“两团一带”空间结构；第二，中国PM2.5重度污染区域主要由三个地区构成：华北平原和长三角地区、四川盆地和新疆塔里木盆地；第三，PM2.5污染程度较低区域虽然占全国总面积比例为37.3%，但这些区域内所居住的总人口只占全国总人口的3.5%，PM2.5污染高于全国总体水平的区域占全国总面积的63.3%，但对应暴露人口占比却高达92.5%；第四，2000—2014年，PM2.5轻度污染的西部区域出现了较强的局部加重趋势，而且陕西南部、湖北、河南、长三角地区北部、山东、京津冀地区及其北部等PM2.5重度污染区域也呈现出局部增加趋势，并在空间上形成了“X”型空间结构；第五，PM2.5污染较重的四川盆地呈现出下降的局部趋势，同时位于中国东南区位的广西、湖南、广东、江西、福建、台湾以及浙江等地区也呈现出下降的局部变化趋势，且以台湾、福建、浙江南部、江西南部、广东东部等区域的局部趋势下降最为明显。

建议国家相关部门在制定空气污染防治政策时，不仅要关注当前的PM2.5污染空间格局，更要综合考虑全国各个地区PM2.5污染的局部变化趋势，尽管重度污染地区亟待重点治理，但具有局部加重趋势的轻度污染西部地区也应成为重点防控地区。可根据PM2.5污染的不同等级、局部变化趋势以及暴露人口密集程度划分出不同等级的防控区域，并制定阶梯性防控政策和措施体系。另外，PM2.5污染不是区域独立性现象，而是全域甚至全球性问题，在制定大气污染防治措施时，要重视区域内部及与周边区域的交互影响，应不断加强区域间甚至国家间的联防联控与合作治理。