基于圆形绕制线圈建模的设计与优化

陈佳男， 秦会斌

(杭州电子科技大学 新型电子器件与应用研究所，浙江 杭州 310018)

0 引 言

本文将基于圆形绕制线圈(wound coil)的耦合系数，对线圈半径进行优化，目前在该领域中，即使采用单圈线圈的简单情况，仍没有得到最优半径选择方法的解析解，在缺乏理论指导的情况下，往往通过多次仿真或实验的方法得到发送接收线圈最优半径[1]。本文针对可穿戴设备及植入式医疗电子器件的无线供电应用，拟通过对线圈的电阻电感电容(resistance inductance capacitance,RIC)进行解析建模，通过公式推导得到以最大化传输效率为目标的最优半径的解析解，并经ANSYS HFSS仿真验证。

1 系统及线圈建模

二线圈电感耦合无线供电系统模型如图1所示，图中的VS为等效的系统供电电源，RS为电源内阻；R1和R2分别为发送线圈和接收线圈寄生电阻，C1和C2分别为发送线圈接收线圈的寄生电容，RL为负载内阻。L1和L2分别为发送线圈接收线圈自感，MC1为两线圈之间的互感值。发送端串联电容CC1用于提高系统电源VS的功率因素。

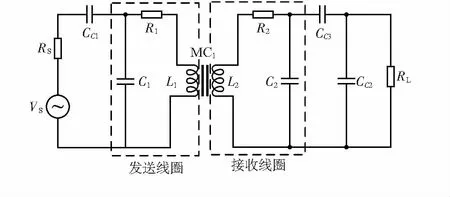
图1 二线圈电感耦合无线供电系统模型

在系统接收端加入阻抗匹配网络可以将负载变换到最优的负载值ZL(opt)，并最大化系统能量传输效率。接收端的阻抗匹配电路由电容CC2和CC3实现，此时系统的最优传输效率ηmax和对应的负载阻抗ZL(opt)如式(1)所示。其中k,Q1和Q2分别为线圈间的耦合系数、发送线圈品质因数和接收线圈品质因数，ω为工作频率。耦合系数和品质因素可计算如下[2]

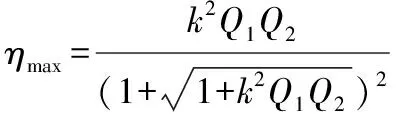
(1)

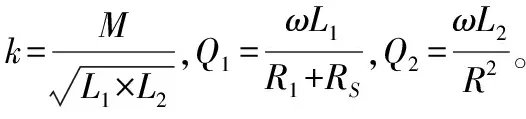
图1中的电容CC2，CC3和负载电阻RL组成的局部电路的阻抗值应该等于最优负载,即满足关系

(2)

通过对式(1)、式(2)求解得到阻抗匹配网络所用的两个电容取值，可用式(3)表示

《议定书》推动中国—东盟自由贸易区升级发展。但是，《议定书》并未涉足TPP开创和引领的多个“边境后”规则，并未改变中国—东盟自由贸易区以边境规则为主，属于传统关税治理协议范畴的属性。事实上，我国建立中国(上海)自由贸易试验区的初衷之一，就是顺势利用全球经贸规则新高地TPP带来的倒逼改革效应，在国内建设能够对标TPP高标准、高要求的新开放高地。而且，中国—东盟自由贸易区在关税领域的改进空间非常有限，升级版建设应该以更高的开放水平为目标，尝试性、试验性、渐进性推动更大领域的双边市场开放与管制对接。

(3)

在发送端，电容CC1可以通过与电感L1形成串联谐振实现阻抗匹配，提高电源端的功率因素。因此CC1可以根据工作频率ω来确定

(4)

1.1 自感、互感、耦合系数模型

对于线圈半径为a，导线的线半径为r的单圈圆形线圈，当a/r≪1时其自感可表示为[3]

(5)

对不同半径下的二线圈结构，可用如下互感近似计算表达式[4]

(6)

式中 两线圈半径分别为a和b，发送接收线圈距离为z，γ=2ab(a2+b2+z2)。

1.2 线圈寄生电阻

线圈中的寄生电阻受趋肤效应与邻近效应的影响，由于本文选用单匝圆形横截面的线圈，故邻近效应可忽略不计。根据文献[5]，一个横截面为圆形的无限长直导线趋肤效应电阻为

(7)

式中lw和σ分别为线的长度和电导率，Rdc为直流电阻，μ0和μr分别为真空中铜的磁导率和环境中的相对磁导率，ber(m)，bei(m)，ber′(m)和bei′(m)均为开尔文函数。当导线线半径远小于所围线圈的直径时，线圈可以被近似当成直导线来计算其趋肤效应电阻[6]。

2 系统优化过程

在对系统建模时发送线圈拟采用美国线规(American Wire Gauge)AWG18，接收线圈采用AWG36规格的铜线。一般来说，在可穿戴设备以及植入式医疗器件的应用中，发送接收线圈尺寸及能量传输距离通常由具体应用确定[7，8]。在这里，假设接收线圈半径固定。目标为在任何传输距离的情况下，确定最佳的发送线圈半径以最大化无线电能传输效率。

由效率表达式(1)可知，在接收发送品质因素Q1，Q2固定时，系统效率与线圈之间的耦合系数k单调递增。收发线圈品质因素Q1，Q2常常与线圈材质、线的粗细程度相关。本章节不做讨论。在这里假设线圈半径≫导线的线半径，接收线圈半径a，发送线圈半径b，根据k=|M|/(L1×L2)2，将式(5)、式(6)代入，得到耦合系数k表达式(8)

(8)

式中 常数λ=π/(ln(C2/ρ)+c4ρ2)。

对耦合系数k(b)求导。存在两个极点，b=0，或b2=a2+z2。即当发送线圈半径满足式(9)时，耦合系数最大，此时的耦合系数最大值如式(10)所示

b=a2+z2

(9)

(10)

3 理论验证与仿真

3.1 曲线拟合验证

上面通过对线圈之间耦合系数的优化可知，在任意距离下，接收线圈半径固定时，发送线圈半径满足b=(a2+z2)1/2，收发线圈之间有最大的耦合系数。可以通过对耦合系数的优化，得到最优的系统能量传输效率。

目前，可穿戴设备线圈尺寸通常在cm级别[9]，系统一般工作在为兆赫兹(MHz)频率段[10]。假设接收线圈半径为20 mm，系统能量传输距离在5～100 mm的变化范围内，对不同发送线圈半径进行扫描，得到不同距离下，发送线圈半径与系统效率的关系如图2所示。

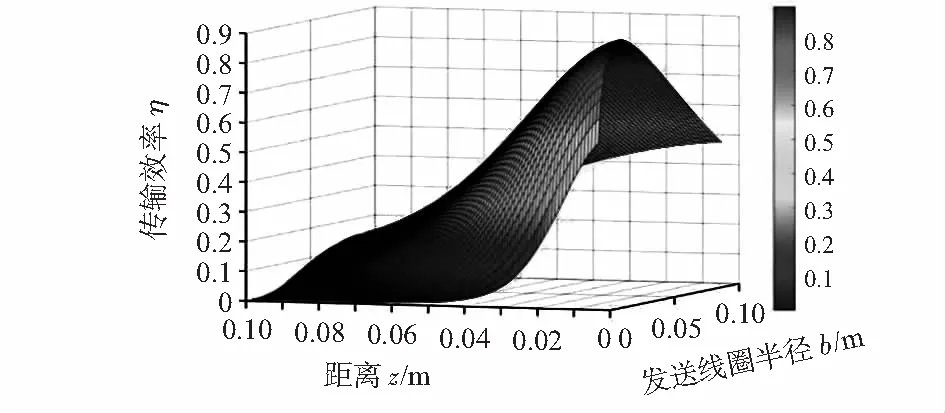
图2 传输效率与发送线圈半径、传输距离之间的关系

观察图2曲线可知，在该模型下，当接收线圈尺寸固定，图中系统在每一个传输距离z下均存在一个最优的发送线圈半径b，能够最大化传输效率η。为了得到每一个最优传输效率下的接收线圈半径a、发送线圈半径b以及传输距离z三者之间的关系。利用MATLAB软件，本文通过2000余组数据对这三者的关系进行曲线拟合。

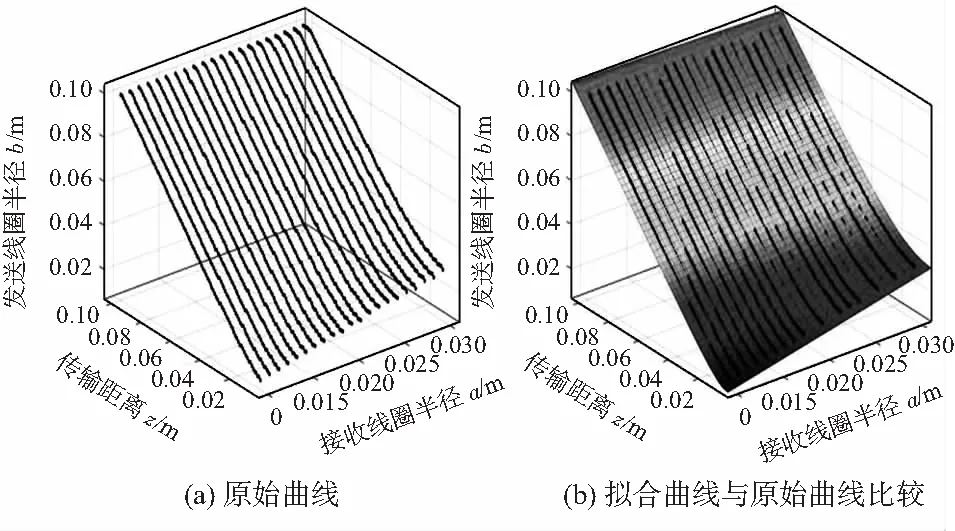
图3 曲线拟合结果

通过以上拟合结果发现，即当接收线圈半径固定时，任意距离下均存在最优发送线圈半径使得系统达到最优能量传输效率，与此同时，接收线圈半径a，传输距离z与最优发送线圈半径bopt三者之间的关系如式(11)所示

(11)

3.2 仿真验证

对上述得到的最优发送线圈半径选择的结论，本文选取了两个例子在电磁场仿真工具Ansoft HFSS中进行验证。在HFSS中的仿真模型设置如图4所示。

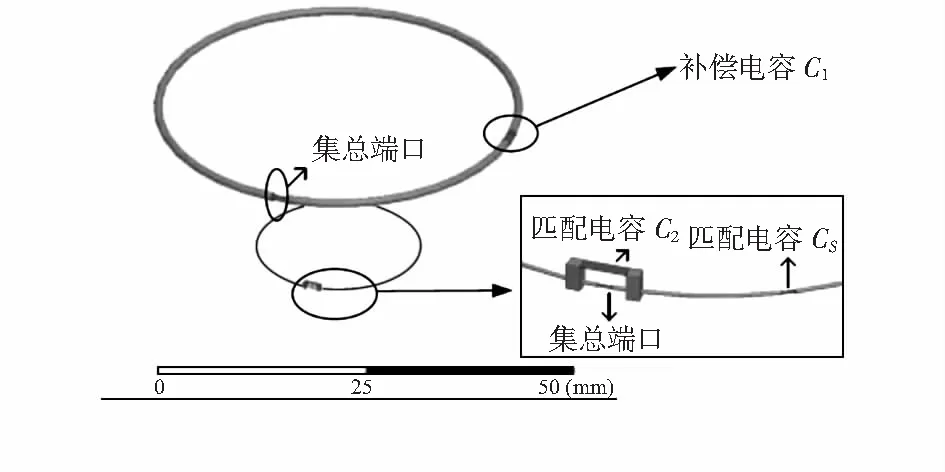
图4 HFSS中接收线圈半径20 mm、距离20 mm的模型设置

其中接收线圈半径为20 mm，传输距离为20 mm，发送线圈半径在5～100 mm之间进行频率扫描，扫描范围1～100 MHz。设定系统需要工作在13.56 MHz下的ISM频段，在发送线圈半径不断改变而导致自身谐振频率不断变化的情况下，通过改变发送线圈补偿电容CC1的值进而控制线圈的强迫谐振频率来保证该系统工作在谐振状态下。另外在接收线圈部分通过电容CC2和CC3来进行系统的阻抗匹配。其中CC2和CC3的值可根据式(3)计算得到。在HFSS中这些电容通过设置“Lumped RLC”设置得到。在这些电容的补偿下，可实现系统的阻抗匹配并使传输效率分别达到对应线圈半径设置下的最大值。图5比较了不同发送线圈半径下的能量传输效率HFSS仿真和理论推导结果。

图5 传输效率与发送线圈半径b的关系

从图5中可见，系统能量传输效率的仿真结果和理论推导结果比较接近(约5 %的误差)，仿真结果中系统达到最优效率时对应的发送线圈半径为22 mm，与第2节中的结论b=(a2+z2)0.5吻合。

图5(a)证明了当发送线圈半径与传输距离较为接近时，第2节中的结论是正确的。图5(b)则比较当接收线圈半径(20 mm)小于传输距离(50 mm)时，电磁仿真软件仿真结果与理论推导得到的系统能量传输效率结果比较。从图中可知，仿真结果与理论推导得到的效率值相比较大约也存在5 %的误差，但是它们的最优效率下对应的发送线圈半径一致。均为51 mm，这一现象同样验证了第2节中最优发送线圈半径选择法的有效性。

4 结 论

本文针对磁耦合谐振无线电能传输在可穿戴设备及植入式医疗设备中的应用，研究了最大化能量传输效率与最优发送线圈尺寸的解析解。基于单匝圆形绕制线圈间的解析建模，配合阻抗匹配电路可以计算出线圈间所能达到的最高效率。通过对发送线圈与接收线圈之间耦合系数进行理论推导，得到了最优发送线圈的解析解。计算所得能量传输效率和最优发送线圈的解析解与曲线拟合结果、电磁仿真工具得到的结果吻合。