MEMS谐振陀螺实时自动模态匹配控制技术*

陈 婷, 刘玉县, 吴康雄, 何春华, 汤 丽

(1.长沙理工大学,湖南 长沙 410002；2.北京大学 微纳加工国家重点实验室，北京 100871；3.广东顺德创新设计研究院，广东 佛山 528311)

0 引 言

模态匹配控制技术已经广泛应用在微机械振动陀螺仪来提高检测模态的机械灵敏度以改善其性能[1～4]。由于制造的差异，通过结构设计很难把两种模态的谐振频率完全匹配，因此静电调频方法通常被用来进行模态匹配，在压模梳齿上对调频电压扫描，得到最大输出信号时所对应的匹配电压[5～7]。尽管这种方法很简单，但只适用于高Q值陀螺、匹配精度和匹配时间的折中，另一种比较常见的模态匹配方法是锁相环(phase-locked loop,PLL)控制法[8～10]，该方法的实质是用PLL对驱动信号与检测信号进行锁相，使两者的相差保持在模态匹配情况下的数值，由于多钟耦合信号存在，使得总的耦合信号和科里奥利力以及驱动信号不正交且不同相，很容易干扰匹配控制的准确性，以上两种模态匹配的方法都属于一次性匹配方法，难以实现实时匹配控制。

驱动模态和检测模态谐振频率通常随不同温度而变化，而谐振频率发生变化则增大模态匹配的难度，这使得开发一种自动实时模式匹配控制方法来抑制温度敏感性及其重要，本文提出一种温度-30～60 ℃环境下进行模态自动匹配的实现方法，利用该温度范围内谐振频差与调谐电压对应的函数关系，实时进行模态匹配控制，克服了目前常见模态匹配方法的局限性。

1 微机械陀螺谐振原理分析

本实验采用北京大学Z轴双解耦电容式音叉陀螺，线性谐振陀螺具有驱动和检测两个模态，两个模态与输入角速度方向相互正交以满足在检测模态产生科里奥利加速度的条件，微机械陀螺采用的是谐振的原理，驱动模块使得质量块在静电驱动力的作用下在X方向上保持恒定幅度谐振，当系统以一定角速度绕Z方向进行定轴转动时，质量块在Y方向产生科里奥利加速度，在检测模态下检测质量块在Y方向的位移从而检测转动角速度。

在不考虑其他耦合信号的影响下，振动式MEMS陀螺两个模态下的简化动力学方程如下[11]

(1)

(2)

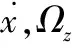
对驱动模态上的动力学方程(1)进行变换可得到系统驱动模态的振幅与相位响应

x(t)=Axsin(ωt+φx)

(3)

(4)

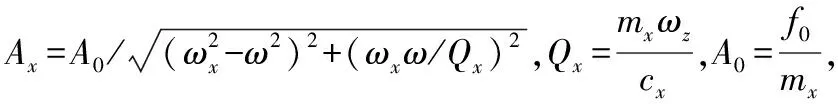
微机械陀螺的开环检测原理框图如图1所示。

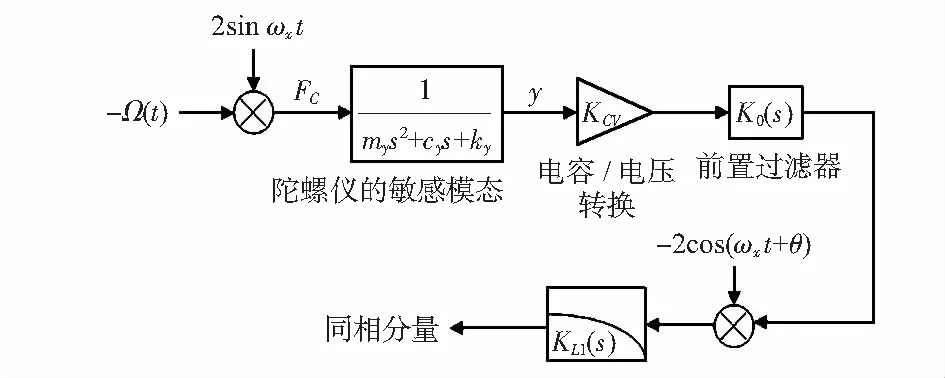
图1 开环检测原理框图

输入角速度-Ω(t)=-ΩRcosωRt被驱动模态的谐振质量块的运动调制后形成科里奥利力作用在检测模态上，检测模态位移信号经过电容电压转换电路后进入前置滤波器进行降噪整形。整形后信号通过-2cos(ωxt+θ)解调滤波得到陀螺的检测模态的响应

y(t)=Ay+sin((ωx+ωR)t+φy+)+

Ay-sin((ωx-ωR)t+φy-)

(5)

式中

定义陀螺的机械灵敏度[12]为

(6)

由于真空封装，Qy值一般比较大，根据式(6)可以得出机械灵敏度达到最大时有ωx=ωy，这时相移φy≈90°， 当模态匹配时(即ωx=ωy)时，检测端响应位移和机械灵敏度分别为

(7)

(8)

式中Fcm=2myΩRAx0ωx，由式(6)可知，微机械陀螺的灵敏度与驱动速度幅值、检测质量、驱动和检测模态的固有频率和检测Q值等因素有关，当模态匹配和检测Q值增大时，机械灵敏度最高，如式(8)。

2 温度敏感性分析

硅材料是一种热敏材料，温度变化不仅会使机械陀螺的品质因子和谐振频率都发生变化，而且对整个硬件电路器件的影响会改变控制系统的零偏输出，影响到陀螺的输出精度和性能。

除了外界环境温度对陀螺性能的影响，陀螺在工作过程中，由于自身特定的结构，陀螺的内部温度也会发生改变，此时陀螺的弹性模量、残余应力等性能受温度影响较大[13]，继而导致陀螺的品质因子发生变化，如图2(a)所示是陀螺驱动模态和检测模态Q因子与温度之间的关系，随着温度从最低温度到最高温度，微机械陀螺的驱动模态Q因子(Qx)和检测模态Q因子(Qy)大约减小到原来的一半，根据之前的分析，驱动模态中，为了维持恒定的驱动振幅，高温时施加的驱动电压要比低温时的高，检测模态中，高温情况会使陀螺的机械灵敏性下降。

微机械陀螺的硅材料的弹性模量随环境温度而发生变化[14]，这使得陀螺的谐振频率也发生变化，图2(b)是陀螺驱动模态和检测模态谐振频率与温度之间的关系图，随着温度的上升，驱动模态与检测模态的谐振频率近似线性减小。

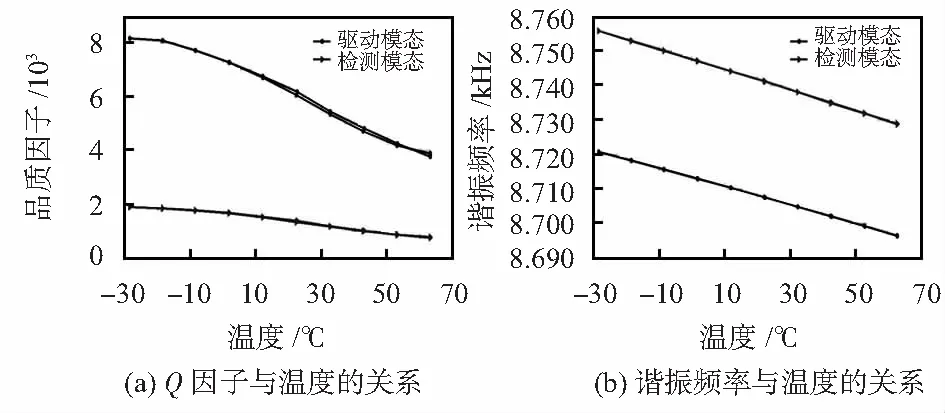
图2 驱动模态和检测模态的Q因子及谐振频率与温度的关系

只考虑硅材料杨氏模量KET带来的影响，驱动谐振频率和检测谐振频率随温度变化表达式为[12]

(9)

(10)

式中fx0和fy0分别为驱动和检测模态室温下的谐振频率，T0为室温，因为KET(T-T0)通常远小于1，所以,对式(9)和式(10)进行泰勒展开最终可以得到

fx(T)≈fx0[1-KET(T-T0)/2]

(11)

fy(T)≈fy0[1-KET(T-T0)/2]

(12)

fx和fy都随温度T线性变化,根据式(12)与式(13)可推出两轴频差Δf随温度变化的表达式

(13)

可见两轴频差Δf随温度变化线性变化。

3 模态匹配控制原理

由于工艺加工存在偏差，陀螺加工后所得到的驱动谐振频率和检测谐振频率并不相等，两者之间会存在一个偏差。但为了获取最大的机械灵敏度，要求微机械陀螺的驱动模态与检测模态都工作在谐振频率处，即fx=fy，图3(a)和图3(b)分别表示非模态匹配和模态匹配陀螺的工作频率与相应关系。

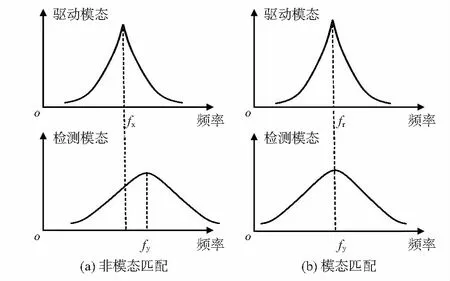
图3 非模态匹配和模态匹配下的幅频响应

MEMS陀螺通常采用压膜模态匹配梳齿结构来实现自动模态匹配控制，在陀螺压膜梳齿上适合将驱动力对位移求导产生静电力负刚度，其表达式为[12]

(14)

式中Vp为压膜梳齿上的直流调频电压，N为检测梳齿数，h和l分别是两个梳齿重合部分的长度和宽度，d1和d2分别是上下梳齿间的距离，而对于已经封装好的陀螺，其结构参数都是固定的，故静电力负刚度ky只跟电压有关，my为检测质量，fx和fy分别为驱动与检测模态的谐振频率，故静电力负刚度发生变化，谐振频率也会变化，调谐电压Vp与检测梳齿的谐振频率fy之间的关系式为[15]

(15)

其结构参数h,l,d1,d2和my通常是固定的，主要通过调节Vp来调节模态谐振频率。

从上述温度敏感性分析中可知，驱动谐振频率fx、检测谐振频率fy和频差Δf与温度之间存在线性关系，进一步简化表示为

fx=kxT+bx

(16)

Fy=ky1T+by

(17)

Δf=fy-fx=(ky1-kx)T+by-bx

(18)

因为fx和fy随温度线性变化，频差也随温度T线性变化，故可以推出在全温情况下Δf与fx之间的函数关系，其表达式为

(19)

根据检测轴谐振频率fy与温度T之间的Vp关系和检测轴谐振频率fy随直流调频电压Vp变化的关系，故可以间接拟合得到全温情况下直流调频电压与检测轴谐振频率之间的实时对应关系。

4 实验结果与分析

根据驱动谐振频率和检测谐振频率与温度存在的关系，通过多次实验获得两模态谐振频率随着温度的变化关系曲线，描绘出检测模态与驱动模态之间的谐振频率的频差与温度的关系曲线，如图4(a)所示，在温度-30～60 ℃范围，两模态的谐振频差Δf变化不超过3 Hz。因温度和驱动模态谐振频率呈线性关系，因此可以以驱动谐振频率位温度参考，经换算得到频差Δf与驱动谐振频率fx之间的关系，如图4(b)所示，Δf与fx近似线性关系。

图4 检测模态和驱动模态间谐振频差与温度、驱动谐振频率的关系

图5(a)给出了实验实测陀螺检测模态谐振频率fy与调谐电压Vp之间的关系。通过多次实验可获得调节频差与调谐电压Vp的关系曲线图，如图5(b)所示。

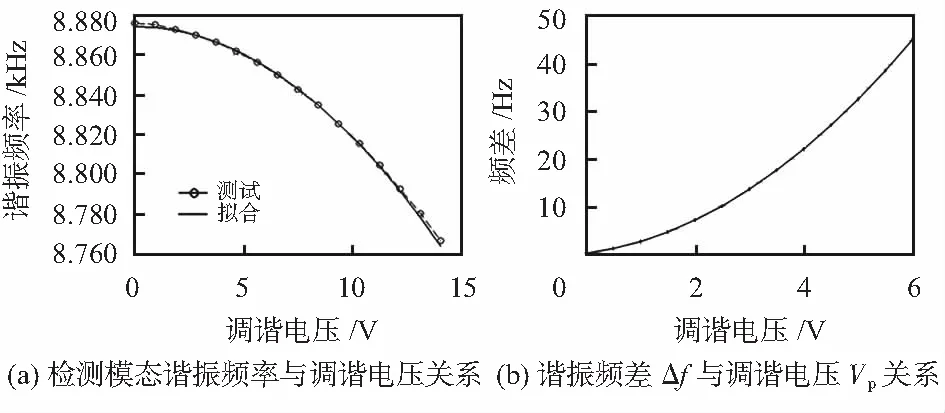
图5 陀螺检测模态谐振频率、调节频差与调谐电压关系

根据图4(b)以驱动频率为参考，实时获得两个模态的谐振频差，通过图5(b)谐振频差与调谐电压关系，实时控制调谐电压，使得检测模态谐振频率和驱动模态谐振频率匹配。对MEMS陀螺进行实时自动模态匹配控制后，在温度-30～60 ℃范围内对系统进行扫频得到匹配后两个模态谐振频率，如图6所示,该温度范围内的匹配误差如图7所示。

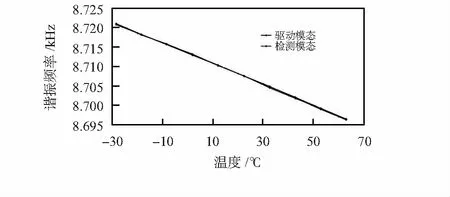
图6 匹配后驱动谐振频率和检测谐振频率与温度关系

图7 模态匹配误差曲线

图6与图7实验曲线是采用间接拟合的方法获得的，进行模态匹配后驱动谐振频率与检测谐振频率匹配误差不超过0.3 Hz。

5 结 论

本文提出一种简单、稳定可靠、快速的自动实时模态匹配方法，实验结果表明:应用所提方法进行模态自动匹配后，两模态的谐振频率在温度-30～60 ℃范围内匹配误差在0.3 Hz以内，从而验证了该方法实时匹配速度、匹配精度和该方法的可行性。