二维细长柱体气动力特性试验研究

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.中冶京诚工程技术有限公司(秦皇岛)，河北 秦皇岛 066004；3.石家庄铁道大学 大型结构健康诊断与控制研究所，河北 石家庄 050043；4.河北省大型结构健康诊断与控制重点实验室，河北 石家庄 050043)

0 引言

在实际工程中，圆柱体构件与正多边形柱体构件因其结构形式简单，受力性能良好而应用广泛，如斜拉桥的斜拉索、悬索桥与拱桥的吊杆、桥墩和桥塔、索膜结构的拉索及吊杆、以及各种建筑和塔桅结构中的细长杆件等。在基本风速较大的区域，这些构件所受风荷载对结构整体的影响不容忽视，如大跨度斜拉桥的斜拉索承受的风荷载对主梁位移和内力的贡献，占全桥风荷载的60%～70%[1]。此外，圆柱体与正多边形柱体构件多以细长杆件形式出现在实际工程中，属于风敏感结构，其风致振动问题比较突出，比如斜拉索的驰振问题[2]、悬索桥和拱桥吊杆的风致共振问题[3-4]。因此，研究圆柱体以及正多边形柱体的气动力特性，对于进行结构的风荷载计算，以及进行振动分析和稳定性检算是非常必要的。

刘庆宽等[5]研究了雷诺数对圆柱气动力和流场特性的影响，研究表明在不同雷诺数分区，气动力和流场特性呈现出不同规律。王汉封等[6]对长细比为5的三维悬臂正方形柱体气动力特性进行了研究，结果表明三维方形棱柱时均阻力系数与升力系数根方差值都明显小于二维方柱的对应值，且三维方形棱柱的涡脱频率也相对较低。王新荣等[7-8]分别对5种不同宽厚比截面和截面宽厚比为2∶1且4种不同圆角率的二维柱体气动力系数的雷诺数效应进行了研究，认为宽厚比2≤B/D≤4的二维矩形截面柱体的气动特性受雷诺数的影响，且随着截面宽厚比的增大，二维矩形截面柱体模型的气动特性对雷诺数越来越敏感；随着圆角率的增大，模型的平均阻力系数减小，且平均阻力系数对雷诺数越来越敏感。目前对于圆柱表面粗糙度对其气动力特性影响的研究相对较少，而对于方柱研究多集中于矩形柱体和正方形柱体，对于正多边形柱体气动力特性研究也相对较少。故本研究对具有5种不同表面粗糙度的圆柱体和4种正多边形(12、16、20、24)柱体进行风洞测力试验，分析了圆柱气动力系数与雷诺数和表面粗糙度的关系，分析了雷诺数、风攻角以及断面边数对正多边形柱体气动力的影响，可以作为工程设计的参考和相关研究的基础。

1 风洞试验

1.1 试验设备

本研究的试验在石家庄铁道大学风工程研究中心的STU-1风洞的高速试验段内进行。高速试验段宽2.2 m，高2 m，长5 m，最大风速为80 m/s，风速从0～80 m/s连续可调，模型区在40 m/s和65 m/s时的湍流度不大于0.16%[9]。

模型的气动力通过安装在柱体模型两端的美国ATI公司生产的DELTA系六分量高频天平测量。模型阻力和升力方向上的量程均为330 N，满量程精度为1/16 N，频率为1 500 Hz。

来流风速由澳大利亚TFI公司生产的眼镜蛇三维脉动风速仪测试，风速测量范围为2～65 m/s，风速测量精度为± 0.5 m/s，响应频率为2 000 Hz。

1.2 模型参数

柱体模型安装如图1所示，柱体模型由有机玻璃管制成，中间贯穿钢管，固定在风洞两侧洞壁外的高频测力天平上。模型水平安装，与来流垂直。模型长度为2 000 mm，直径(圆形)或外径(正多边形)为100 mm，两端分别安装了补偿模型，并安装了5倍模型直径的端板。通过补偿模型避开了风洞两侧的洞壁形成的边界层，保证受力部分处于均匀的流场中；通过端板保证了模型受力部分流场的二维流动，有效消除了模型的端部效应。

图1 模型安装示意图

通过在光滑圆柱体模型表面粘贴细砂或突起物来得到5种不同的表面粗糙度进行风洞试验，研究表面粗糙度对圆柱体气动力特性的影响。5种表面粗糙度分别为0%(表面光滑)、0.3%、0.6%、1.0%、2.5%，具体定义如表1所示。

表1 粗糙度定义

此外，对4种正多边形(12、16、20、24)柱体进行了多个风攻角的测力试验，研究正多边形柱体的气动力特性。由于正多边形具有多个对称轴，风攻角仅在相邻对称轴夹角范围之内取值，故试验中各正多边形柱体模型风攻角工况互不相同，各模型风攻角工况如表2所示。风攻角以模型某一尖角处为0°，模型顺时针(从模型右端面看)转动为正，以正12边形柱体模型为例，风攻角定义如图2所示。

图2 风攻角示意图

正多边形柱体模型风攻角/ (°)正12边形柱体0、3、6、9、12、15正16边形柱体0、3、6、9、11.25正20边形柱体0、3、6、9正24边形柱体0、2、4、6、7.5

2 试验结果分析

2.1 气动力系数

气动力系数包括阻力系数、升力系数和扭矩系数，其中阻力系数和升力系数[10]按照式(1)、式(2)定义

(1)

(2)

式中，U为上游来流平均风速；CD、CL分别为模型的平均阻力系数与平均升力系数；FD、FL分别为模型的平均阻力与平均升力；L为模型的长度；B为模型特征宽度(此处为直径)；ρ为风洞内空气密度。

2.2 圆柱体气动力特性分析

对不同表面粗糙度的圆柱体模型进行风洞测力试验，得到各圆柱体模型的平均阻力系数和平均升力系数随雷诺数的变化曲线如图3～图4所示。

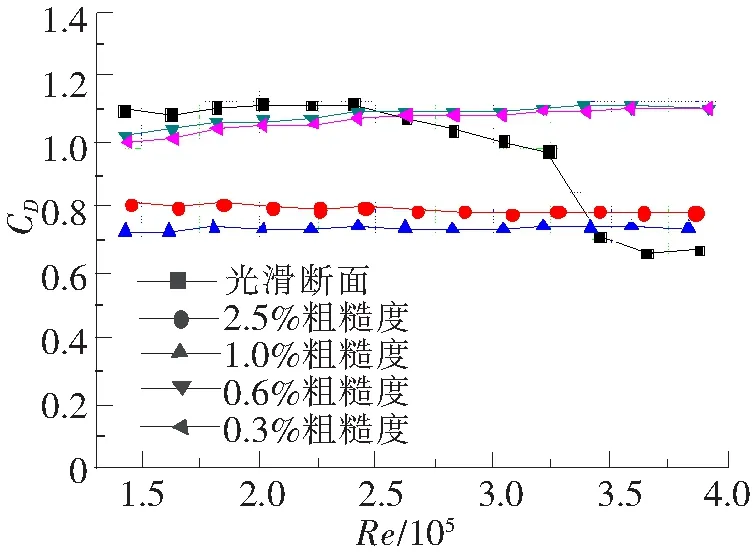
图3 平均阻力系数随雷诺数变化

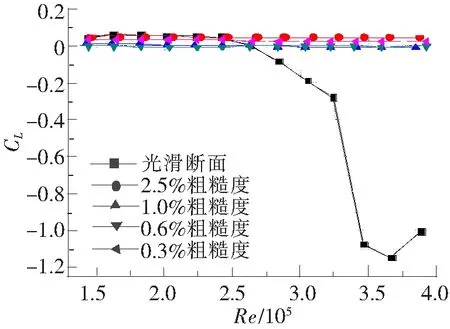
图4 平均升力系数随雷诺数变化

由图3可以看出，光滑表面的圆柱体的平均阻力系数受雷诺数影响较大，从雷诺数为25万左右开始下降，进入临界区，在雷诺数为36万左右降至最低点约为0.66，当雷诺数增至38万时阻力系数又开始有上升的趋势。而粗糙表面的圆柱体平均阻力系数受雷诺数影响较小，变化曲线平缓，并且不同表面粗糙度圆柱体的阻力系数差别较大：0.3%和0.6%表面粗糙度的阻力系数比较接近，在试验雷诺数范围内，阻力系数基本都大于1.0；1.0%和2.5%表面粗糙度的阻力系数比较接近，在试验雷诺数范围内，阻力系数基本都小于0.8。以上结果与文献[11]中不同表面粗糙度圆柱体平均阻力系数随雷诺数的变化曲线存在差异，这是因为本研究采用的表面粗糙度相比于文献[11]的大，在试验雷诺数范围内流动已经进入高超临界区，故粗糙表面的圆柱体模型阻力系数比较稳定。

由图4可得，光滑表面的圆柱体平均升力系数在低雷诺数时近似为0，在雷诺数为25万开始增加，当雷诺数增至32万之后急剧增长，到雷诺数为36万左右达到最大值，约为1.18，之后升力系数又有减小的趋势，这与平均阻力系数变化规律是相对应的，也证实了本试验的准确性。与阻力系数类似，粗糙表面的圆柱体的平均升力系数受雷诺数的影响也较小，变化曲线十分平缓，并且粗糙度增大后平均升力系数变化不大，近似为0。

通过对不同表面粗糙度圆柱体模型阻力系数和升力系数比较分析，大致可以得出以下规律：

(1)就整体趋势而言，表面粗糙度增加，阻力系数降低。

(2)随着模型表面粗糙度增加，雷诺数相应减弱。

2.3 正多边形柱体气动力特性分析

改变柱体断面形状，分别对4种正多边形(12、16、20、24)柱体在不同风攻角下进行风洞试验，得到气动力系数随雷诺数的变化规律如图5～图8所示。

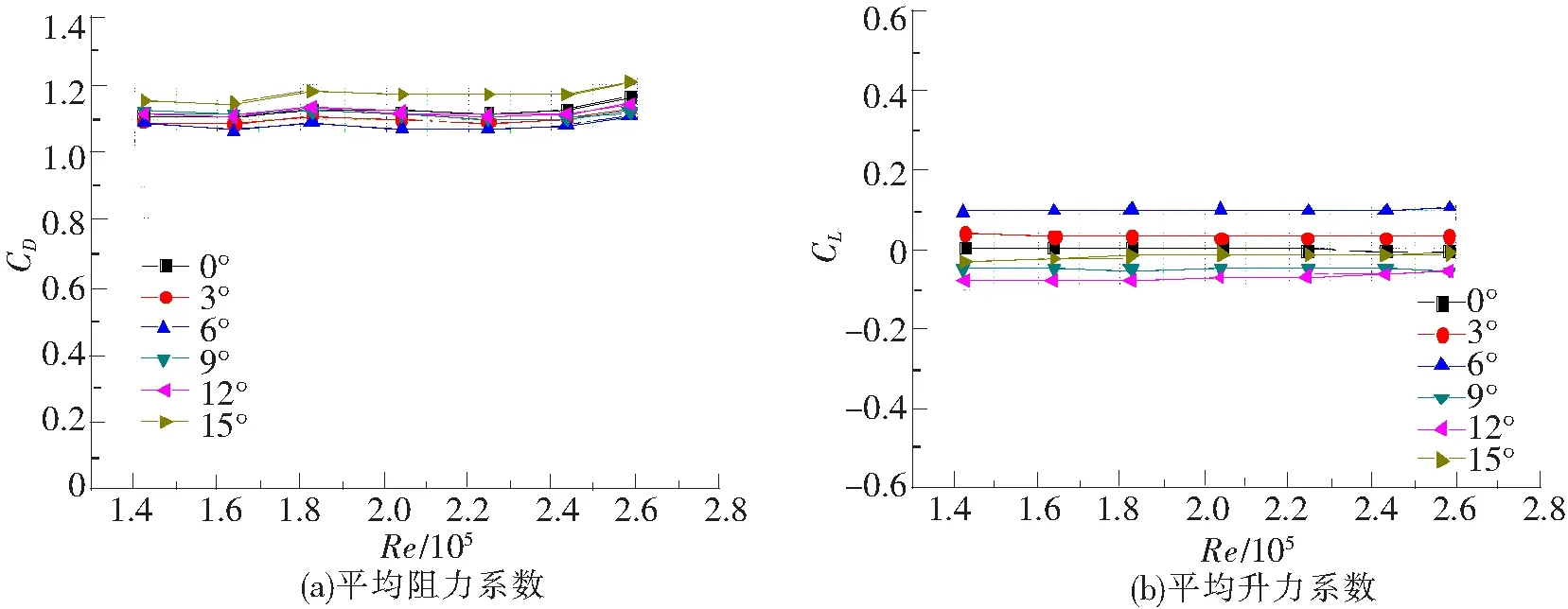
图5 正12边形柱体气动力系数随雷诺数变化

图6 正16边形柱体气动力系数随雷诺数变化

图7 正20边形柱体气动力系数随雷诺数变化

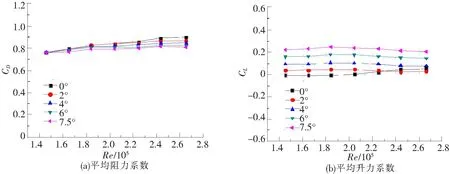
图8 正24边形柱体气动力系数随雷诺数变化

由图5～图8分析可得，在特定风攻角下，各正多边形柱体的平均阻力系数和平均升力系数基本不随雷诺数变化，曲线非常平缓；不同风攻角之间，各正多边形柱体的平均阻力系数和平均升力系数差别不大。

实际工程中，柱体结构可能承受来自各个攻角的风荷载，同时为了更方便地揭示断面边数对柱体的阻力系数与升力系数随雷诺数变化规律的影响，将同一正多边形柱体的各风攻角下气动力系数结果取平均值，以此平均值为纵坐标，雷诺数为横坐标，作出各正多边形柱体气动力系数随雷诺数变化曲线，见图9。

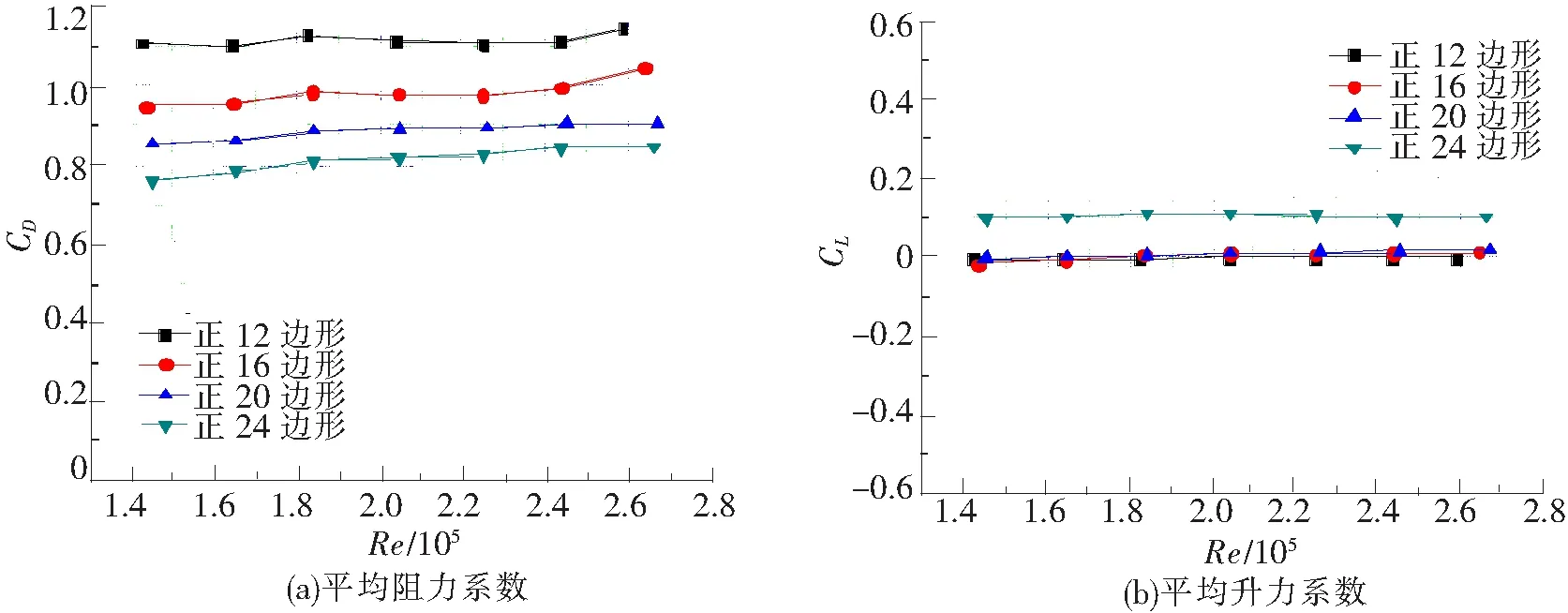
图9 各正多边形气动力系数随雷诺数变化

分析图9可得，各正多边形柱体气动力系数随雷诺数变化规律相似，但随着正多边形边数的增加，平均阻力系数有减小趋势，而平均升力系数有增大趋势。

为了工程应用的方便，结合本研究中正多边形柱体在试验雷诺数范围内的气动力系数，给出了正多边形柱体在亚临界区雷诺数范围内的平均阻力系数建议值，如表3所示。

表3 亚临界区正多边形柱体阻力系数建议值

3 结论

本研究对具有不同表面粗糙度的圆柱体和多种正多边形柱体进行风洞测力试验，分析了圆柱气动力系数与雷诺数和表面粗糙度的关系，正多边形柱体气动力受雷诺数、风攻角以及断面边数的影响，得到以下主要结论。

(1)对于圆柱体，粗糙度增加使得其平均阻力系数降低，雷诺数相应减弱。

(2)对于正多边形柱体，随着正多边形边数的增加，平均阻力系数减小，平均升力系数增大。

(3)随着风攻角的变化，正多边形柱体的阻力系数和升力系数基本保持不变。