立足基本思路，引领思路突破*——一道“希望杯”全国数学邀请赛试题的解法及变式探究

筅宁夏中卫市沙坡头区宣和镇张洪学校 张 宁

一、试题呈现

试题：（第25届 “希望杯”全国数学邀请赛初二第1试第20题）如图1，正方形ABCD的对角线AC与BD交于点O，以正方形的边BC为斜边在正方形内作Rt△BCE，∠BEC=90°.若CE=3，BE=5，则△OBE的面积是______.

从考查的知识点来看，本题以学生非常熟悉的正方形和直角三角形为基本图形，主要考查勾股定理、全等三角形的判定与性质、相似三角形的判定与性质、四点共圆的条件与性质、三角形面积的求法等知识点，这些知识点是《义务教育数学课程标准（2011年版）》规定的最基础、最核心的内容，因此，本题突出了对基础知识的考查.从核心素养角度看，本题主要考查学生逻辑推理、数学运算和直观想象的素养.本题的图形和条件简洁、明了，乍看之下感觉无从入手，经过反复思考，笔者发现本题韵味十足.从图形结构入手，立足三角形面积的基本求法，引领解题思路得以自然突破，从而得到了意想不到的收获.

二、基本思路

思路1：利用三角形的面积计算公式直接求解.

公式1：在△ABC中，设∠A、∠B、∠C的对边分别为a、b、c，三边上的高分别为ha、hb、hc，则S△ABC=aha=

公式2：在△ABC中，设∠A、∠B、∠C的对边分别为a、b、c，则S△ABC=ab sin C=ca sin B=bc sin A.

公式3：如图2，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”.由公式1易得S△ABC=ah，即三角形面积等于水平宽与铅垂高乘积的一半.

思路2：借助其他图形的面积间接求解.

可考虑借助其他图形的面积间接求解，这是一种常用的解题思路.

图2

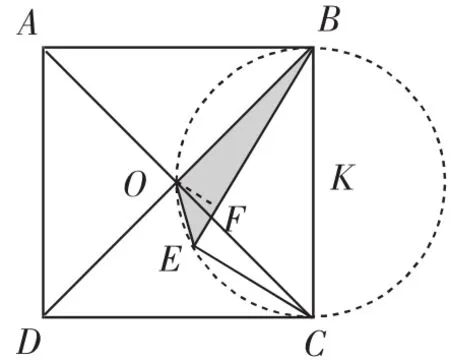
图3

三、解法探究

基于三角形的面积计算公式1，本题有如下四种解法.

解法1：如图3，设线段BC的中点为K.易知∠BOC=∠BEC=90°，所以点B、O、E、C在⊙K上.

由圆的性质，易知∠OEB=∠OCB=45°.过点O作OF⊥BE，垂足为F，则OF=EF.

令OF=x，则EF=x，BF=5-x.

易知OB2=（BE2+CE2）=17.

在Rt△BOF中，x2+（5-x）2=17，解得x1=1，x2=4（不合题意，舍去）.

所以S△OBE=BE·OF=×5×1=

点评：根据已知BE=5，欲求△OBE的面积，只需求得BE边上的高即可，故需过点O作OF⊥BE，则OF是BE边上的高，利用勾股定理易求得OF=1.这种解法立足于三角形的面积计算公式，求解思路自然、顺畅，通俗易懂，是求三角形面积的常用方法之一.

解法2：如图4，设线段BC的中点为K.易知∠BOC=∠BEC=90°，所以点B、O、E、C在⊙K上.过点E作EF⊥BD，垂足为F.由圆的性质易知∠DOE=∠BCE.

在Rt△BEF中，x2+姨2=52，即解得x1=（不合题意，舍去）.

所以S△OBE=OB·EF=×

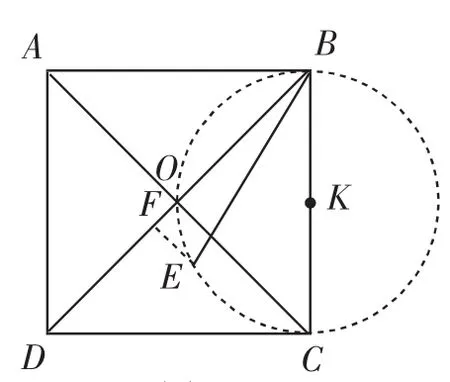
图4

图5

解法3：如图5，设线段BC的中点为K.易知∠BOC=∠BEC=90°，所以点B、O、E、C在⊙K上.分别过点B、C作OE的垂线，垂足分别为F、G.由圆的性质易知∠BEF=∠CEG=45°.

所以S△OBE=OE·BF=

点评：根据图形的特征，△BOC是等腰直角三角形，因此易联想到构造勾股定理“总统证法”中的几何图形.这种解法通俗易懂，简洁明了，充分体现了“观察—联想—转化”的求解思路，凸显了几何模型在解题中的重要作用，正所谓“心中有模型，解法自然来”.这种解法与前两种解法相比，运算量较小，过程更简洁，是一种非常优美的求解方法.

解法4：如图6，以点E为坐标原点，以CE所在直线为x轴，以BE所在直线为y轴，建立平面直角坐标系.BD与x轴相交于点F，AD与x轴相交于点G，过点D作DH⊥x轴，垂足为H.

图6

故点D的坐标为（-2，-3）.

因为点O是BD的中点，所以点O的坐标为（1，1）.

从而可知点O到BE的距离为1，所以S△OBE=×5×1=

点评：由解法1～3可以看出，求△OBE的面积的关键是求出△OBE某边上的高，即△OBE的某一顶点到对边的距离.在平面直角坐标系内，如果已知某点的坐标，那么容易得到这个点到坐标轴的距离，因此可考虑利用解析法求解本题.解析法是利用代数方法解决几何问题的一种重要方法.对于正方形、等腰三角形、直角三角形等几何图形，经过建立适当的平面直角坐标系，即可得到有关点的坐标或直线的表达式，从而将几何问题转化为代数问题，然后利用代数知识解决几何问题.解析法求解本题的不足之处是运算量较大，求解过程比较烦琐，但也是求解问题的一种方法.

基于三角形的面积计算公式2，本题有如下两种解法.

解法5：如图7，设AC与BE相交于点F.

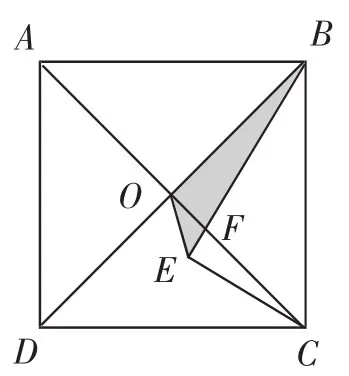
图7

在Rt△BOF中，x2+（）2=△2，即（4x-（x+4）=0，解得x1=，x=-42（不合题意，舍去）.所以CF=OC-OF=，BF=

所以S△OBE=OE·BE·sin45°=××5×

解法6：如图7，由解法5易知OB=，BF=，OF=所以sin∠OBE=

所以S△OBE=OB·BE·sin∠OBE=××5×

点评：若三角形中已知两边，且易求得这两边的夹角的正弦，则可考虑利用三角形的面积计算公式2求解，这也是求三角形面积的常用方法.求三角形内角的正弦值时，需构造直角三角形，因此以上两种解法的运算量较大，求解过程较为烦琐.

从教师的角度出发，有更简洁的方法.

解法7：如图7，令∠BCE=α，∠ACE=β，则β=α-45°.

所以sinβ=sin （α-45°）=sinαcos45°-cosαsin45°=

易知B、O、E、C四点共圆，所以sin∠OBE=sinβ=

所以S△OBE=OB·BE·sin∠OBE=

基于三角形的面积计算公式3，本题有如下解法.

解法8：如图8，过点E作EH⊥BC，过点O作OG⊥BC，垂足分别为H、G，OG交BE于点F.

由S△BCE=BC·EH=BE·CE，易知EH=

图8

故S△OBE=S△OBF+S△OEF=OF·BG+OF·GH=OF·（BG+GH）=OF·BH=

点评：公式3是一个非常有用的公式，特别是在直角坐标系中求三角形面积时具有神奇功效，能够极大地简化运算过程.

基于思路2，本题有如下两种解法.

解法9：如图9，连接DE，延长BE交CD于点F，过点E作EG⊥CD，垂足为G.

图9

所以S△EDC=CD·EG=

所以S△OBE=S△EBD=（S△BCD-S△EDC-S△BCE）=

点评：本题中，△BOE的面积不易直接求得，因此，考虑借助其他图形的面积间接求解，这里借助△BCD、△EDC、△BCE等特殊三角形的面积，间接求得了△BOE的面积，这是一种常用的解题思路.

解法10：如图10，连接DE，将△EDC绕点C沿顺时针方向旋转90°得到△E′BC.

易知S△OBE=S△ODE，四边形BE′CE是直角梯形，CE′=CE=3.

图10

所以S梯形BE′CE=（CE′+BE）·CE=12.

所以S△OBE=S△EBD=（S△BCD-S梯形BE′CE）=（17-12）=

点评：这种解法借助图形的旋转变换，将△OBE的面积问题转化为直角梯形BE′CE和直角△BCD的面积问题，求解过程简洁、明了，运算量小，是一种极为简洁的求解方法，它是本题的最优解法.笔者认为，这种解法来源于对图形结构的深刻认识，而对图形特征的深刻认识是基于解法1～9的求解过程，虽然有些解法比较烦琐甚至愚钝，但它们有利于激活解题思路，提高几何推理能力.

四、变式探究

变式：如图11，正方形ABCD的对角线AC与BD交于点O，以正方形的边BC为斜边在正方形外作Rt△BCE，∠BEC=90°，若CE=3，BE=5，则△OBE的面积是______.

图11

限于篇幅，解答从略，请有兴趣的读者自行解答.

五、结束语

关注最基础、最核心的知识，是培养学生逻辑推理核心素养的基础.《义务教育数学课程标准（2011年版）》指出，数学是人类文化的重要组成部分，数学素养是现代社会每一个公民应该具备的基本素养，并明确提出了十个关键词，即数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识，马云鹏教授认为这就是数学学科的核心素养.在数学课程中，应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想.首都师范大学的王尚志教授曾指出，学生在数学学习中应培养“数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析”这六大核心素养.推理能力是数学思维能力的重要组成部分，几何推理是培养学生推理能力的重要载体.本题所涉及的勾股定理、全等三角形的判定与性质、相似三角形的判定与性质、四点共圆的条件与性质、三角形面积的求法等知识点都是初中平面几何教学中最基础、最核心的内容.在本题求解过程中，三角形的面积计算公式引领着解题思路，实现了从“无从入手”到“一题多解”.通过这样的解题活动，能使学生领悟数学知识间的内在联系，积累数学活动经验，提高几何推理能力.