练就眼力精选好题，改编“问题”驱动教学

筅江苏省扬州市朱自清中学 余 雷

一、中国南宋著名数学家杨辉的教学思想概述

近读丁石孙、张祖贵先生著作（见参考文献［1］），其中对中国古代数学教育的阐述中，重点介绍了南宋末年的著名数学家杨辉（约13世纪中时期人，字谦光，杭州人），文中特别提到杨辉重视数学的普及教育工作，主张数学教育与学习要循序渐进，熟读审思.在数学教学上，他主张诱导学习者积极学习，从而提高计算能力；强调通过习题的演算，来领会个中奥秘，认为“好学君子，自能触类而考”，从而达到学习的要求.最为难得的是，他对做好数学习题与学习基础理论的关系，以及按什么标准选择习题有深刻的认识，强调“夫学算者，题从法取，法将题验，凡欲明一法，必设一题”“题繁难见法理，定撰小题验法理，义既通虽用繁题了然可见也”.以上数学教育原则到今天仍是十分重要的.

由以上读书笔记，笔者联想到当下数学教学领域的习题选择（即选题），本文结合近年来所见、所为、所思，谈谈课堂教学中例题与习题的选择.

二、例题与习题选编的案例分享

案例1：七年级就要重视“视为整体”的训练.

题1：已知关于x的方程x3+x=13+1的解为x=1；x3+x=23+2的解为x=2；x3+x=（-3）3+（-3）的解为x=-3.

根据以上材料，解答下列问题：

（1）观察上述方程及解的特征，直接写出关于x的方程x3+x=43+4的解为______；

（2）猜想关于x的方程x3+x=a3+a的解为______；

（3）利用（2）中猜想到的结论，求解关于x的方程（x-1）3+x=（a+1）3+a+2的解.

思路概述：前两问都可直接写出答案，第（3）问需要对方程进行整理、变形，比如，［（x-2）+1］3+［（x-2）+1］=（a+1）3+（a+1），将x-2视作一个整体，对应等式右边的整体a+1，即可得x-2=a+1，即x=a+3.

教学意图：从七年级开始就可训练学生“视为整体”的解题策略，这也是用字母表示数、列代数式之后考查较高能力水平的题型.七年级上学期教材中也经常有将“a+b”或“10m+n”看成一个整体这样的训练，而且到八年级学习乘法公式之后，就需要识别、套用公式，如将哪些部分或整体视作公式中的a或b；到九年级学习一元二次方程的求根公式、根的判别式，二次函数的图像的顶点公式，等等，都需要灵活切换视角，要有“视为整体”的眼力.

案例2：八年级几何教学要关注经典问题.

题2：【阅读回顾】教材“实验与探究”曾对三角形中边与角之间的不等关系进行研究，我们确认了以下性质：在一个三角形中，较大边（或较大角）所对的角（或边）相应也较大.简称“大边对大角”“大角对大边”.

【性质运用】（可以借助以上性质参与下列问题的推理的证明）

如图1，△ABC中，AB=AC，AD是顶角∠BAC的外角平分线，点P在射线AD上（不包括端点A），连接PC、PB.

（1）求证：PC＜PB；

（2）判断∠ABP与∠ACP的大小，并说明理由.

思路概述：（1）方法1：在△BPC中，可证出∠PBC＜∠PCB，于是BP＞CP，即获证.

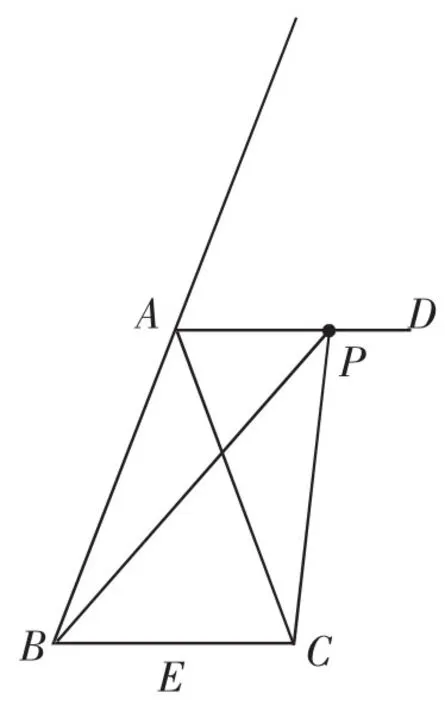
图1

图2

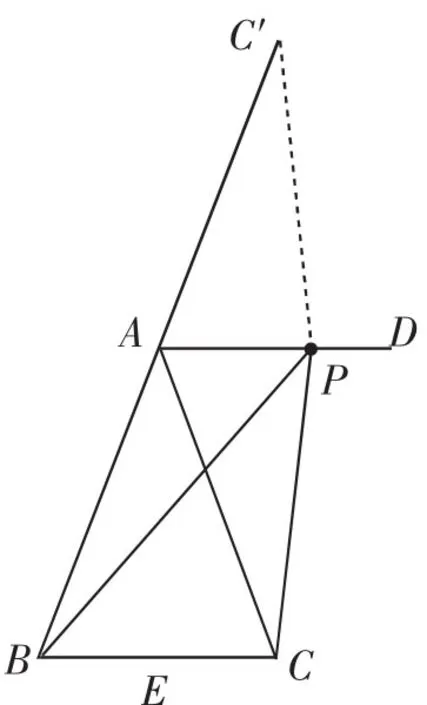
图3

方法2：如图2，作AE⊥BC于点E，交BP于点Q.在△CPQ中，CQ+PQ＞PC，而CQ=BQ，于是BQ+PQ＞CP，即获证.

（2）在BA的延长线上取AC′=AC，连接PC′.先证△APC△APC，得∠AC′P=∠ACP，PC=PC′，于是BP＞PC′.在△BPC′中，由“大边对大角”得∠ABP＜∠AC′P，问题得解.

教学意图：八年级上学期主要学习平面几何中的一些难点章节，如三角形全等、等腰三角形等特殊图形的性质，当前很多教辅资料上的这类平面几何习题盲目选用各地中考真题，加重学生学习负担，因为很多中考平面几何题都是经过图形变换之后或者是由几何画板等电脑软件动态变换之后得出的一些奇异性质，简单把这类平面几何难题“下放”在八年级上学期进行训练，学生苦不堪言，对平面几何教学产生不良导向.而像教材上经典的几何性质，如等边对等角、等角对等边，其有很大的拓展与推广空间，比如，将其“一般化”为“大边对大角”“大角对大边”，这类问题不但能训练学生做一题、会一类，使得经典问题、经典图形的教学功能得到大大提升，同时向学生传递、渗透了研究几何的方法与套路（善于从特殊走向一般）.

案例3：定长线段围平面图形的面积最大问题.

【教材习题】分别用定长为a的线段围成矩形和圆.哪种图形的面积更大？

改编习题：分别用定长为a的线段围成矩形和圆.

（1）求所围成的矩形的面积的最大值；（用含a的式子表示）

（2）哪种图形的面积更大？为什么？

思路概述：（1）设所围成的矩形的长为x，则宽为-x..S矩形=x所以当x=时（此时矩形恰为正方形），矩形面积取得最大值

（2）围成的圆面积更大，理由如下.由题意得围成的圆的半径r=S圆=πr2=因为大于矩形面积的最大值所以围成的圆面积更大.

教学意图：用定长线段围图形是小学阶段就熟悉的问题背景，而且小学时学生就积累了相关的最值经验，比如，用定长为a的线段围成的矩形中正方形的面积最大，而所有围成的平面图形中，圆的面积最大.该题在九年级教材上二次函数一章中，结论学生都记得，但是在说明理由时常常不太严谨，比如，对所围成的矩形中正方形最大缺少演算步骤，没有用二次函数解析式、配方求最值的方式.为学生设计铺垫式问题，也是积极践行杨辉数学教学思想中提出的“夫学算者，题从法取，法将题验，凡欲明一法，必设一题”.

三、关于习题选择的进一步思考

1.教师要修炼识别“好题”的专业功夫

教师需要有很多专业基本功，其中善于识别“好题”应该是一项重要的专业基本功.能从众多习题中，一眼识别那些“表述简洁、思想深刻、富有发展、解法多样”的好题确实不是一件容易的事，需要老师们在平时教学研究过程中勤于解题，归类收集，整理存档.这样坚持五年以上（甚至需要更长的时间积淀），才能对一些“好题”有较好的识别“眼力”.

2.将“好题”改编成“问题”驱动教学

在教学研究的基本问题（教什么，怎么教，教谁）中，“教什么”永远是第一位的.而数学教学离不开数学习题，要精选那些“好题”很不容易，在此基础上，还要求教师善于结合教情、学情，将好题改编成“问题”，以便运用“问题”驱动教学进程，进行所谓的“问题驱动”教学.“习题”到“问题”，一字之别，却是教学理念和教学价值观的重大转换，值得大家仔细玩味.

3.古代数学家教育智慧需要挖掘和实践

如参考文献［1］中介绍所见，中国古代数学家有很多先进的教育智慧与实践经验，值得认真学习，特别需要挖掘整理.作为一线教师，并不是数学史、中国古代数学史研究专业出身，但是可以借鉴一些文献研究中的经验，积极付诸教学实践.像本文中的识别“好题”，将“好题”改编打磨成“问题”驱动课堂教学，就可看成是践行杨辉数学教学思想的一些努力.当然，我们的实践刚起步，认识很不到位，期待更多的同行积极行动，丰富案例研究，加深我们对古代数学家的教育智慧的实践与理解.